Teória všetkého.

Definičný tvar rovnice všetkého:

κ₁ – gravitačná konštanta - 6,670.10^-11 [N.m².kg^-2]

κ₂ – rotačná konštanta - 4,934.10^-6 [kg².N^-1.s^-2]

ε – permitivita vákua - 8,854.10^-12 [F.m^-1]

µ – permeabilita vákua - 4π.10^-7 [N.A^-2]

X – vektor intenzity silnej interakcie (silného poľa) [√(m³.kg)/m².s]

Y – vektor intenzity slabej interakcie (slabého poľa) [√(kg/m³).m/s]

E – vektor intenzity elektrického poľa [N.C ^-1]

H – vektor intenzity magnetického poľa [A.m^-1]

K – vektor intenzity gravitačného poľa [N.kg^-1]

L – vektor intenzity rotácie [1.s^-1]

E_em(f)= m.c² – vzťah premeny P-hmoty na EM-hmotu
E_sb= Q.c² – vzťah premeny EM-hmoty na T-hmotu
E_P= Q.c₁² – vzťah premeny EM-hmoty na P-hmotu
E_sb= m.c₁² – vzťah premeny P-hmoty na T-hmotu
E_em(f)= m_sb.c² – vzťah premeny T-hmoty na EM-hmotu
E_P= m_sb.c₁² – vzťah premeny T-hmoty na P-hmotu

Vzorec (1) môžeme preniesť do diferenciálneho tvaru a dostaneme jeho fundamentálnejší výraz, ktorý bude vyzerať nasledovne:

Základný vzorec Teórie všetkého:

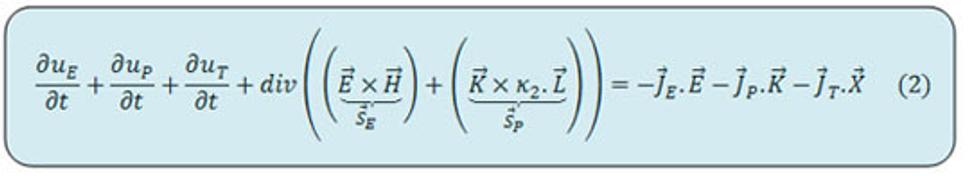
u_E = ½(ε.E.E+µ.H.H) – objemová hustota energie (EM hmoty) EM poľa [J.m^-3]

u_P = ½(K.K/4πκ₁+κ₂.L.L) – objemová hustota energie (P hmoty) priestr. poľa P [J.m^-3]

u_T = ½(X.X+Y.Y) – objemová hustota energie (T hmoty) tretieho poľa [J.m^-3]

J_E – hustota prúdu (hustota toku EM hmoty) [C.m^-2.s^-1]

J_P – hustota toku P hmoty [kg.m^-2.s^-1]

J_T – hustota toku T hmoty [sb.m^-2.s^-1]

S_E – Poyntingov vektor elektromagnetického poľa [W.m^-2]

S_P – Poyntingov vektor priestorového poľa [W.m^-2]

Kontrola fyzikálnych rozmerov:

Ostatné kontroly fyzikálnych rozmerov som uviedol v blogu – Skoncipoval som Jednotnú teóriu poľa.

Z teórie odlišnosti troch fyzikálnych polí vyplýva, že jedno z troch pohybujúcich sa fyzikálnych polí – elektromagnetické pole má svoju rýchlosť obmedzenú zhora – konštantou maximálnej rýchlosti EM poľa, fotónového svetla c). A ďalšie sa pohybujúce fyzikálne pole – priestorové pole má zase svoju rýchlosť obmedzenú zdola inou konštantou rýchlosti - konštantou najpomalšej rýchlosti c₁.

Z toho potom plynú dve relativity. Relativita Prvého fyzikálneho poľa a relativita Druhého fyzikálneho poľa. Relativitu Prvého poľa som už rozobral vo svojom predošlom blogu a ukázal tam, že takáto relativita takmer určite bude existovať a ide o závažný poznatok, ktorý rozširuje prírodovedné poznanie ľudstva.

Existuje okrem dvoch už spomenutých fyzikálnych polí ešte ďalšie fyzikálne pole – Tretie fyzikálne pole. Aká tam bude konštanta? Vzaté prísnou logikou tam nebude žiadna konštanta. Žiadne obmedzenie zdola alebo zhora pre rýchlosť. Tieto možnosti sa už vyčerpali pri predošlých dvoch poliach a pre tretie pole zvýšila iba jedná možná skutočnosť, že toto pole nemá žiadnu konštantu pre rýchlosť!

A keď tam nie je konštanta pre rýchlosť potom tam nie sú ani ďalšie konštanty, ktoré sú z tejto konštanty pre rýchlosť odvodené. Potom musíme toto tretie fyzikálne pole zapísať tak, ako to je urobené vo vzorci (1). Tam vidíme, že pred intenzitou silnej interakcie X a intenzitou slabej interakcie Y nie je žiadna konštanta.

Dokážem v tomto článku, že na opis tretieho fyzikálneho poľa neexistujú žiadne konštanty aké existujú pri opise elektromagnetického poľa alebo priestorového poľa. Urobím riadny dôkaz, ale ešte predtým sa ponorme do problematiky a preberme si ďalšie pojmy.

Vo vzorci (1) musia byť tri entity, lebo sú tri fyzikálne rozmery pre hmotnosť. Coulomby, kilogramy a silaslabóny - to sú tie tri entity. Názov pre jednu entitu – silaslabón (sb) som si vymyslel, lebo vo fyzike nie je ešte doteraz definovaná hmotnosť tretieho fyzikálneho poľa. Mohli by sme tieto hmotnosti z uvedenými fyzikálnymi rozmermi označovať aj ako m_Q[C], m_p[kg], a m_sb[sb]. Ale u m_Q zostaneme pri tradičnom, už zaužívanom výraze a to Q. U m_p (hmotnosť priestorového poľa) taktiež zostaneme pri zaužívanom m_p=m. Takže ako nové tu bude vystupovať m_sb čo je hmotnosť tretieho fyzikálneho poľa, kde jeho jednotkou je silaslabón (sb). 

Objemovú hustotu energie môžeme pozorovať ako kilogramy, ako elektricky náboj alebo ako silaslabóny - hmotnosť silnej a slabej interakcie, teda ako hmotnosť tretieho fyzikálneho poľa, T-hmoty. 

Hmotnosť má teda tri fyzikálne rozmery, ktoré sa všetky dajú vyjadriť v objemovej hustote energie. Táto spoločná fyzikálna jednotka ich zjednocuje, kde všetky interakcie je potom možné vyjadriť v jednom spoločnom výraze.

Hmotnosť tretieho poľa musíme v niečom merať. V našom prípade sme si určili, že to budú silaslabóny. Definujme si teraz intenzitu silného poľa X (silnej interakcie) v treťom fyzikálnom poli. Intenzita je defacto, že akou silou dané pole pôsobí na jednotku hmotnosti daného fyzikálneho poľa. Postupujeme rovnako ako sa postupovalo pri vyjadrení intenzity elektrického poľa alebo intenzity priestorového (gravitačného) poľa a teda aj pre intenzitu silného poľa, teda pre silnú interakciu v treťom poli budeme postupovať podobne, takže:

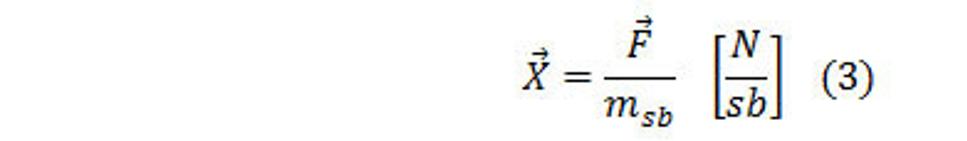
Kde

X[N/sb] – je intenzita silného poľa, silnej interakcie

F[N] – sila

m_sb[sb] – je hmotnosť tretieho fyzikálneho poľa, T-hmoty vo fyzikálnej jednotke - silaslabóny

sb – silaslabón, jednotka hmotnosti tretieho fyzikálneho poľa, T-hmoty

Nájdime teraz fyzikálny rozmer pre silaslabón – sb. Vieme, že

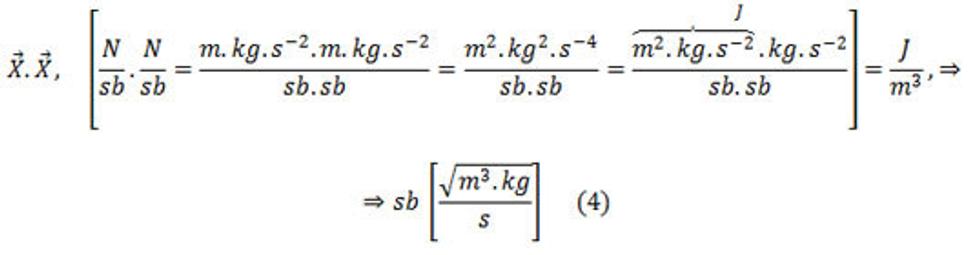
Fyzikálny rozmer silaslabónu ako jednotky pre hmotnosť m_sb tretieho fyzikálneho poľa bude v tvare (4).

Jednotka hmotnosti tretieho fyzikálneho poľa musí akoby zastúpiť aj konštantu, ktorá v treťom fyzikálnom poli nie je, aby intenzita silného poľa (silnej interakcie) násobená sama sebou dosiahla fyzikálny rozmer joule na meter kubický.

Intenzita silného poľa:

Intenzita silnej interakcie je vyjadrená podobne ako u E a K aj s podobným priebehom.

Dva body silného poľa (silnej interakcie) pôsobia na seba silou (priťahujú sa silou), ktorá sa rovná:

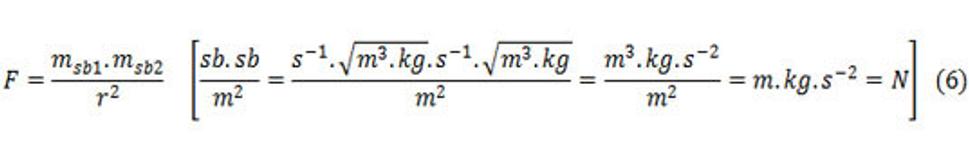
Takže, ak intenzita silnej interakcie má priebeh ako predchádzajúce dve intenzity polí – elektromagnetického a priestorového poľa, tak to nemusí byť nič zvláštne, ale práve naopak, dáva to logiku pre akúsi jednotu fyzikálnych polí s odlišnosťou ich fyzikálnych rozmerov pre hmotnosť, kde ako sme videli sú tri fyzikálne rozmery pre hmotnosť a uplatňujú sa na ne tie isté funkcie, matematické zápisy, len s výmenou fyzikálneho rozmeru pre hmotnosť.

Silná interakcia má ten istý priebeh pre intenzitu X ako ju má elektrická E alebo gravitačná sila K. Len sa urobí výmena fyzikálneho rozmeru hmotnosti a výsledok matematického zápisu zostáva rovnaký, aj keď sa tam neuplatňuje konštanta.

Je myslím zrejmé, že ak dve fyzikálne polia majú vyjadrenú svoju intenzitu poľa totožnou logikou alebo rovnakým matematickým zápisom len s vymenenými fyzikálnymi rozmermi pre hmotnosť, že to isté by mohlo alebo malo platiť aj na tretie fyzikálne pole. A platí to. Aj napriek tomu, že je tam odlišnosť a to taká, že v treťom fyzikálnom poli sa už nemôžu vyskytovať konštanty, tak aj vtedy to platí, tá logika, ktorá platila u predchádzajúcich dvoch fyzikálnych polí. Už len doriešiť Y a v podstate by táto Teória všetkého bola potom aj úplne hotová.

Interakciu Y doriešime nasledovne:

Intenzitu slabej interakcie Y budeme hľadať v tvare zlomku p/q, teda Y[p/q]. Y je vlastne nejaký ďalší fyzikálny rozmer pre rotáciu. Z predchádzajúcich dvoch polí vyplýva, že rotácia elektromagnetického poľa je vo fyzikálnom rozmere A/m ampér na meter. Rotácia priestorového poľa je 1/s teda otáčky za sekundu. Fyzikálny rozmer pre intenzitu slabej interakcie nájdeme takto:

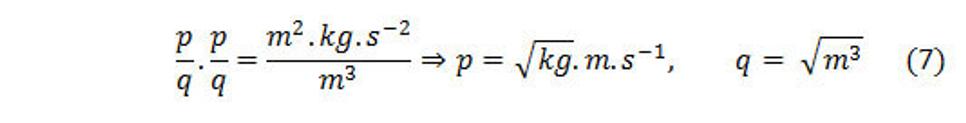
Kde p treba nejako pomenovať, je to nová fyzikálna jednotka.

A teda

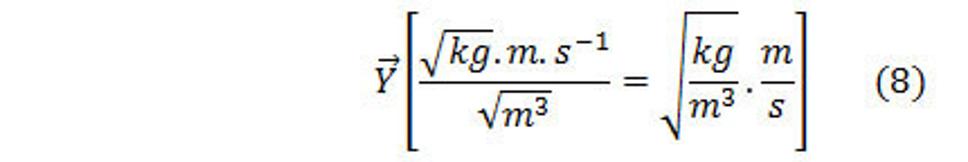
Fyzikálnym rozmerom intenzity slabej interakcie je druhá odmocnina z kg na m ³ krát meter za sekundu a je to tretí fyzikálny rozmer - rotácie.

Potom

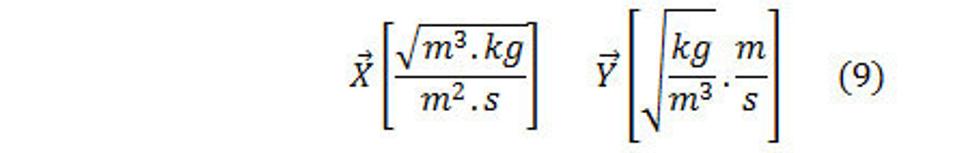
Máme fyzikálny rozmer intenzity silnej interakcie X a intenzity slabej interakcie Y. Nemáme však ešte vzťah pre Y (pre X tento vzťah máme, bol ukázaný vyššie), z ktorého nám tento fyzikálny rozmer bude vychádzať. Vidíme, že vo fyzikálnom rozmere pre Y máme m/s, čo je rýchlosť, a to napovedá, že ide o akýsi nový fyzikálny rozmer pre rotáciu a malo by to byť správne tak, ako to mám napísané. Lebo tak ako sú tri fyzikálne rozmery pre hmotnosť, tak takisto sú tri fyzikálne rozmery pre rotáciu, ktoré sú: A/m – ampér na meter, 1/s – otáčky za sekundu a druhá odmocnina z kg na m³ krát meter za sekundu. To sú teda tie tri rozmery pre rotáciu.

Z toho potom vyplýva, že nejaká elementárna častica môže rotovať v troch osiach súčasne a obyčajne z dôvodu tej ½ pred výrazom nám bude vyskakovať spin ako ½ . Sú tri fyzikálne rozmery pre rotáciu, tak záleží ako je ten spin definovaný.

Ako už bolo spomenuté - V intenzite silnej interakcie X svoju úlohu bude zohrávať slabá interakcia Y, ktorá nejakým spôsobom na silnú interakciu vplýva a vyvoláva jej priebeh taký, že od určitej vzdialenosti intenzita silnej interakcie X prudko poklesne až tak, že prestane byť úplne merateľná. Akoby išlo o dve vektorové polia, ktoré sa vzájomne odčítajú (sčítajú), až tak, že sú potom takmer na nule a to už vo veľmi malej vzdialenosti.

Preto potrebujeme nájsť ten priebeh funkcie Y. Máme zatiaľ jej fyzikálny rozmer, ale treba nám nájsť vzorec z ktorého tento fyzikálny rozmer vzniká. Teda musíme skúsiť cez nápovedu fyzikálneho rozmeru slabej interakcie Y – druhá odmocnina z kilogramu na m³ krát meter za sekundu nájsť ten vzorec. To je úloha na ďalšie dni. Potom sa porovnajú alebo dajú tieto dve polia do jedného vzťahu – sčítania alebo odčítania, alebo cez diferenciálnu charakteristiku rotácie a uvidíme čo to urobí s priebehom funkcie X, ktorý by nám mal prudko padnúť na nulu pri malom r – blízke nule. Takže toto je úloha a toto treba ešte dorobiť. Ale i napriek tomu považujem, že týmto je teória všetkého v podstate už skoncipovaná.

Ukážme si teraz ako sa dá vyjadriť úplná energia nejakej častice, ale tak, že to bude fakt úplná energia tejto častice až do tej pomyselnej bodky. Robí sa to takto:

Musíme si previesť energiu častice na jeden a ten istý typ energie (hmoty). Dajme tomu, že ju prevedieme do priestorovej interakcie. Potom

E_p= Q.c₁² + m_sb.c₁²+ ½ (K.K/4πκ₁+κ₂.L.L).V [J] (10)

Teraz keď ju prevedieme do elektromagnetickej interakcie, tak energia potom bude

E_em(f)=m.c² + m_sb.c² + ½ (ε.E.E+μ.H.H).V [J] (11)

Teraz ju prevedieme do tretieho poľa

E_sb= m.c₁² + Q.c² + ½ (X.X+Y.Y).V [J] (12)

Takto sme tromi spôsobmi vyjadrili energiu jednej a tej istej častice. Výsledky týchto troch nezávislých postupov výpočtu energie častice sa musia rovnať. Takto sa dá získať totálna energia nejakej častice, v zmysle takom, aby sme vedeli, koľko energie (hmoty) obsahuje. A toto bol postup ako sa k takému výsledku dá dopracovať.
takže

Q.c₁²+m_sb.c₁²+ ½ (K.K/4πκ₁+κ₂.L.L).V= 
= m.c² + m_sb.c² + ½ (ε.E.E+μ.H.H).V= 
= m.c₁² + Q.c² + ½ (X.X+Y.Y).V (13)

Z uvedeného vidíme, že vyjadrenie energie nejakej častice nie je až také jednoduché a má dlhší tvar zápisu ako len ten starý známy, že E=mc². Lebo tento výraz je len o množstve premenenej priestorovej hmoty na nejaké množstvo elektromagnetickej hmoty, ktoré sa deje len pri určitých fyzikálnych dejoch. Nehovorí tento Einsteinov zápis nič o celkovej energii každej častice, ktorá pozostáva z priestorového poľa, z elektromagnetického poľa a z tretieho fyzikálneho poľa. Tam sa to rieši tak, ako som už uviedol. A to je aj riešenie, ktoré patrí medzi mimozemské poznanie.

Zoberme si na úvahu výraz pre prevedenie do elektromagnetickej interakcie. Určite platí, že anihilácia hmoty prebieha výrazom, ktorý som uviedol v (11). Merania na E=m.c² boli vždy len približné. Ak sa v nejakom fyzikálnom procese premení častica obsahujúca tretie fyzikálne pole, priestorovú interakciu a elektromagnetickú hmotu, tak jej premena na čisto elektromagnetickú hmotu môže prebehnúť len podľa výrazu (11), ktorý som uviedol vyššie. Veľmi presné merania by to museli potvrdiť, že to tak je.

Dôkaz o dvoch konštantách rýchlosti pre skoncipovanie teórie všetkého. Alebo, že na opis tretieho fyzikálneho poľa už nie sú potrebné žiadne konštanty.

V poslednom vzorci pre silaslabóny už nebudú pred interakciami X a Y vystupovať konštanty. Dá sa to dokázať na základe premeny hmoty (energie) na inú formu hmoty (energie).

Predchádzajúcich odsekoch som písal, že sú tri fyzikálne polia a tie sa prostredníctvom dvoch konštánt rýchlosti vzájomne premieňajú na iné fyzikálne pole. Aby sa tri fyzikálne polia premenili navzájom medzi sebou na všetky tri fyzikálne polia cez vzťah E=mc² k tomu nám postačujú dve konštanty rýchlosti c a c₁. Dôkaz prevediem sporom.

Predpokladajme, že existuje tretia konštanta rýchlosti c₃. Potom musí platiť, že m_sb. c₃² sa premieňa na .... a to sa nedá určiť, lebo sú tam dve možnosti - buď to bude na EM-hmotu (energiu) alebo na P-hmotu (energiu). Ak by bola tretia konštanta rýchlosti, tak výraz pre premenu tretieho fyzikálneho poľa na elektromagnetickú hmotu alebo priestorovú hmotu je nevypočítateľný. Nedá sa to z tretej konštanty alebo za pomoci nej určiť. A to je spor s tým, že to má byť jednoznačný výpočet. Týmto je dokázané, že postačujú dve konštanty rýchlosti a máme jednoznačné výpočty pre všetky premeny fyzikálnych polí na iné fyzikálne pole, premeny nejakej formy hmoty (energie) na inú. Keď nie je tretia konštanta rýchlosti, nie sú z nej odvodené ani ďalšie konštanty a tie sa potom nezaobrazia ani v opise tretieho fyzikálneho poľa. Preto definičný vzorec (1) alebo aj vzorec (2) budú správne a týmto je Teória všetkého skoncipovaná.