Skoncipoval som Teóriu všetkého -Theory of everything

Dňa 1.4.2012 som napísal blog ako konspekt Teória všetkého a v ňom som sa takmer trafil do zápisu všetkých interakcií. Tento konspekt bol pre mňa veľmi užitočný a podnetný a pomohol mi trochu viac porozmýšľať o silnej a slabej interakcii. 

Rozmýšľanie prebehalo len na úrovni podvedomia a do povedomia sa to dostáva až keď mám o tom niečo napísať. I stalo sa, že keď som chcel uverejniť úplný opis Jednotnej teórie poľa, tak som potreboval napísať záverečnú stať pre túto prácu. Tam som vyjadril presvedčenie, že by som celkom určite vedel skoncipovať Teóriu všetkého a urobil som tam náčrtok pre Teóriu časticového poľa, to je teória, ktorú potrebujeme mať na Teóriu všetkého.

A celkom náhodou som tam zahrnul aj svoju podvedomú predstavu o čase, ktorú som predtým nemal dôvod zverejňovať, ale tam sa mi hodila. Napísal som, že čas je silová interakcia, z ktorej fyzikálne pole nadobúda objem. Porovnal som to cez Teóriu podobnosti a odlišnosti troch fyzikálnych polí a vyšlo mi, že jedno pole má pre časovú interakciu obmedzenie zhora a nekonečné plynutie času ďalšie pole má obmedzenie zdola a nekonečné plynutie času a pre tretie fyzikálne pole musí platiť obmedzenie zdola a aj zhora a konečné plynutie času – aby bola podobnosť a odlišnosť s ostatnými fyzikálnymi poľami.

Tak sa dostávame ku konštantám konečnosti plynutia času pre tretie fyzikálne pole. Toto keď som si uvedomil, tak som zmenil názor oproti tomu, ktorý som mal v konspekte z 1.4.2012, že tretie fyzikálne pole nie je obmedzené zhora ani zdola. Ako vidno existuje aj možnosť, že môže byť obmedzené zhora aj zdola a toto je práve tá naozajstná skutočnosť a preto teda musí platiť konečné plynutie času, čím sa vytvára časticový dojem fyzikálneho poľa, kde pre r väčšie ako je hraničná dĺžka je intenzita časticového poľa nulová, ak uvažujem, že plynutím času fyzikálne pole nadobúda objem.

Čas potom pre tretie fyzikálne pole stojí v momente ako dorazí ku konštante konečnosti plynutia času a za hraničné r už neprejde. Týmto sa nám na scénu dostávajú konštanty, ktoré musíme uplatniť pri opise tohto časticového poľa – tretieho fyzikálneho poľa.

V definičnom vzťahu budú pri interakciách silnej a slabej interakcie vystupovať konštanty rýchlosti a to rýchlosť svetla c0 a najpomalšia rýchlosť c1. Týmito dvoma konštantami opíšme časticové pole.

Keď sa pozrieme na definičný vzťah z konspektu Teórie všetkého, tak tam vystupujú pre vyjadrenie objemovej hustoty energie poľa permitivita, permeabilita, gravitačná a rotačná konštanta. Súčiny týchto konštánt nám dávajú druhé mocniny c0 a c1. V konspekte som dokázal, že žiadne ďalšie konštanty už byť nemôžu. A teda, ak chceme mať nejakú konštantu pri interakciách slabej alebo silnej interakcie, tak to jedine môžu byť druhé mocniny c0 a c1, ktoré vlastne pozostávajú z konštánt ako permitivita, permeabilita, gravitačná a rotačná konštanta.

A tak pre objemovú hustotu energie časticového poľa bude platiť:

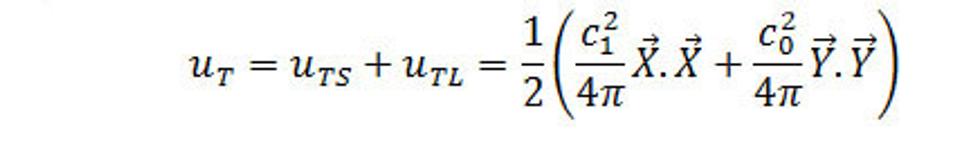
(3.)

u_T – objemová hustota energie časticového poľa
u_TS – objemová hustota energie silného poľa v časticovom (treťom) poli
u_TL – objemová hustota energie slabého poľa v časticovom (treťom) poli
X- silná interakcia silného poľa
Y – slabá interakcia slabého poľa
c1 – rýchlosť najpomalšia
c0 – rýchlosť svetla, najrýchlejšia

Teória časticového poľa.

1.Silné pole

Hustota energie silného poľa je vyjadrená vzťahom:
u_TS= c₁².X.X/4π

Odtiaľto dostaneme fyzikálne rozmery pre intenzitu silného poľa X

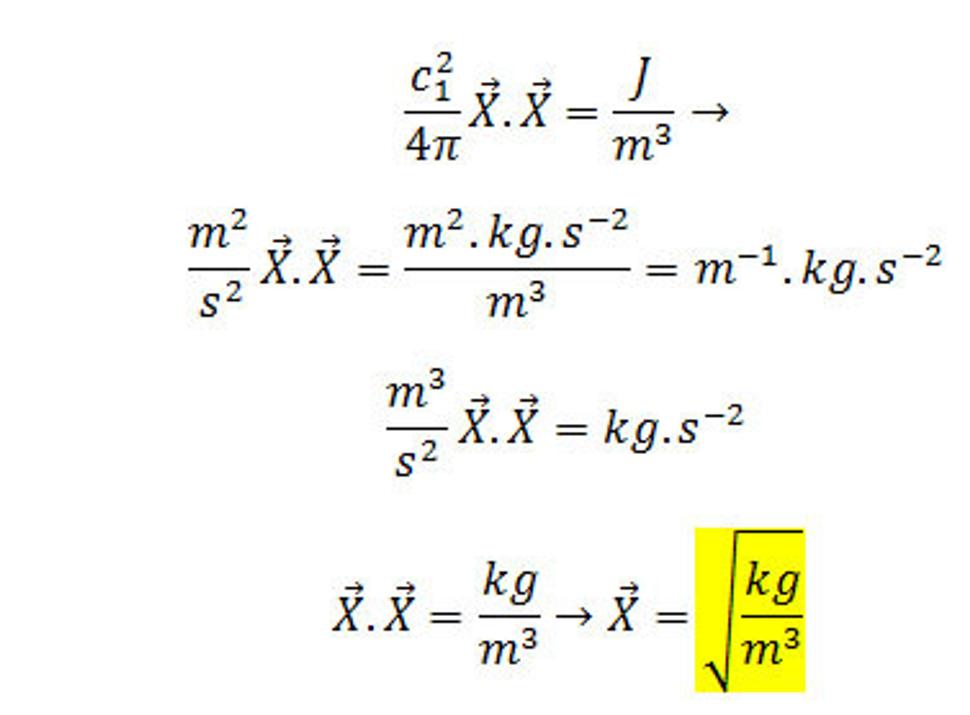
(4.)

Teraz treba vyjadriť fyzikálny rozmer pre jednotku hmotnosti časticového poľa, lebo z Teórie podobnosti a odlišnosti troch fyzikálnych polí vieme, že hmotnosť má tri fyzikálne rozmery a to kilogramy, coulomby a tretí som pracovne nazval silaslabón (sb). Tak teraz určíme fyzikálny rozmer silaslabónu. Poďme na to:

Určíme ho zo vzorca, ktorý platí pre všetky intenzity poľa všetkých troch fyzikálnych polí a hovorí to Teória podobnosti a odlišnosti troch fyzikálnych polí. Tu teda máme podobnosť v zápise s odlišnosťou vo fyzikálnych rozmeroch. Intenzita poľa sa určuje ako sila lomeno hmotnosť časti poľa v jeho príslušnom fyzikálnom rozmere pre túto hmotnosť. A tak pre intenzitu gravitácie je sila lomeno hmotnosť v kilogramoch, pre intenzitu elektrického poľa je to sila lomeno hmotnosť v coulomboch a pre intenzitu silného poľa to bude sila lomeno hmotnosť v silaslabónoch. V tomto prípade poznáme rozmer intenzity silného poľa a rozmer sily, nepoznáme len rozmer silaslabónu, ten si však z rovnice ľahko odvodíme.

(5.)

Hmotnosť tretieho fyzikálneho poľa označíme m_T. Toto pole pozostáva zo silného a slabého poľa, ktoré pôsobia svojimi silami opačne na seba a uhol, ktorý tieto sily zvierajú je nula stupňov. Obe sily na seba pôsobia a odčítavajú sa a preto musia mať rovnaky fyzikálny rozmer pre svoje intenzity poľa a preto výraz (5.) platí aj pre intenzitu slabého poľa. 

Napíšeme to v tvare:

m_T= m_TS+m_TL

kde

m_T – je hmotnosť tretieho fyzikálneho poľa vo fyzikálnom rozmere hmotnosti v silaslabónoch
m_TS – je hmotnosť silného poľa v treťom f.poli vo fyzikálnom rozmere hmotnosti v silaslabónoch
m_TL – je hmotnosť slabého poľa v treťom f.poli vo fyzikálnom rozmere hmotnosti v silaslabónoch

Zákon príťažlivej sily.

Tak ako u predchádzajúcich dvoch fyzikálnych polí – newtonov gravitačný zákon a coulombov zákon príťažlivej sily platí aj pre toto pole ten istý zákon príťažlivej sily s rovnakým zápisom, ale s výmenou konštánt a fyzikálnych rozmerov pre hmotnosť. Napíšeme si tento zákon pre silné pole.

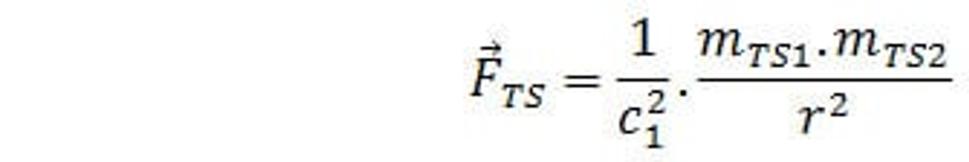
(6.)

Teraz si napíšeme tento zákon pre slabé pole.

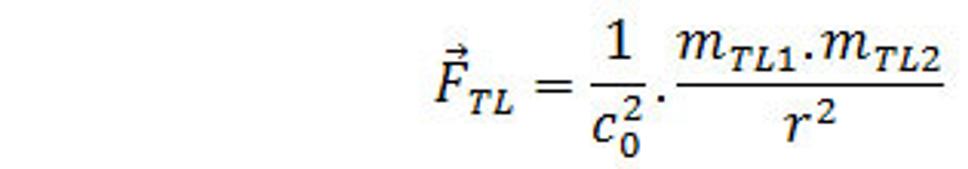
(7.)

Kontrola fyzikálnych rozmerov v rovniciach (6.) a (7.)

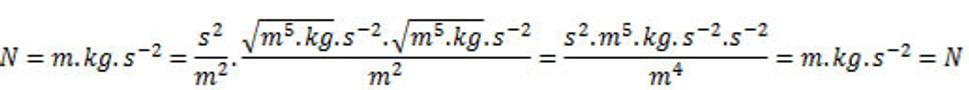
(8.)

Vidíme, že zákon príťažlivosti nám sedí vo svojich fyzikálnych rozmeroch, kde sme týmto vykonali kontrolu týchto fyzikálnych rozmerov pre daný vzorec.

Rovnica kontinuity silného poľa.

Predpokladajme, že hmota m_TS vo fyzikálnom rozmere silaslabónu je konečnej veľkosti a je rozložená v malom, ale konečnom objeme V. Hustota tejto hmoty ρ sa nazýva silaslabónová hmota uzatvorená v objemovej jednotke a môžeme ju nazývať aj hmotnostný silaslabónový náboj budiaci silnú interakciu.

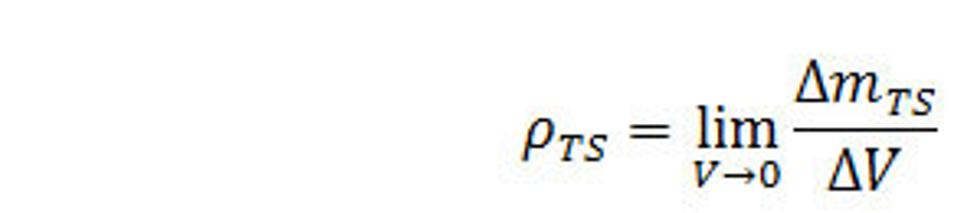
(9.)

Rozmer hustoty hmoty (hmotnostného silaslabónového náboja) je sb/m³. Hustota toku tejto hmoty (náboja) je definovaná rovnicou

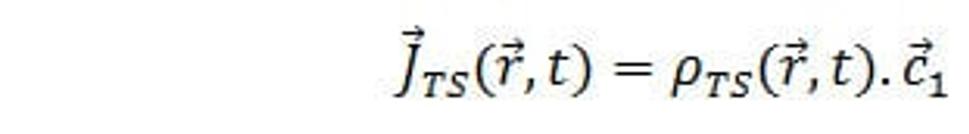
(10.)

kde c1 je rýchlosť hmotnostného silaslabónového náboja v rovnakom bode, v ktorom sa berie do úvahy hustota ρ. Rozmer hustoty hmotnostného silaslabónového náboja je sb.m².s^-1, to znamená náboj (silaslabónová hmota), ktorý(á) prejde jednotkovou plochou za jednotku času.

Hustota náboja ρ(r,t) a hustota toku silaslabónovej hmoty sú v tejto teórii časticového poľa považované za spojité funkcie polohového vektora r a času t do doby trvania konštanty konečnosti plynutia času. Pre r menšie ako táto konštanta konečnosti plynutia času nepotrebujeme uvažovať diskrétnosť náboja, to sa stane pre r väčšie ako hraničný polomer vniknutého do doby konečnosti plynutia času.

Hustota toku silaslabónovej hmoty predstavuje náboj, ktorý prejde za časovú jednotku 1 sekunda cez myslenú jednotkovú plochu kolmú na c1 v čase t, ktorá sa nachádza v mieste r. Hodnoty funkcií ρ(r,t) a J(r,t) nemôžu byť ľubovoľné, ale musia vyhovovať požiadavkám zachovania hmotnostného silaslbónového náboja.

Časová zmena náboja – (množstva silaslabónovej hmoty), ktorý(á) sa nachádza v nejakom objeme V, je definovaná pomocou derivácie

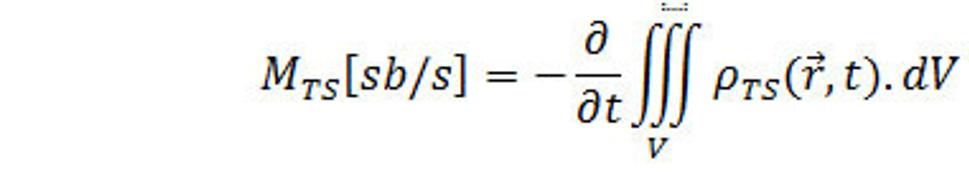
(11.)

Zmena za jednotku času sa definuje ako množstvo náboja, ktorý vytečie za tento čas z daného objemu von, alebo obrátene, vtečie do jeho vnútra. Množstvo náboja – silaslabónovej hmoty, ktoré prechádza za jednotku času cez element dS plochy S, ktorá ohraničuje náš objem sa rovná J.dS, kde hustota toku silaslabónovej hmoty v bode r, kde je element dS. Vektor dS ako obyčajne je orientovaný v smere vonkajšej normály n k ploche S, t.z. smeruje von z objemu. Preto výraz J.dS je kladný, keď náboj – silaslabónová hmota vyteká z uvažovaného objemu a je záporný keď náboj do neho vteká. Celkové množstvo náboja – silaslabónovej hmoty, ktorý vychádza za jednotku času z uvažovaného objemu je

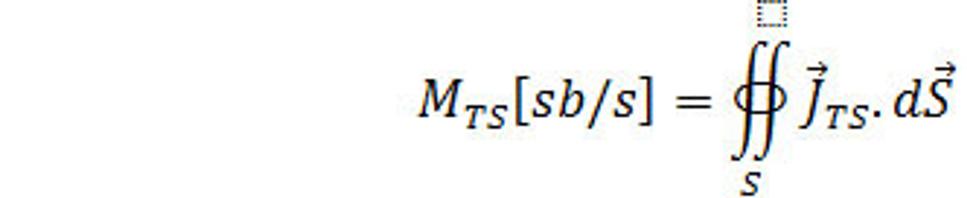
(12.)

Kde integrál sa berie po celej uzavretej ploche, ktorá ohraničuje tento objem. Musí teda platiť:

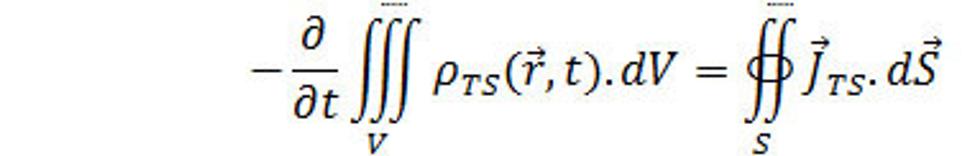
(13.)

Rovnica (13.) vyjadruje zákon zachovania náboja - silaslabónovej hmoty. Túto rovnicu teraz zapíšeme v diferenciálnom tvare. Aplikujeme na pravú stranu rovnice Gaussovú vetu, potom

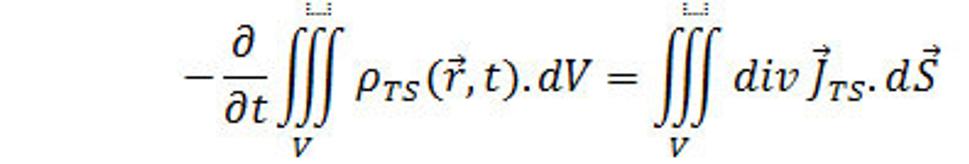
(14.)

Odtiaľ

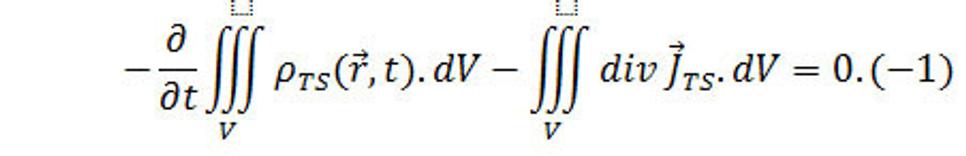
(15.)

Potom

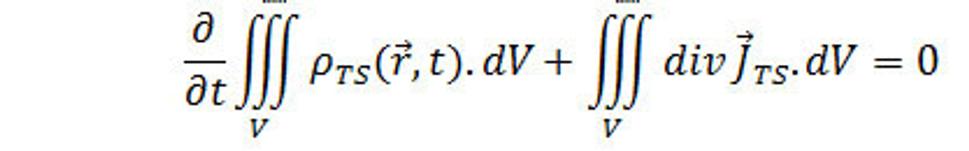
(16.)

A teda

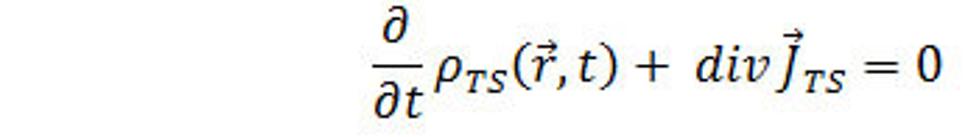
(17.)

Rovnica (17.) vyjadruje zákon zachovania silaslabónovej hmoty silného poľa v časticovom poli v diferenciálnom tvare a nazýva sa rovnica kontinuity. Obdobne sa odvodí a napíše rovnica kontinuity pre slabé pole, ktorá bude mať zápis

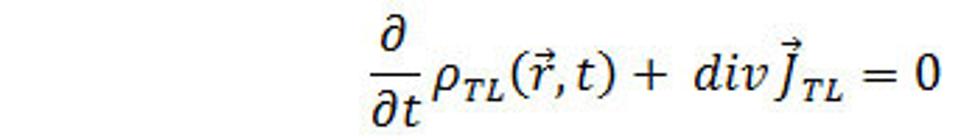
(18.)

Intenzita silného poľa, nerotácia

Silné pole je identifikované pomocou sily, ktorá pôsobí na silaslabónovú hmotu. Silaslabonová hmota je tvorená silnou a slabou interakciu, ktoré pôsobia proti sebe, čím vytvárajú jednotku hmotnosti silaslabónovej hmoty a to silaslabón. Silné pole pôsobí radiálne od povrchu gule do jej stredu, slabé pole pôsobí radiálne od stredu gule na jej povrch. Silné a slabé pole sa dá pozorovať len istou hustotou energie elektromagnetickej hmoty alebo priestorovej hmoty, preto pre niektoré elementárne častice je slabá interakcia neviditeľná, lebo nemajú v sebe správnu hustotu energie buď elektromagnetickej hmoty alebo priestorovej hmoty. Pretože silná a slabá interakcia zvierajú uhol nula stupňov, tak nebude pre toto pole žiadna rotácia a keď nie je rotácia nemôžeme uvažovať ani o kladnom alebo zápornom poli, či silného poľa alebo slabého poľa.

Nech je daný fixovaný náboj – určité množstvo silaslabónovej hmoty m_TS, ktorý vytvára vo svojom okolí časť silného poľa. Ak do tohto poľa vložíme ďalší náboj – určité množstvo silaslabónovej hmoty m_TS bude naň pôsobiť sila F_TS. Sila ktorá pôsobí na určitá množstvo silaslabónovej hmoty sa nazýva intenzita silného poľa a označujeme ju X. Všeobecne závisí na r do jej hraničnej dĺžky, ktorú prejde bod rýchlosťou c1 za čas do doby trvania konštanty konečnosti plynutia času a nezávisí na t, lebo pre tretie pole čas po určitej dobe stojí, teda neplynie, preto pri nezmenenom r a pri premennom čase výsledok bude konštantný po dobe trvania konštanty konečnosti plynutia času pre silné pole tretieho pola, uvažujeme však nekonštantný výsledok a počítame s ním len do času dokiaľ trvá a neskončila doba trvania konštanty konečnosti plynutia času pre tretie pole. Sila pôsobiaca v mieste r na určité množstvo silaslabónovej hmoty m_TS bude:

(19.)

Kontrola fyzikálnych rozmerov v rovnici (19.):

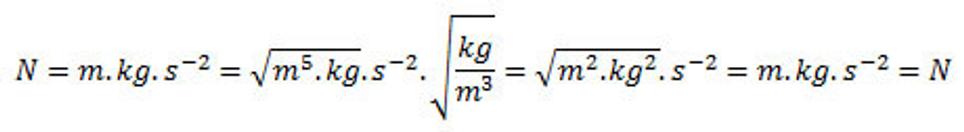
(20.)

V prípade, že silaslabónová hmota je rozložená s nejakou hustotou ρ, potom na silaslabónovú hmotu v objemovom elemente pôsobí sila

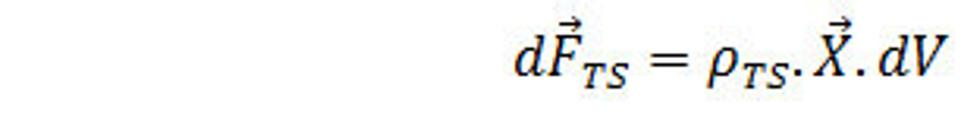
(21.)

Rovnica (19.) sa dá považovať za definičnú rovnicu silného poľa X(r,t).

V prípade, že máme spojité rozloženie silaslabónovej hmoty silného poľa s hustotou ρ, ktoré sa pohybujú rýchlosťou c1, môžeme hustotu sily (sila, ktorá pôsobí v objemovej jednotke) napísať v tvare

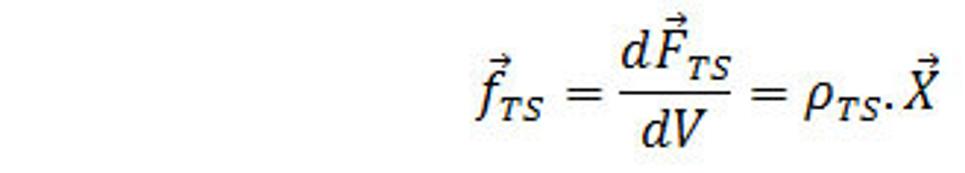
(22.)

Rovnice intenzity silného poľa.

Ak položíme určité množstvo silaslabónovej hmoty silného poľa do počiatku súradnicového systému, potom intenzita silného poľa v bode r má tvar

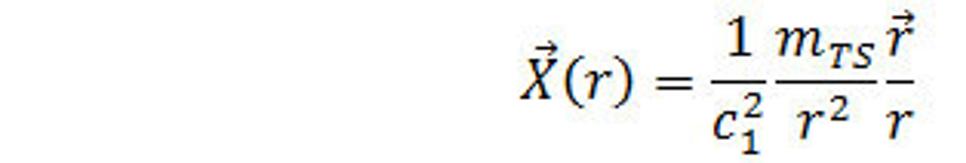
(23.)

Kontrola fyzikálnych rozmerov v rovnici (23.):

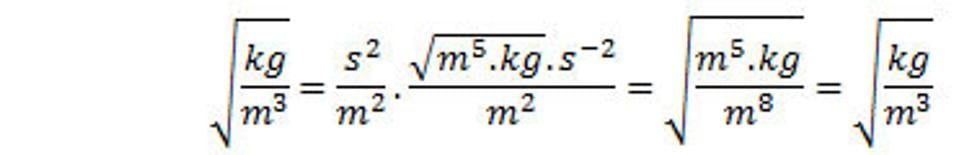
(24.)

kde r/r je jednotkový vektor v smere polohového vektora r, r=|r|. Intenzita bodového náboja má smer radiálnych lúčov. Môžeme povedať, že na povrchu gule so stredom v počiatku súradnicového systému intenzita X silného poľa má všade rovnakú hodnotu. Povrch gule s polomerom r je S=4π.r², preto

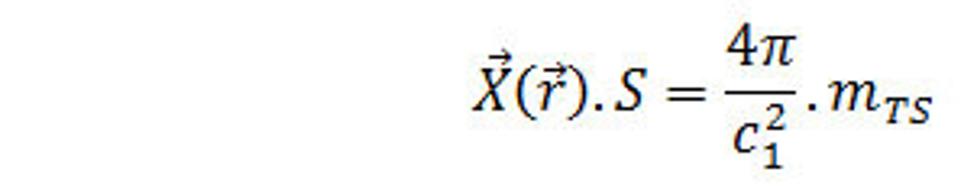
(25.)

Výraz predstavuje tok intenzity silného poľa cez uzatvorenú guľovú plochu, preto je možné tento výraz upraviť na:

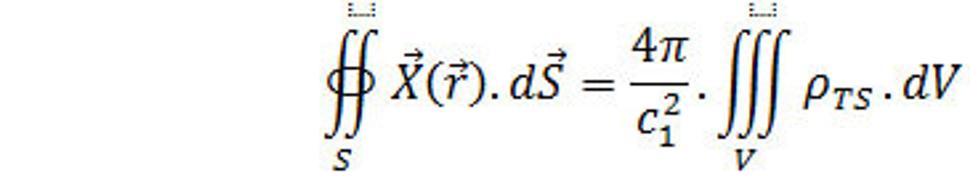
(26.)

Kontrola fyzikálnych rozmerov v rovnici (26.):

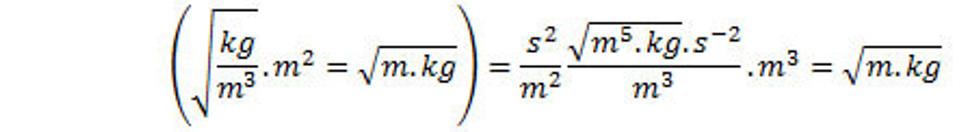
(27.)

Ľavú stranu rovnice (26.) prepíšeme na základe Gaussovej vety, potom máme

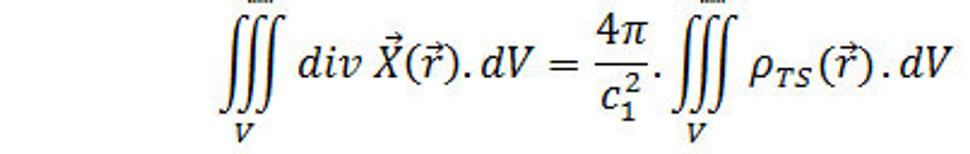
(28.)

a teda

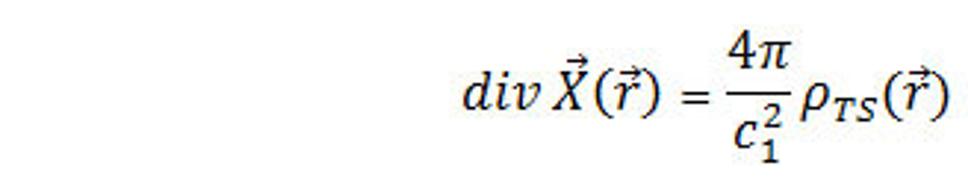
(29.)

Kontrola fyzikálnych rozmerov v rovnici (29.):

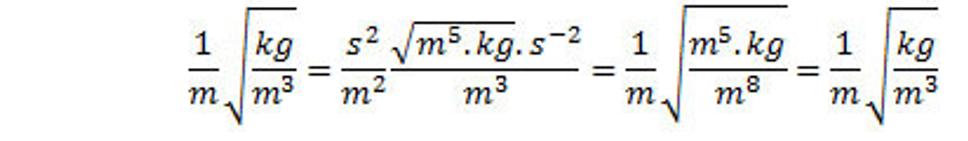
(30.)

Výraz div X si môžeme predstaviť ako tok intenzity silného poľa z jednotkového objemu. Rovnica (29.) predstavuje vzťah medzi intenzitou X a hustou ρ v tom istom mieste priestoru. Dostali sme ho ako jednoduchý dôsledok vzťahu (23.), ktorý súvisí so zákonom príťažlivosti fyzikálnych polí. Pred konštantou konečnosti plynutia času silného poľa sa X a ρ menia s časom. A teda

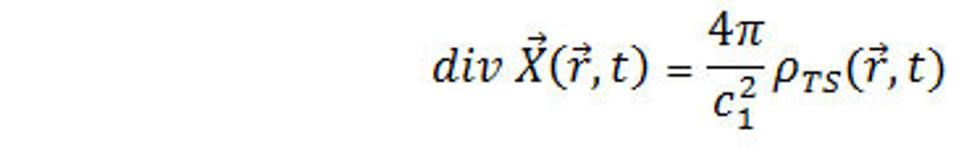
(31.)

Rovnicu (31.) teraz môžeme derivovať podľa času a potom

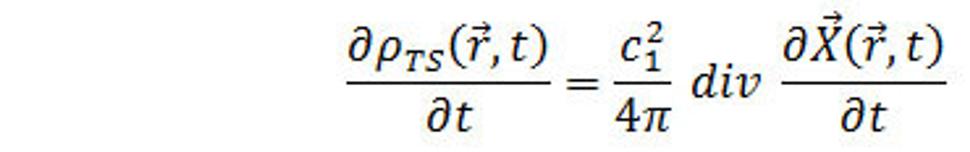
(32.)

Ak v rovnici kontinuity (17.) nahradíme časovú deriváciu hustoty silaslabónovej hmoty z rovnice (32.) dostávame

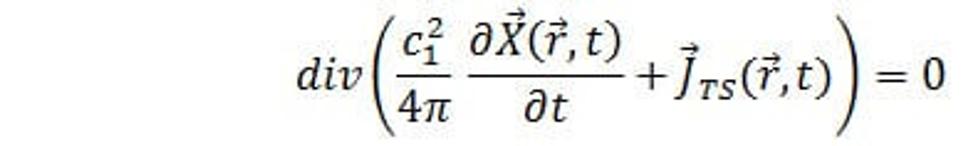
(33.)

Z rovnice (33.) potom dostávame

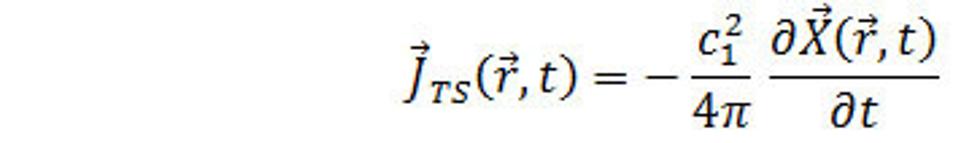
(34.)

Celkový výkon silného poľa v objeme V je určený vzťahom

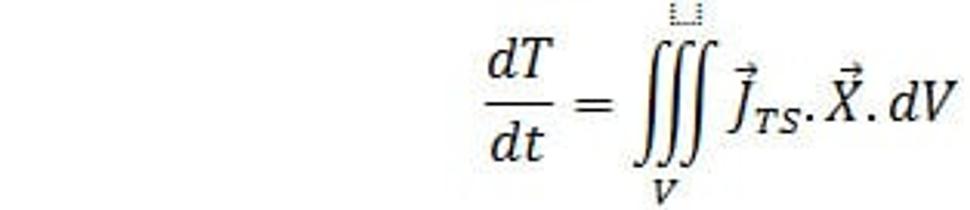
(35.)

Výraz J.X je hustota výkonu silnej interakcie. Z rovnice (34.) za J dosadíme pravú stranu do rovnice (35.) a dostaneme

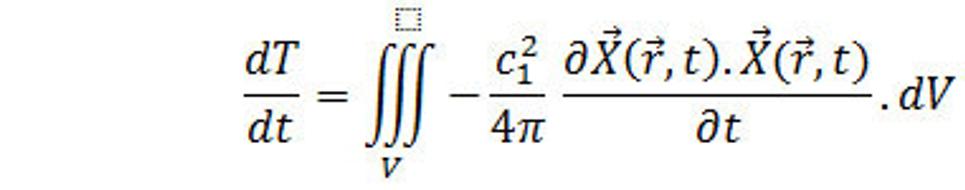
(36.)

Z toho potom

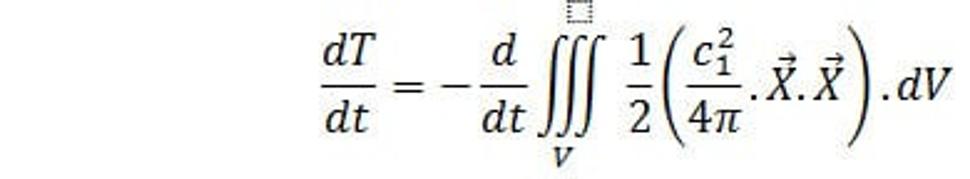
(37.)

Zo vzťahu (37.) vyplýva, že hustota energie silného poľa je

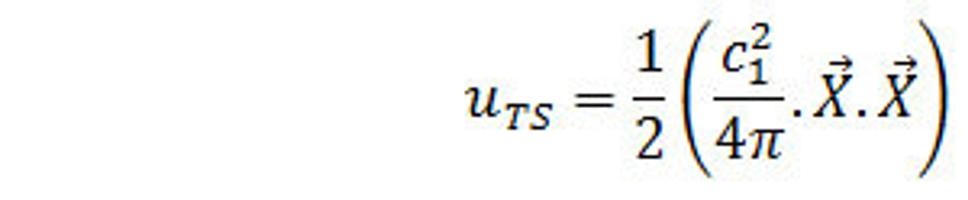
(38.)

Celkový výkon hustoty energie v objeme V je

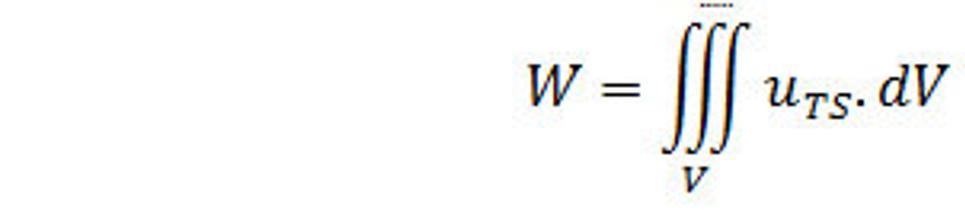
(39.)

Potom

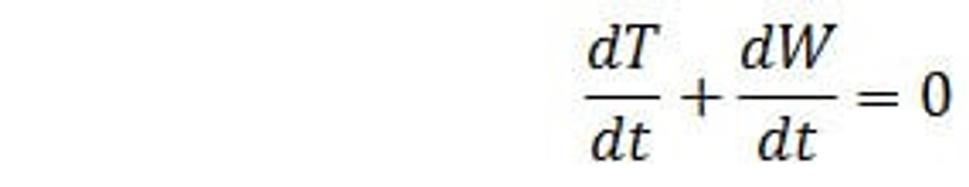
(40.)

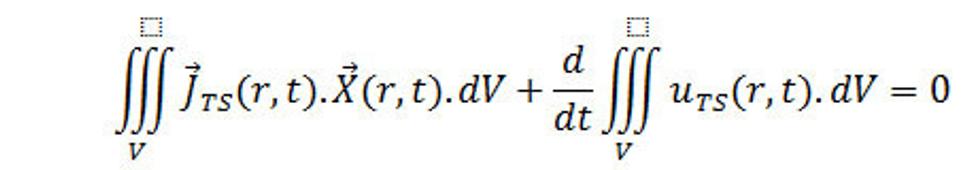
(41.)

Z čoho po úprave je

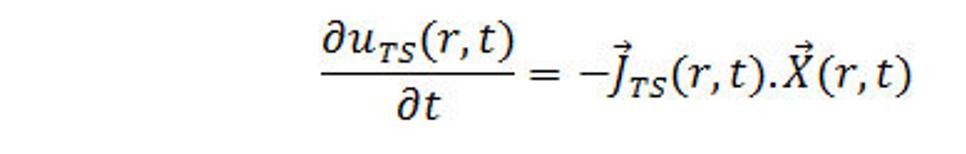
(42.)Rovnica (42.) vyjadruje zákon zachovania energie v diferenciálnom tvare pre silné pole.

Kde objemová hustota energie silného poľa je:

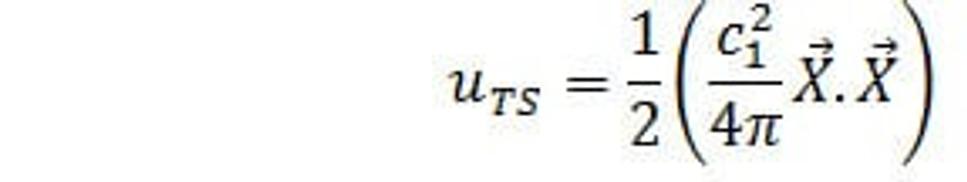
(43.)

Podobne sa odvodí rovnica (42.) výkonu objemovej hustoty energie – hustota výkonu aj pre slabé pole. Potom dostaneme pre neho:

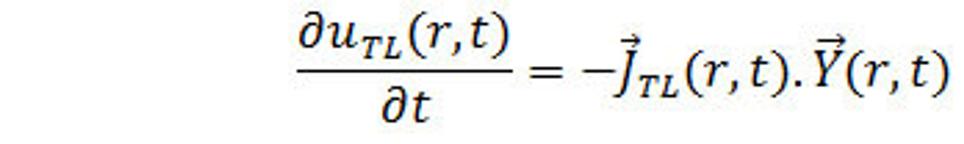
(44.)

A objemová hustota slabého poľa je

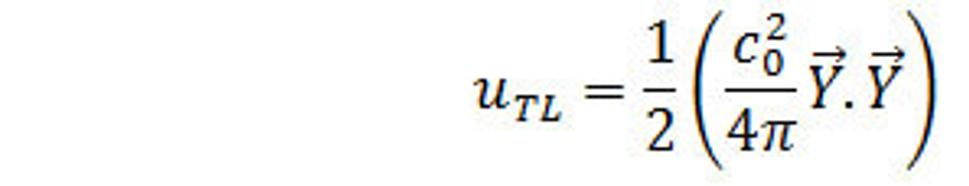
Rovnice intenzity slabého poľa.

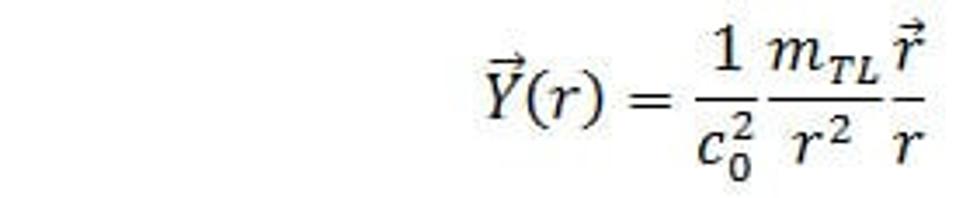
(46.)

Z rovnice (46.) podobne ako u silného poľa postupujeme a dostaneme tie isté fyzikálne zápisy ako u silného poľa, len s výmenou konštánt c1 za c0.

Definičný tvar rovnice všetkého:

(1.)

κ₁ – gravitačná konštanta - 6,670.10^-11 [N.m².kg^-2]

κ₂ – rotačná konštanta - 4,934.10^-6 [kg².N^-1.s^-2]

ε – permitivita vákua - 8,854.10^-12 [F.m^-1]

µ – permeabilita vákua - 4π.10^-7 [N.A^-2]

X – vektor intenzity silnej interakcie (silného poľa) [√(kg/m³)]

Y – vektor intenzity slabej interakcie (slabého poľa) [√(kg/m³)]

E – vektor intenzity elektrického poľa [N.C ^-1]

H – vektor intenzity magnetického poľa [A.m^-1]

K – vektor intenzity gravitačného poľa [N.kg^-1]

L – vektor intenzity rotácie [1.s^-1]

E_em(f)= m.c² – vzťah premeny P-hmoty na EM-hmotu
E_sb= Q.c² – vzťah premeny EM-hmoty na T-hmotu
E_P= Q.c₁² – vzťah premeny EM-hmoty na P-hmotu
E_sb= m.c₁² – vzťah premeny P-hmoty na T-hmotu
E_em(f)= m_sb.c² – vzťah premeny T-hmoty na EM-hmotu
E_P= m_sb.c₁² – vzťah premeny T-hmoty na P-hmotu

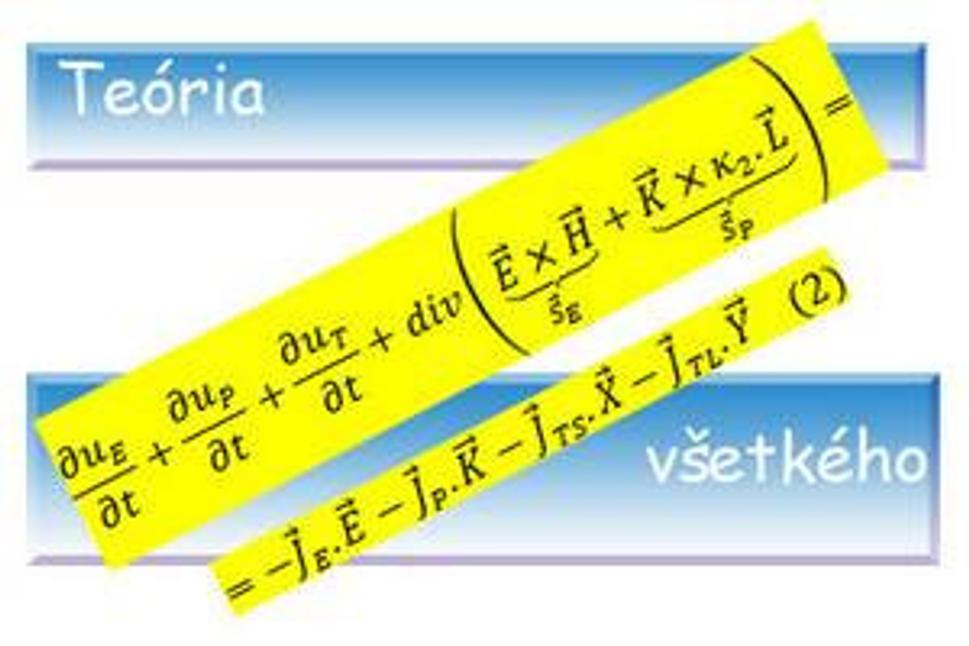
Vzorec (1) môžeme preniesť do diferenciálneho tvaru a dostaneme jeho fundamentálnejší výraz, ktorý bude vyzerať nasledovne:

Základná rovnica všetkého:

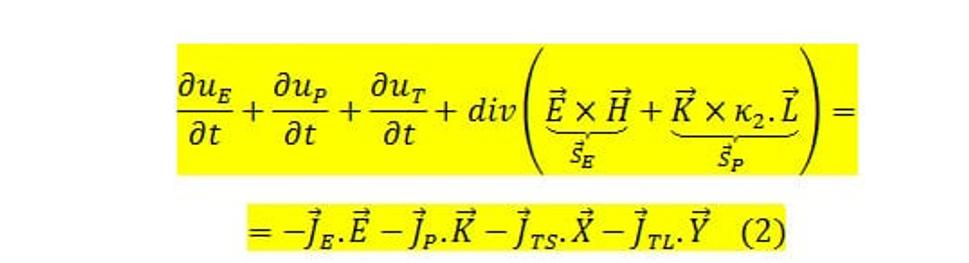
(2.)

u_E = ½(ε.E.E+µ.H.H) – objemová hustota energie (EM hmoty) EM poľa [J.m^-3]

u_P = ½(K.K/4πκ₁+κ₂.L.L) – objemová hustota energie (P hmoty) priestr. poľa P [J.m^-3]

u_T = ½(X.X.c₁²/4π+Y.Y.c²/4π ) – objemová hustota energie (T hmoty) tretieho poľa [J.m^-3]

J_E – hustota prúdu (hustota toku EM hmoty) [C.m^-2.s^-1]

J_P – hustota toku P hmoty [kg.m^-2.s^-1]

J_TS – hustota toku T hmoty silného poľa [sb.m^-2.s^-1]

J_TL – hustota toku T hmoty slabého poľa [sb.m^-2.s^-1]

S_E – Poyntingov vektor elektromagnetického poľa [W.m^-2]

S_P – Poyntingov vektor priestorového poľa [W.m^-2]

Tak toto je skoncipovaná Teória všetkého.

Mnou skoncipované teórie:

1. Jednotná teória poľa

2. Teória všetkého

3. Teória časticového poľa

4. Teória priestorovej interakcie - úplná gravitačná teória

Mnou vytvorené konspekty teórií

1. Teória podobnosti a odlišnosti troch fyzikálnych polí

2. Teória špeciálnej relativity prvého poľa - priestorovej interakcie

3. Teória kvantového javu