Unified Field Theory - Jednotná teória poľa, totálny opis - I časť.

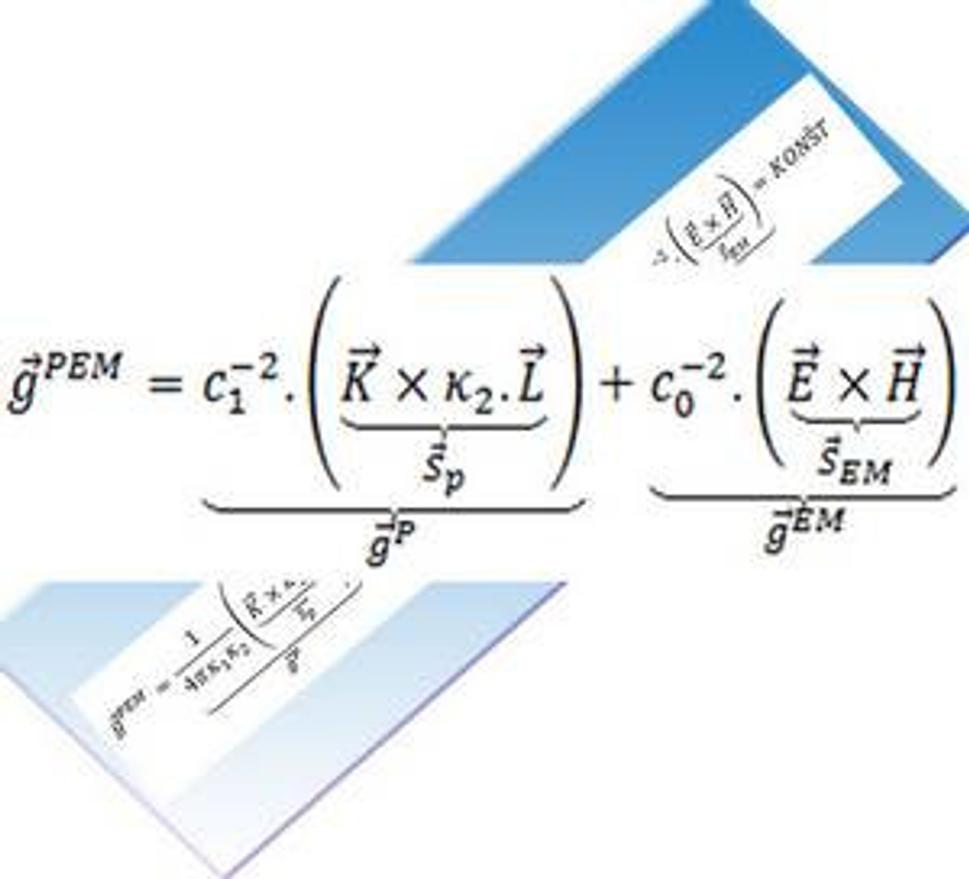
1.Interakcie. Priestorová interakcia.

Priestorová interakcia pozostáva z dvoch interakcií a to z gravitácie a rotácie, ktoré tvoria priestor. V priestore je všetka hmotnosť (kg) častíc, kde priestor je spojito rozložené hmota (kg), ktorá sa prejavuje cez dve interakcie – gravitáciu a rotáciu. Z teórie odlišnosti a podobnosti (totožnosti) troch fyzikálnych polí vieme, že existujú tri fyzikálne polia. Tretie fyzikálne pole berie do seba časť hmoty (kg) z priestorového poľa čím sa vytvára iná hustota hmoty vo vnútri tretieho fyzikálneho poľa a na túto zmenu začnú pôsobiť interakcie – gravitácia a rotácia z priestorového poľa. Takto vidíme hmotnú časticu, teleso, ktoré vnímame ako hmotnostný náboj alebo budič týchto dvoch interakcií priestorového poľa. Tie interakcie však vždy boli a vždy budú v priestorovom poli, lebo priestorové pole pôsobí cez svoje interakcie len samo na seba. Na iné polia – na ich body priestorové pole pôsobí len cez svoju hustotu energie (hmoty) nie však svojimi interakciami. V teórii priestorovej interakcie sa neskúma interakcia medzi individuálnymi hmotnými telesami, ale medzi hmotnosťou telesa – tretie fyzikálne pole zviazané časťou hmoty z priestorového poľa alebo bez tretieho fyzikálneho poľa a existujúcou priestorovou interakciou (priestorovým poľom) kde v prípade, že tam nebude tretie fyzikálne pole, tak toto pole chápeme ako spojito rozloženú hmotu – ktorá tvorí priestor, ktorej zmena hustoty priestorovej hmoty vyvolá interakcie – gravitáciu a rotáciu pôsobiace z celého priestoru na body k tejto väčšej hustote hmoty. Väčšia hustotu hmoty vzniká aj tak, že tretie fyzikálne pole sa zviaže s bodmi v priestorovom poli a pozorujeme gravitáciu a rotáciu častice. Takto získame fyzikálnu koncepciu priestorodynamiky.

V Newtonovej mechanike sa predpokladá, že rozruch sa prenáša okamžite, teda nie je potrebné pripisovať poľu hybnosť alebo energiu: akonáhle jedna z priťahujúcich častíc uvoľňuje energiu a určitú hybnosť, iná častica ich prijíma. To znamená, že v klasickej mechanike majú energiu a hybnosť len častice, ktoré na seba pôsobia. Toto sa teraz v tejto teórii priestorovej interakcii mení a energiu a hybnosť sa nebude pripisovať len hmotným časticiam ale aj celému priestoru, ktoré je taktiež fyzikálnym telesom a budeme skúmať pôsobenie tohto fyzikálneho telesa k hmotným časticiam alebo k jednotlivým hmotným bodom tohto fyzikálneho poľa – nazvaného priestor. Ešte raz priestor nie je žiadne prázdne nič ani žiadna geometria priestor tvorí spojito rozložená hmota (kg), ktorá sa prejavuje cez dve interakcie – gravitáciu a rotáciu.

Pretože priestorové pole má energiu a hybnosť, môžeme ho považovať za reálny fyzikálny objekt v takej istej miere ako hmotné telesá, ktoré pozostávajú z tretieho fyzikálneho poľa, ktoré do seba naviazali hmotu (kg) z priestorového poľa. Rovnice priestorového poľa musia priamo popisovať šírenie priestorových signálov tvoriace týmto priestor ako aj vzájomné pôsobenie hmotných telies alebo jeho hmotných bodov s týmto poľom.

Schopnosť samostatnej existencie priestorového poľa je zvlášť dobre vidieť aj z toho, že rovnice v teórii priestorového poľa pripúšťajú riešenie aj v neprítomnosti hmotných telies – telies, ktoré nie sú tretím fyzikálnym poľom. To dokazuje, že hmota (kg) je priamo v priestore a nie v treťom fyzikálnom poli, ktoré si túto hmotu (kg) iba do seba viažu a menia hustotu týchto priestorových bodov v treťom fyzikálnom poli čím sa vyvolávajú interakcie gravitácie a rotácie z fyzikálneho poľa - priestoru. Čo sa dá vysvetliť tak, že existujú tri fyzikálne polia – Teória odlišnosti troch fyzikálnych polí, kde tretie fyzikálne pole berie svoju hmotnosť z priestorového poľa. Interakcie priestorového poľa dokážu pôsobiť len a len na svoje body. Prevzatím hmoty z priestoru do seba sa tretie fyzikálne pole stáva časticou s hmotnosťou. Priestor okolo nás je spojito rozložená hmota, ktorej fyzikálny rozmer je v kg. To isté platí pre elektromagnetické pole, že je to spojito rozložená elektromagnetická hmota, ktorej fyzikálny rozmer je elektrický náboj – C. Priestorové pole sa dá opísať obdobne ako sa opisuje v klasickej teórii elektromagnetické pole, podobnosť medzi vzorcami pre výpočet gravitačnej sily dvoch telies a elektrickej sily dvoch nábojov nie je náhodná. Ide o jeden a ten istý jav iba v inom fyzikálnom rozmere. Elektrická sila je vlastne gravitačná sila, ktorá má iný fyzikálny rozmer pre svoju hmotu, podobne magnetická sila je len iný fyzikálny rozmer rotácie. Pristúpime ku vzorcom, ktorými všeobecne opíšeme priestorovú interakciu ako prejav priestorovej hmoty.

Nasledujúci opis som urobil tak, že som formálne opísal štruktúru Teórie elektromagnetického poľa a použil za elektrickú intenzitu E gravitačnú intenzitu K a za magnetickú indukciu B som dal výraz, ktorý som označil písmenom L a sú to otáčky za sekundu a je to rotácia, kde priestorové pole pozostáva z dvoch interakcií z gravitácie a rotácie, čo v následnom opise aj dokážem, že to vyhovuje tejto predstave. Lebo elektromagnetické pole a priestorové pole sú formálne totožné a líšia sa od seba len v konštantách a vo fyzikálnych rozmeroch fyzikálnych veličín, ktorými sa opisuje. Táto skutočnosť vyhovuje aj teórii odlišnosti troch fyzikálnych polí. Ďalej v opise sú použité moje opisné predstavy o priestorovom poli. V texte sa môžu vyskytovať formálne chyby vo vzorcoch, konečný pár maxwellových vzorcov pre priestorové pole by mal byť úplne správny, ale každý nadaný človek nech si to prekontroluje sám podľa nasledujúceho textu. Podstatné sú konečné výsledky. Dostávame z tohto opisu, že priestor je pole, ktoré je formálne totožné s EM poľom a dostávame na jeho opis nové konštanty, tieto konštanty sú tri a je to najpomalšia rýchlosť c1, kappa1 – gravitačná konštanta, kappa2 – rotačná konštanta. Dôležitá je tá prvá konštanta c1, ktorá hovorí o najpomalšej rýchlosti dvoch bodov priestorového poľa, na ktoré platí Iná relativita, kde ino-relativistické skladanie rýchlosti pre priestorové pole je V= (v+v´+2c1)/(1+c12/v.v´), čo znamená, že dva ľubovoľné body priestorového poľa nemôžu byť vzhľadom na seba pomalšie ako je c1. V závere to c1 ukážem aká je jeho hodnota a ako som ju vypočítal, taktiež ukážem ako som vypočítal ostatné konštanty. Takže tento opis priestorovej interakcie je úplný v tomto blogu. C1-rýchlosť priestorónu je ohraničenie zdola oproti ohraničeniu z hora pri c0-rýchlosť fotónu, ktoré sa rovná rýchlosti svetla. Rýchlosť svetla označujem c0, najpomalšiu rýchlosť označujem c1. Body priestorového poľa nemôžu byť pomalšie ako c1. Zhora obmedzenie nemajú. A c1 bude figurovať v opise priestorového poľa. V priestorovom poli sa dva body voči sebe navzájom nemôžu pohybovať pomalšie ako je rýchlosť c1, ani osobitne nemôžu byť pomalšie ako je rýchlosť c1, kde c1 je univerzálna prírodná konštanta akou je aj rýchlosť svetla c0.

2.Zákon zachovania hmotnosti (hmoty, energie). Rovnica kontinuity.

Aby sme mohli formulovať rovnice priestorového poľa, potrebujeme si zaviesť pojem hustota priestorovej hmoty a hustota toku priestorovej hmoty.

Predpokladajme, že máme iba malú objemovú časť hmotnosti (hmoty) priestorového poľa bez zlúčenia s tretím fyzikálnym poľom o konečnej hmotnosti Δm rozloženú v malom ale konečnom objeme ΔV. Hustota hmoty ρ sa nazýva množstvo priestorovej hmoty uzavretej v objemovej jednotke.

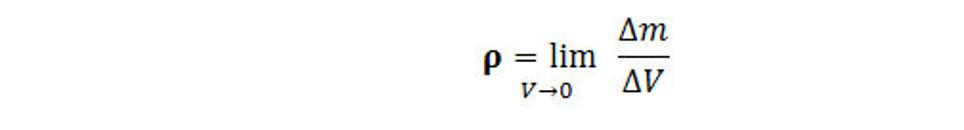
Rozmer hustoty priestorovej hmoty pre objem je kg.m^-3.

Hustota toku priestorovej hmoty je definovaná rovnicou

Kde v je rýchlosť hmoty v rovnakom bode, v ktorom sa berie do úvahy jej hustota ρ. Rozmer hustoty toku hmoty J je kg.m^-2.s^-1, to znamená množstvo hmoty, ktoré prejde jednotkovou plochou za jednotku času.

Uvedené fyzikálne veličiny ako sú hustota hmoty a hustota toku hmoty sú potrebné na vyjadrenie rovníc pre opis priestorového poľa. Preto tu bol uvedený tento ich fyzikálny opis.

Hustota priestorovej hmoty ρ(r,t) a hustota toku priestorovej hmoty J(r,t)[kg.m^-2.s^-1] budeme v teórií priestorového poľa považovať za spojité funkcie polohového vektora r a času t a v skutočnosti sú aj spojité tieto fyzikálne veličiny. Matematika je v tomto prípade priamou prírodovedou. Dokazuje to kvantová veta. Sú preto spojité, lebo priestor je spojito rozložená hmota a svoj časticový rozmer dostáva spojením s tretím fyzikálnym poľom, ktorý v priestore nadobúda súradnice polohy r.

Hustota toku hmoty predstavuje priestorovú hmotu, ktorá prejde za časovú jednotku (1 sekunda) cez myslenú jednotkovú plochu kolmú na rýchlosť v v čase t, ktorá sa nachádza v mieste r. Hodnoty funkcií ρ(r,t) a J(r,t) nemôžu byť ľubovoľné, ale musia vyhovovať požiadavkám zákona zachovania hmoty (energie), hmotnosti priestorového poľa.

Časová zmena množstva hmoty, ktoré sa nachádza v nejakom objeme, je definovaná pomocou derivácie

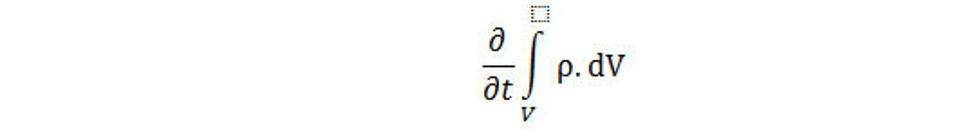
Zmena za jednotku času sa definuje ako množstvo priestorovej hmoty, ktorá vytečie za tento čas z daného objemu von, alebo obrátene, vtečie do jeho vnútra. Množstvo hmoty, ktoré prechádza za jednotku času cez element dS plochy S, ktorá ohraničuje náš objem sa rovná J.dS, čo je hustota toku priestorovej hmoty v bode r, kde je element dS. Vektor dS je orientovaný v smere vonkajšej normály n k ploche S, tzn. Smeruje von z objemu. Preto výraz J.dS je kladný, keď priestorová hmota vyteká z uvažovaného objemu a je záporný, keď priestorová hmota do neho vteká. Celkové množstvo priestorovej hmoty, ktorá vychádza za jednotku času z uvažovaného objemu je

kde M je množstvo pretečenej hmoty cez plochu S za jednotku času a jej fyzikálny rozmer je M(kg.s^-1) a integrál sa berie po celej uzavretej ploche, ktorá ohraničuje tento objem. Musí teda platiť

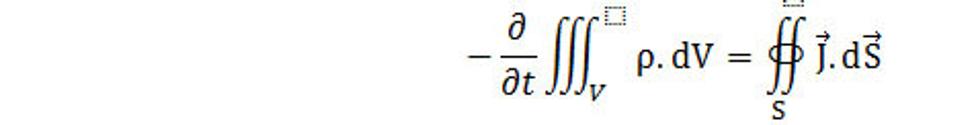
Rovnica vyjadruje zákon zachovania priestorovej hmoty. Túto rovnicu môžeme zapísať v diferenciálnom tvare. Aplikujeme na pravú stranu rovnice Gaussovú vetu, potom

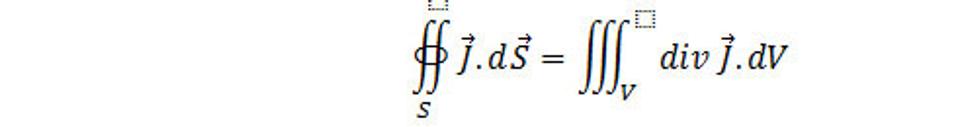
Z rovníc nájdeme, že

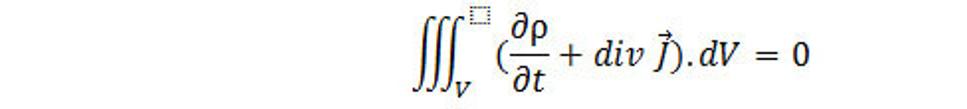
Táto rovnica platí pre ľubovoľný objem, cez ktorý integrujeme, preto sa integrand musí rovnať nule. A teda

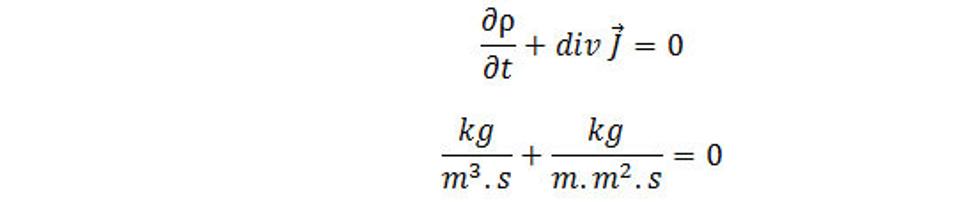
Rovnica vyjadruje zákon zachovania priestorovej hmoty v diferenciálnom tvare a nazýva sa rovnica kontinuity. Fyzikálny rozmer ρ je kg.m^-3, ρ[kg.m^-3], fyzikálny rozmer J je kg.m^-2.s^-1, J[kg.m^-2.s^-1].

3. Intenzita gravitačnej sily a rotácia priestorovej hmoty.

Priestorové pole je identifikované pomocou síl, ktoré pôsobia na jednotlivé body spojito rozloženej priestorovej hmoty, teda tieto sily pôsobia iba na body tej hmoty, z ktorej sú vytvorené alebo to možno povedať aj opačne, že hmotu tvoria práve tieto sily. V prírode existujú dva druhy hmotných bodov priestorovej hmoty, kladné a záporné. Kladné a záporné body sú nielen rozlíšiteľné, ale aj oddeliteľné. Preto celkový priestor, ktorý nás obklopuje má len jeden pól a ďalšie póly sú identifikovateľné až pri elementárnych časticiach, nejaké antisvety vo vesmíre neexistujú, celý kozmos je priestor s jedným a teda s rovnakým pólom, čo znamená, že celý vesmír pozostáva z hmoty, kde antihmota sa vo vesmíre netvorí do antihviezd, antiplanét a podobne, nič také neexistuje. Antihmota existuje len na mikroskopickej úrovni a znamená to len toľko, že body tohto priestorového poľa sa točia opačne ako body celého kozmu, vesmíru, ktoré je jedným veľkým fyzikálnym poľom priestorovej hmoty s rovnakým točením svojich bodov, z ktorých toto pole pozostáva. Ak sa tieto body zviažu s tretím fyzikálny poľom tak sa môže stať, že nastane zmena rotácie z dôvodu pôsobenia vonkajších síl, ktoré zmenia polaritu otáčania tretieho fyzikálneho poľa, ktoré je časticou.

Majme fixované tretie fyzikálne pole, ktoré do seba naviazalo priestorovú hmotnosť Δm, ktorá svojou hustotou ρ vyvolá vo svojom okolí gravitačné pole, čo znamená, že všetky okolité body získajú na seba vektor sily pôsobiacej do miesta, v ktorom je väčšia hustota priestorovej hmoty. Ak do tohto poľa vložíme ďalšie tretie fyzikálne pole so zviazanými bodmi priestorovej hmoty, tak bude na toto tretie fyzikálne pole pôsobiť sila F_g. Sila, ktorá pôsobí na hustejšie priestorové body v treťom fyzikálnom poli sa nazýva gravitačná intenzita a označíme ju ako K. Všeobecne závisí od premenných r a t. Sila pôsobiaca v mieste r a v čase t na tretie fyzikálne pole s viazanými hustejšími priestorovými bodmi bude

V prípade, že tretie fyzikálne pole s nejakou hustotou priestorovej hmoty ρ[kg/m3] je s ďalšími tretími fyzikálnymi poliami rozložené v objemovom elemente dV, potom na priestorové body vo vybranom treťom fyzikálnom poli pôsobí sila

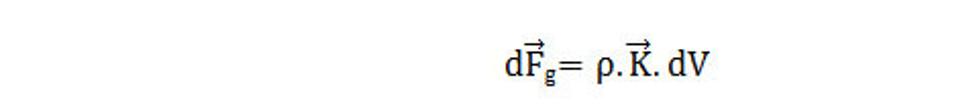
Teraz potrebujeme definovať rotačnú silu. Budeme postupovať nasledovne. Predpokladajme, že priestorové body tečú v nejakej malej objemovej jednotke dV vzhľadom na ostané body nejakým smerom a s rýchlosťou v. Pohybujúci sa element dV nám dovolí pozorovať rotáciu L, ktorá je nerozlučne spojená s hmotnými bodmi priestoru. Táto sila rotácie sa líši svojim silovým pôsobením od intenzity gravitačného poľa. Treba si predstaviť ten element dV ako guľu, ktorá rotuje. Ak túto guľu vrhnete nejakou silou na nejakú plochu tak sa začne guľa valiť priamočiarym pohybom, z ktorého ho bude vychyľovať rotačná sila v závislosti od toho ako bude postavená rotačná os pri gúľaní sa tohto elementu dV po ploche. Budeme pozorovať, že guľa z priamočiareho pohybu sa dostáva do krivkového pohybu, že ju z priamej dráhy vychyľuje nejaká sila. A to je tá rotačná sila. Na ľubovoľný bod priestoru pôsobí sila rotácie, ktorú môžeme vyjadriť takto

kde F_r[N] je rotačná sila, ktorá pôsobí na bod priestorového poľa v silnejšej hustote bodov priestoru, m[kg] je hmotnosť elementu bodov priestoru, v[m.s^-1] je rýchlosť elementu bodov priestoru. L je rotácia a jej fyzikálny rozmer sú otáčky za sekundu čo sa zapisuje ako 1/s teda L[1.s^-1].

Sčítaním rovníc dostaneme

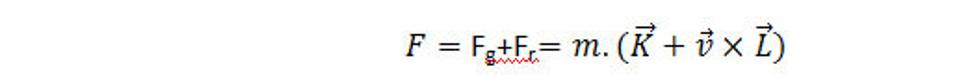
Sila F[N] sa nazýva Lorentzová sila. V prípade, že máme spojité rozloženie priestorovej hmoty v elemente dV s hustotou ρ[kg.m^-3], ktoré sa pohybujú s rýchlosťou v[m.s^-1], môžeme hustotu sily (sila, ktorá pôsobí v objemovej jednotke) napísať v tvare

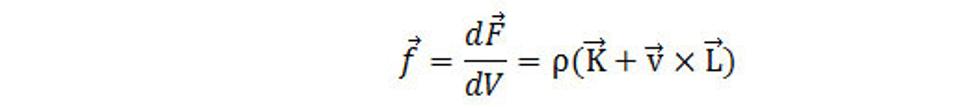
Maxwellové rovnice:

4. Prvý pár Maxwellových rovníc.

Predpokladajme, že máme karteziánsky súradnicová systém. Body trojrozmerného fyzikálneho priestoru, ktorý nie je žiadnou geometriou, ale fyzikálnym poľom budeme pre tento prípad uvažovať ako totožné s bodmi trojrozmerného euklidovského priestoru – ktorý je abstrakciou, ale odpovedá však fyzikálnej skutočnosti, ktorá má matematické vyjadrenie. Toto sa bude vzťahovať aj na ďalší matematický aparát v nasledujúcich kapitolách.

Prvý kvantitatívny zákon v teórii gravitačného poľa bol Newtonov gravitačný zákon intenzity gravitačného poľa hmotného telesa m(kg). Ak položíme hmotnosť telesa m do počiatku súradnicového systému, potom intenzita gravitačného poľa v bode r má tvar

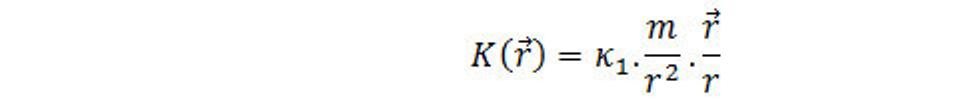
Kde r/r je jednotkový vektor v smere polohového vektora r, r= |r|. κ₁ je gravitačná konštanta. Intenzita gravitačnej sily elementu ΔV hustejších bodov priestorového poľa má smer radiálnych lúčov.

Na povrchu gule so stredom v počiatku súradnicového systému intenzita K má všade rovnakú hodnotu. Povrch gule s polomerom r je S=4πr², preto

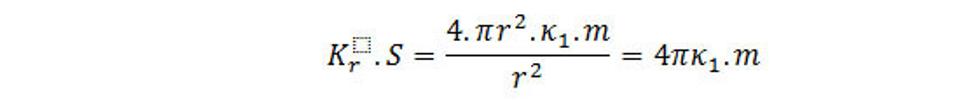
Tento výraz predstavuje tok intenzity gravitačného poľa z bodového elementu dV s väčšou hustotou priestorovej hmoty (hmotných bodov) priestorovej interakcie v tomto elemente dV cez guľovú plochu.

Teraz sa obrátime na všeobecnejšiu úlohu, ktorá súvisí s fyzikálnou úvahou, dotýkajúcou sa toku intenzity gravitačného poľa.

Nech v je rýchlosť stacionárneho prúdenia nestlačiteľnej kvapaliny. Daná je časť povrchu S, potom má zmysel hovoriť o veličine, ktorá predstavuje tok kvapaliny, ktorý prechádza cez S za jednotku času.

Ak S je nejaký malý orientovaný kúsok, potom v je konštantné a blízko k S. Tok kvapaliny, ktorý prechádza cez S za jednotku času je vyjadrený množstvom kvapaliny, ktorá je obsiahnutá v hranole (rovnobežnostene) na obr. č.1, n je vektor jednotkovej normály ku S. Teda, tok cez S je rovný objemu tohto telesa. Je zrejmé, že sa rovná (v.n)×S.

Ak aproximujeme ľubovoľnú orientovanú plochu S pomocou polygonálnych plôch a vypočítame tok cez polygonálne plochy pomocou predchádzajúceho vzorca, dostaneme, že tok cez plochu S je

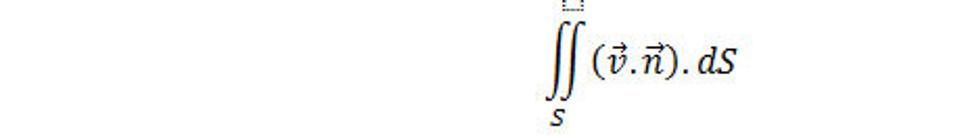
Kde n je jednotková normála ku S a dS je element plochy. Pre bodový objemový element priestorovej hmoty, ktorého vyššia hustota hmoty ako jeho okolia vyvoláva vo svojom okolí gravitačnú interakciu a platí, že divergencia tejto gravitačnej intenzity sa rovná nule

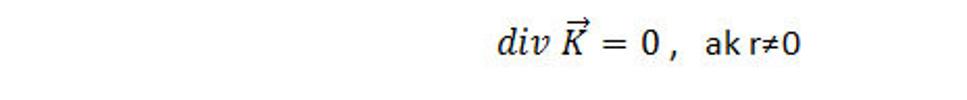
Skutočne, pre

Pričom x1, x2, x3 sú komponenty vektora r , K má zložky

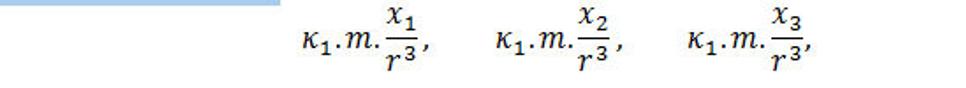
Takže

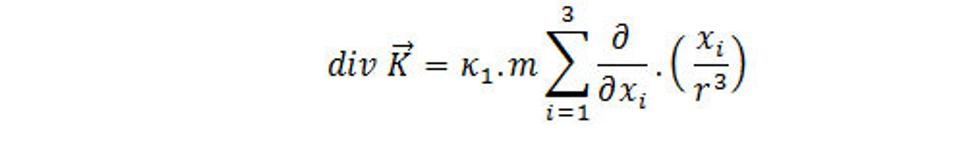
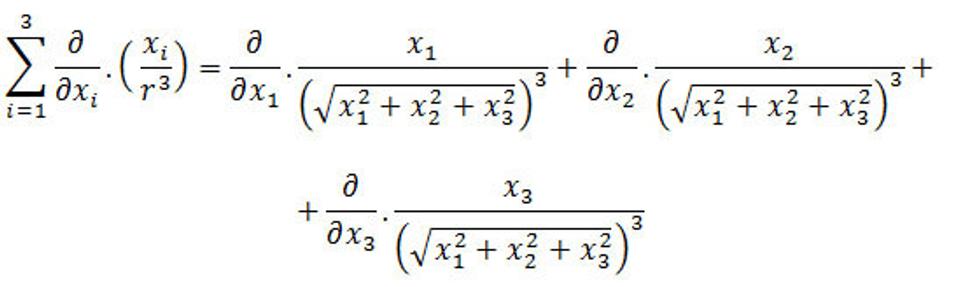
Platí, že

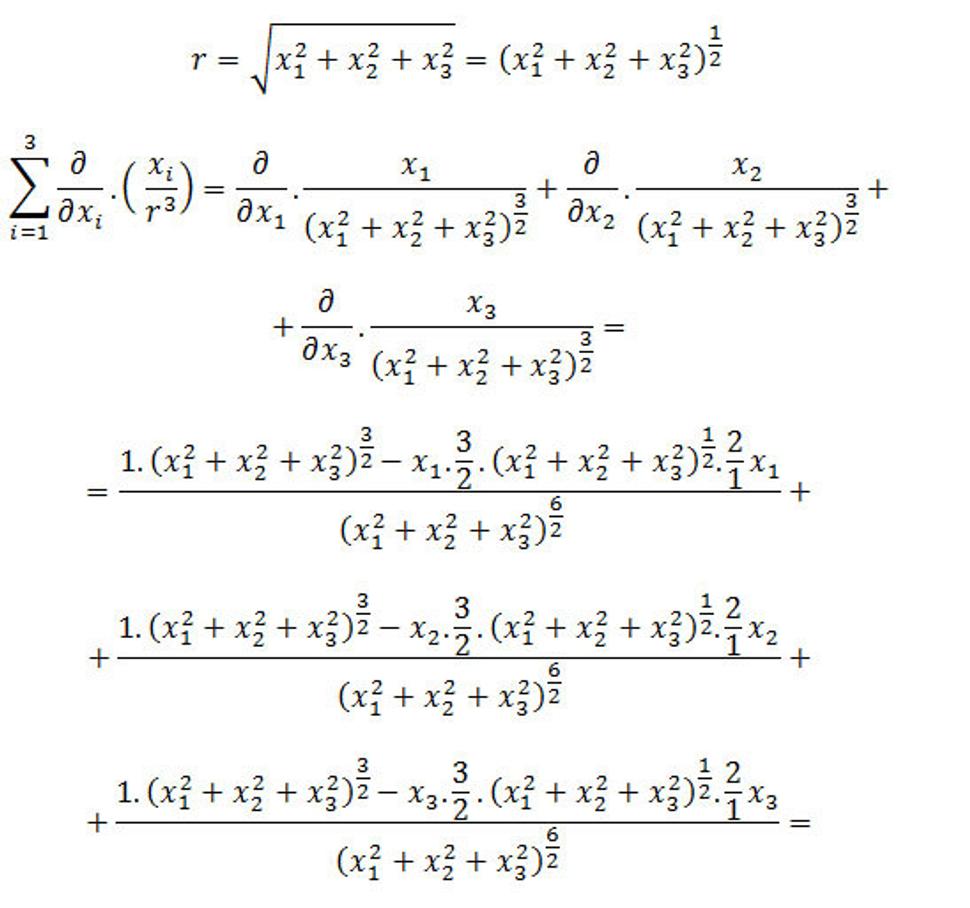
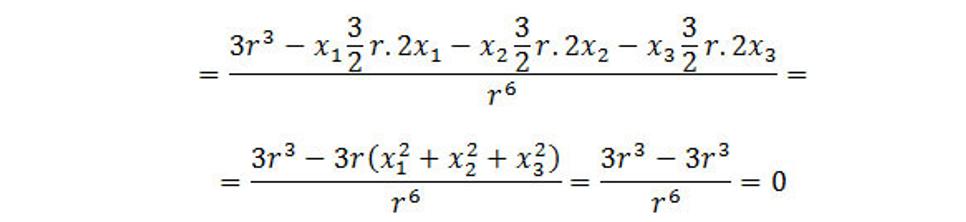
Derivácia podielu je vyjadrená vzťahom:

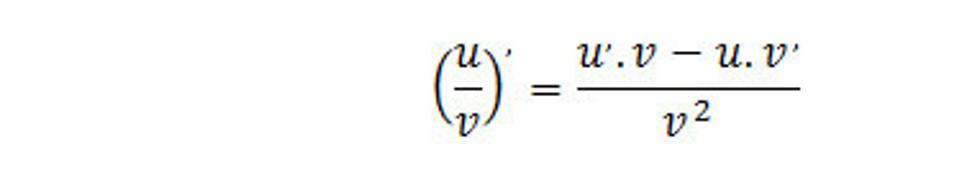
Preto predošlý výraz je v takom tvare ako je.

Alebo platí, že

pre všetky i,

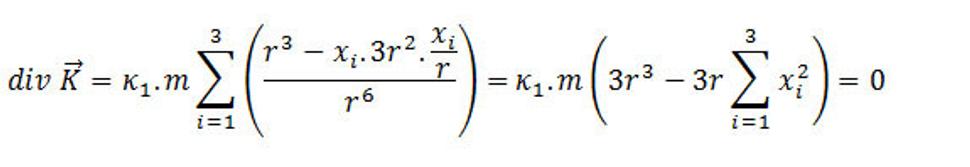
Nech S je uzatvorená plocha v trojrozmernom priestore. Ak S obklopuje hustejší bodový element priestorovej hmoty, tzn. že počiatok súradnicovej sústavy, v ktorej sa nachádza hustejší element priestorovej hmoty leží vo vnútri S, potom tok intenzity K cez S je definovaný nasledovne:

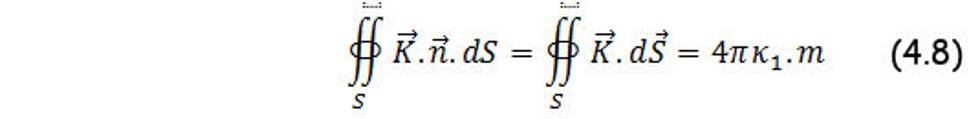
Dokážeme to teraz. Pre zvolenú nejakú guľu |r|≤ε a S viď obr.2 Na základe gaussovej teóremy platí

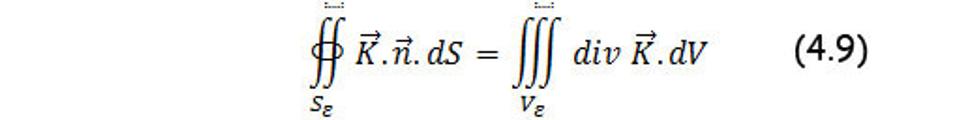
Kde S_ε je uzavretá plocha ohraničujúca V_ε, pravá strana tejto rovnice sa rovná nule, lebo div K =0 v V_ε. Preto

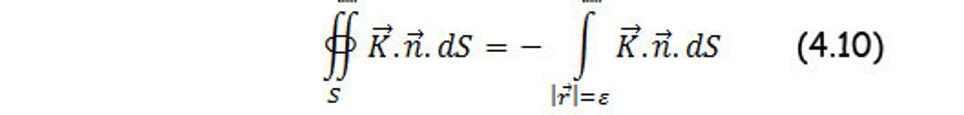
Na guli |r|=ε je

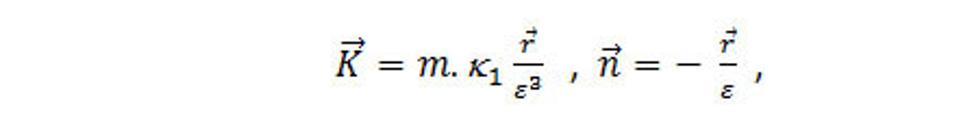
Preto pravá strana tohto vzorca je

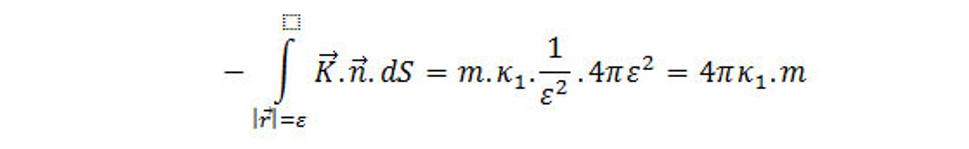
A tak (4.10) dáva výsledok (4.8).

Nech K je intenzita gravitačného poľa, ktorú vytvára konečný počet hmotných elementov ΔV_i lokalizovaných do svojich stredových bodov r₁, r₂, ..., i pre každý i–tý objemový element s väčšou objemovou hustotou poľa ako je v jeho okolí. Ako už vieme, väčšia hustota priestorového poľa v nejakom svojom objemovom elemente vytvára vo svojom okolí gravitačnú silu, alebo okolité body priestorového poľa získavajú na seba vektory gravitačnej sily v radiálnom smere do vnútra hmotného objemového elementu k stredovému bodu, kde tento vektor gravitačnej sily závisí od štvorca vzdialenosti k objemovému elementu a jeho stredovému bodu v ľubovoľnej časti priestorového poľa, kde je väčšia jeho objemová hustota – hustejšie body (kg) ako v jeho okolí.

Nech S je uzatvorená plocha, vo vnútri ktorej sa nachádzajú tieto body. Ak označíme V_ε ako oblasť ohraničenú plochou S a potom aj guľovými plochami |r-r_i|=ε, i=1,2,…,n , tak ďalej, ak zoberieme do úvahy, že div K=0 v V_ε

a Gaussovú vetu, tak dostávame

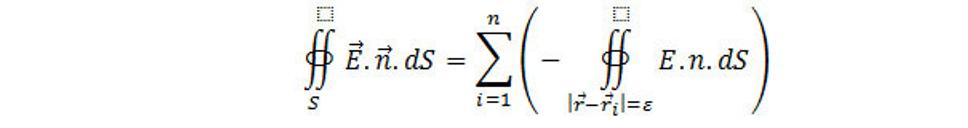
Každý člen v tejto sume, ako bolo uvedené hore, dáva 4πκ ₁ .m

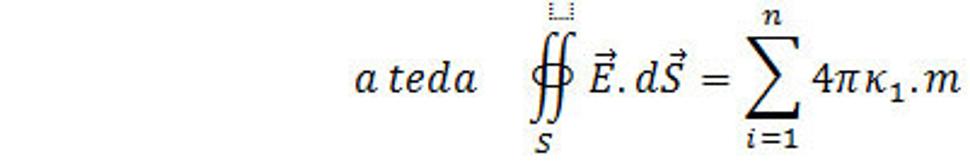
ale

je celková hmotnosť (kg), ktorá je vo vnútri obklopenou S, preto sa dá povedať, že tok intenzity poľa cez uzatvorenú plochu je rovný celkovej hmotnosti obsiahnutej v S násobenej 4πκ₁

toto platí aj pre spojité rozdelenie hmotnosti (kg) v priestore V s hustotou ρ(r)

Nech S je plocha ohraničujúca nejakú časť G z V

Ako predtým, nahradíme hmotnosť vo V pomocou hmotných bodov. Nech r,r,...,i určujú polohu hmotných bodov v G, kde ρ(r_i). ΔV_i je veľkosť hmotnosti v bode r_i a objeme ΔV_i , ktorý predstavuje časť G. Tok intenzity poľa cez S, vytvorenej všetkými hmotnými bodmi vo V je potom

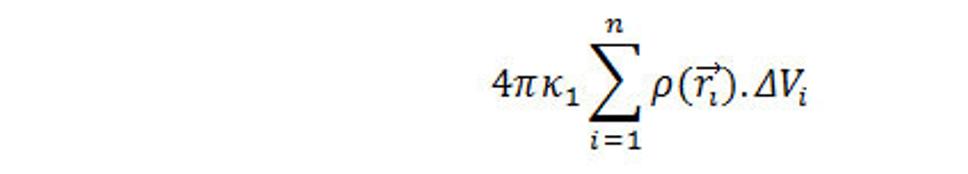
Na základe výsledku (4.7).

dostaneme

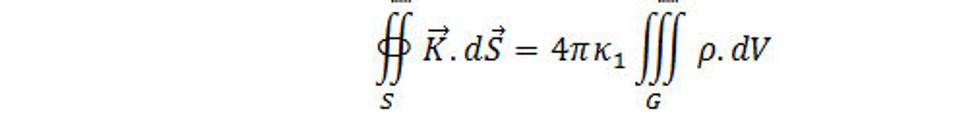
(4.13)

Kde K je intenzita gravitačného poľa vytvorená rozložením hmotných bodov vo G. Ľavú stranu rovnice (4.13) prepíšeme na základe Gaussovej vety, potom dostávame

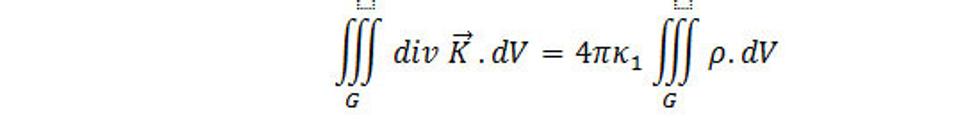
Pretože G je ľubovoľná podoblasť V, potom zo (4.9) vyplýva, že musí platiť

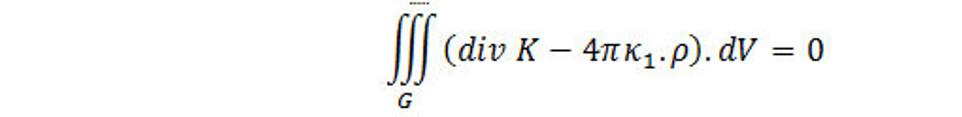
a teda

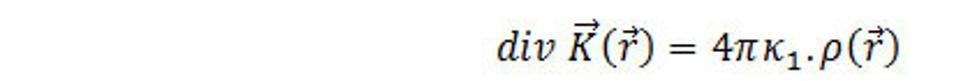
(4.15)

Kontrola fyzikálnych rozmerov v rovnici:

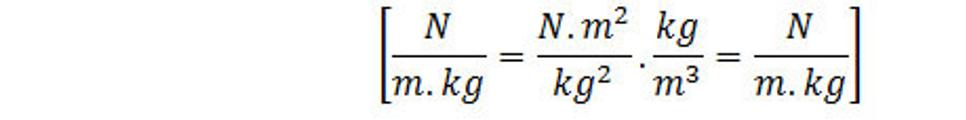
Hustota hmotnosti ρ predstavuje hmotnosť v objemovej jednotke. Výraz div K si môžeme predstaviť ako tok intenzity gravitačného poľa z jednotkového objemu. Rovnica (4.15) predstavuje vzťah medzi intenzitou K a hustotou ρ v tom istom mieste priestoru. Dostali sme ho ako dôsledok vzťahu (4.1), ktorý súvisí s gravitačným zákonom. Platnosť tohto vzťahu je omnoho širší než originálny newtonov gravitačný zákon. Vzťah platí aj tam, kde je prítomná rotácia ba aj v prípadoch, že K a ρ sa menia časom.

Teda

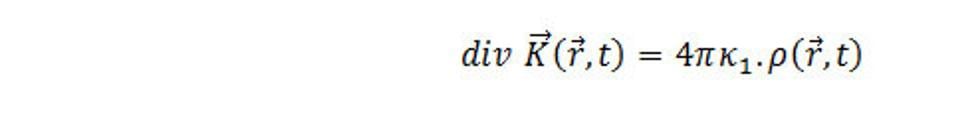
Čo je jedna zo základných rovníc priestorovej interakcie.

Druhá rovnica prvého páru Maxwellových rovníc:

V prípade stacionárneho tečenia priestorovej hmoty, ktorá nezávisí na čase platí nasledovné. Ak položíme nejaký bod M priestorového poľa do počiatku karteziánskej súradnicovej sústavy a umiestnime do tejto sústavy aj rovinu, na ktorej bude tento bod ležať a potom ak sa tento bod priestoru začne pohybovať tak sa začne s ním pohybovať aj rovina a to tak aby bod bol vždy na rovine. Rovina bude sledovať smer pohybu bodu rovnobežne s vektorom svojej normály pričom rovina sa nebude pohybovať voči zvyšným dvom súradnicovým osiam, bude sa len pohybovať jednom plošnom smere. Takto potom bude tento bod na rovine vykresľovať kontúru, ktorá sa nakoniec uzavrie do seba. Prejdenie hmotného bodu M[kg.s^-1], (kde M je množstvo pretečenej hmoty v kg cez plochu S za jednotku času a jej fyzikálny rozmer je M[kg.s^-1]) spolu s rovinou v smere jej normály sa na tejto rovine takto vykreslila do seba uzatvorená kontúra, kde cez plochu ohraničenou touto kontúrou prešiel práve hmotný bod(y), hmotnosť za sekundu M[kg.s^-1], vydelený rotačnou konštantou κ₂[kg²/N.s²] a na bod pôsobí vektor rotačnej interakcie L[1/s], ktorú keď položíme do krivkového integrálu, tak sa dá zapísať aj matematicky

Kontrola fyzikálnych rozmerov v rovnici:

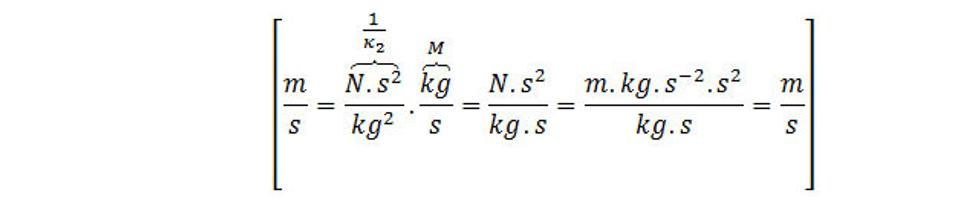
kde

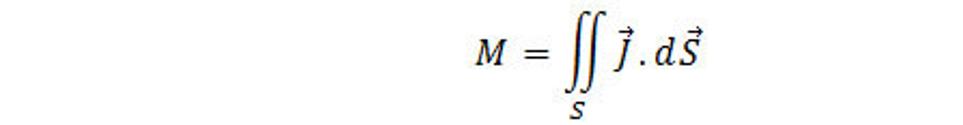
Kontrola fyzikálnych rozmerov v rovnici:

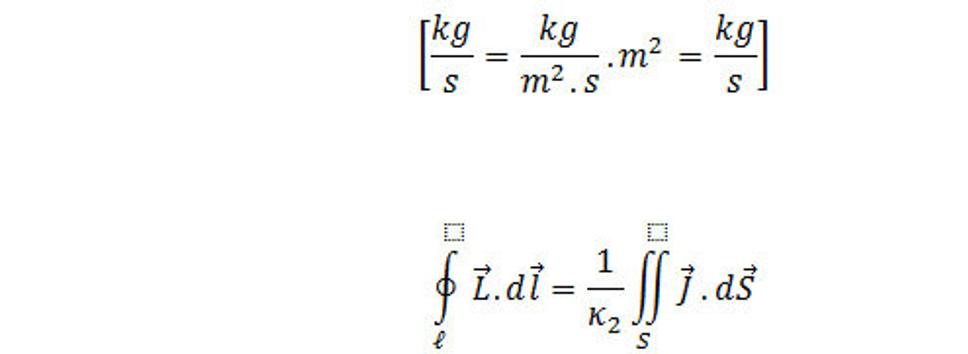
Kontrola fyzikálnych rozmerov v rovnici:

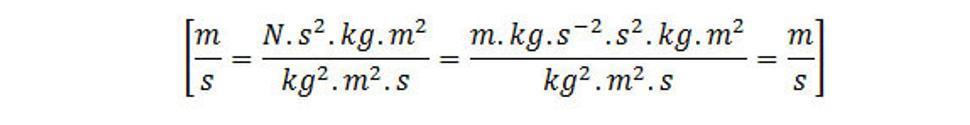
Ľavú stranu rovnice pretransformujeme pomocou Stokesovej teorémy, teda

potom relácia nadobudne tvar

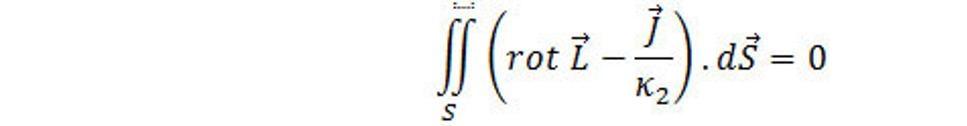
Kontrola fyzikálnych rozmerov v rovnici:

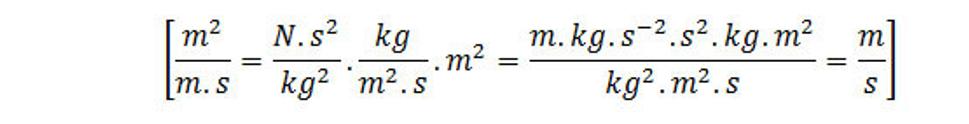
alebo kontrola fyzikálnych rozmerov v rovnici:

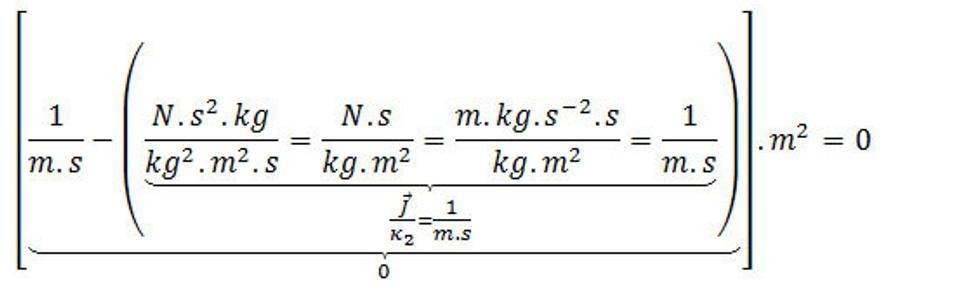
V dôsledku toho, že S je ľubovoľná plocha, preto vyplýva rovnica

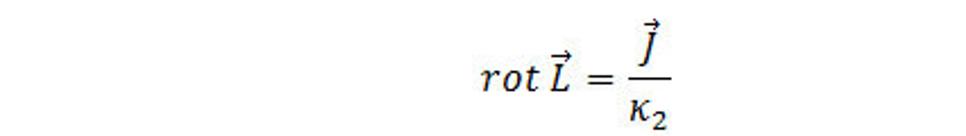
(4.22)

Kontrola fyzikálnych rozmerov v rovnici:

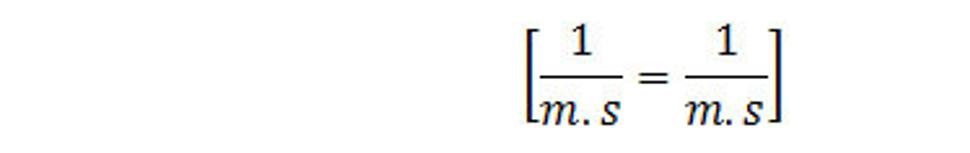
Vidíme, že rotačná interakcia má rotáciu a teda, že má vírivý charakter. Rovnica (4.22) definuje rotáciu rotačnej interakcie v každom bode priestoru v závislosti od hodnoty hustoty toku priestorovej hmoty v tomto bode a platí pre stacionárne tečenie v toku prúdenia, a preto ju nemôžeme považovať za všeobecnú rovnicu priestorovej interakcie. Našim cieľom je nájdenie zovšeobecneného tvaru rovnice (4.22), ktorá bude platiť aj pre nestacionárne prúdenia. K tomu použijeme rovnicu (4.16). Derivujeme ju podľa času. Potom

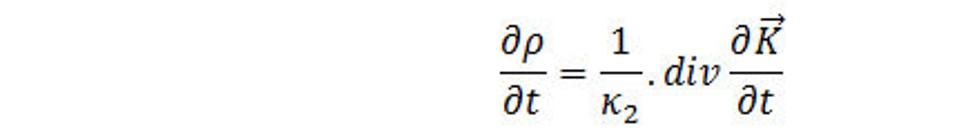
(4.23)

Ak v rovnici kontinuity (2.8) nahradíme časovú deriváciu hustoty priestorovej hmoty pomocou (4.23) dostávame

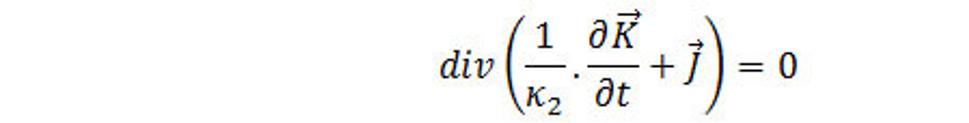
Tento výraz má taký istý tvar, ako rovnica kontinuity pre stacionárne prúdy div J(r) =0

S tým rozdielom, že túto úlohu preberá vektor

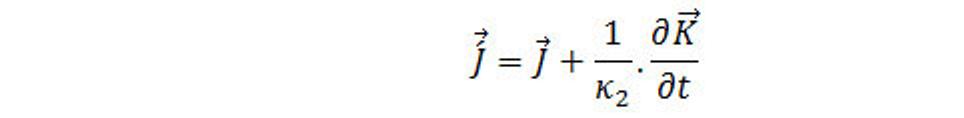
(4.26)

Vektor

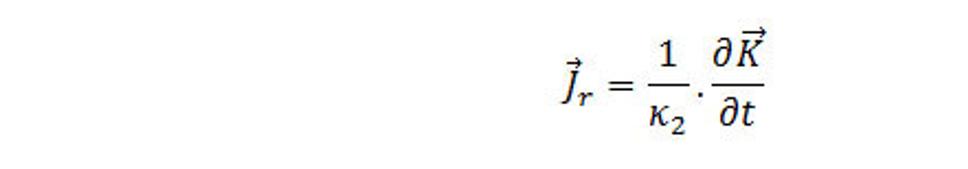
je hustota posuvného toku priestorovej hmoty

Prirodzeným zovšeobecnením (4.19), ktorý je napísaný pre hustotu toku priestorovej hmoty, je použitie tohto vzťahu ak pre prípad, že na pravej strane v integrande spomínanej rovnice vystupuje J_r definovaná vzťahom (4.26). Potom

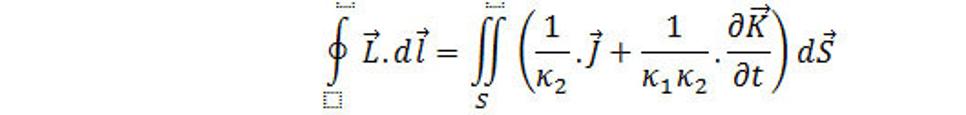
Odkiaľ po aplikovaní Stokesovej vety na ľavú stranu tejto relácie, vyplýva že

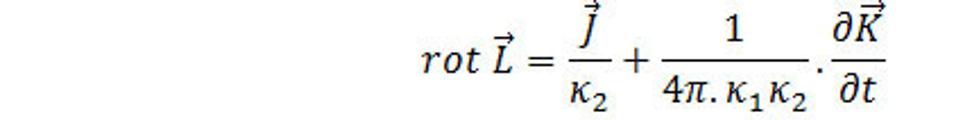
(4.30)

Vzťah (4.30) je ďalšou diferenciálnou maxwellovou rovnicou. Rovnica vyjadruje vzájomnú súvislosť medzi gravitačným poľom a rotáciou tohto poľa. Vidno, že rotácia môže byť vytvorená nielen hustotou priestorovej hmoty, ale tiež aj zmenou gravitačného poľa. V tomto paragrafe sme odvodili dve základné rovnice, ktoré obsahujú zdroje (hustotu toku priestorovej hmoty a hustotu priestorovej hmoty). Rovnice (4.16) a (4.30) sa nazývajú prvým párom Maxwellových rovníc.

5.Druhý pár Maxwellových rovníc.

Pri zavedení pojmu rotácie ako jednej z interakcií priestorového poľa je jasné, že voľné rotácie sa v prírode nevyskytujú. Rotácia sa vždy viaže s nejakým bodom, ktorý rotuje alebo s druhou interakciou - gravitáciou a tieto dve interakcie vytvárajú hmotný bod priestoru a teda rotácia sa samostatne nevyskytuje, aby nebola viazaná na hmotný bod. Dá sa to chápať aj inak. Priestorové pole je dvojzložkové pole so vzájomne previazanými interakciami, ktoré sú na seba kolmé. Ľubovoľný bod priestoru sa dá vyjadriť komplexným číslom, kde reálna zložka bude gravitácia a imaginárna zložka rotácia. Ak imaginárnu zložku dáme do nasledujúcich vzorcov tak výsledok bude vždy nula, lebo imaginárna zložka bez reálnej zložky nedá reálny výsledok a teda výsledkom bude vždy nula na reálnej číselnej osi. Preto ak si zavedenie fyzikálnu veličinu – tok rotácie, tak tento tok cez uzatvorenú plochu S s jednotkovou normálou n sa bude rovnať nule. A bude platiť

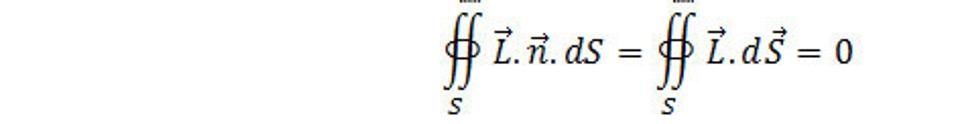
(5.1)

Tento výsledok nezávisí ani na veľkosti, ani na tvare plochy a tiež nie na zmene L s polohou a časom. Zároveň (5.1) zostáva v platnosti nezávislé na spôsobe akým je rotácia produkovaná. Platnosť vzťahu (5.1) nie je porušená ani prítomnosťou gravitačného poľa. To znamená, že rovnica (5.1) vyjadruje všeobecný zákon priestorovej interakcie. Pomocou Gaussovej vety pretransformujeme ľavú stranu v (5.1) a dostávame

(5.2)

Táto rovnosť platí pre ľubovoľný objem (plocha S ohraničujúca V je ľubovoľná), a preto z (5.2) vyplýva, že

(5.3)

Ďalšou Maxwellovou rovnicou je

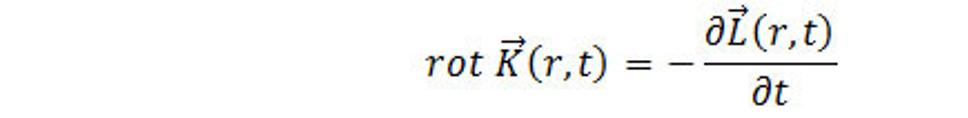
(5.9)

Odvodenie vzťahu ako poslednej maxwelllovej rovnice z hľadiska priestorovej interakcie je rozsiahle a najťažšie, a teraz ho nebudem uvádzať, lebo je to extrémne náročné na opis z dôvodov veľkého úsilia na predstavivosť. Ponechám si ho zatiaľ pre seba.

Napíšme si teraz sústavu Maxwellových rovníc priestorového poľa vo vákuu.

I. Pár:

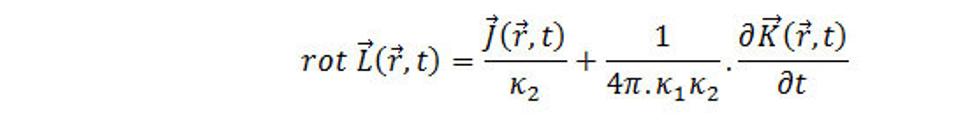
(6.1)

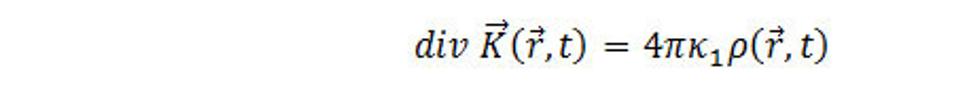
(6.2)

II. Pár:

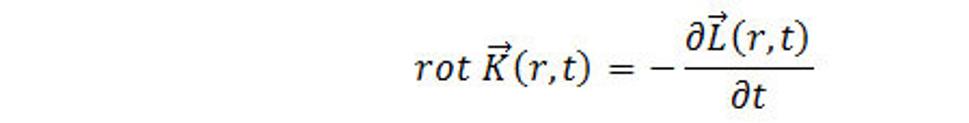
(6.3)

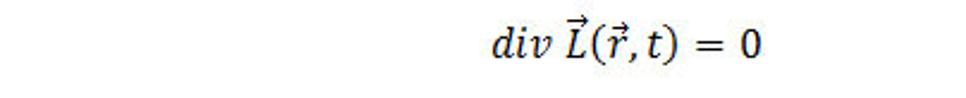
(6.4)

V týchto rovniciach považujeme ρ a J za známe. Neznáme sú komponenty vektorov gravitačného poľa K a rotácie L. Máme teda šesť neznámych a osem rovníc pre ne.

6.Vektorový a skalárny potenciál

Maxwellové rovnica predstavujú sústavu navzájom zviazaných parciálnych diferenciálnych rovníc, ktoré určujú zmeny gravitačnej a rotačnej interakcie. Pre jednoduché prípady možno ich riešiť bezprostredne. Je ale výhodné zaviesť potenciály a prepísať takýto systém na menší počet rovníc druhého rádu. Pritom dve Maxwellové rovnice sú splnené automaticky. Pretože div L=0

Je postačujúce vyjadriť L pomocou rovnice

(9.1)

Kde A(r,t) je vektor, ktorý sa nazýva vektorový potenciál, kde r v zátvorke je polohový vektor. Ak dosadíme (9.1) do rovnice (7.3), dostaneme

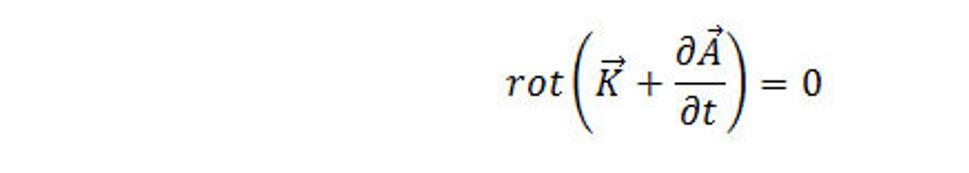
(9.2)

Veličina v okrúhlych zátvorkách, ktorej diferenciálna charakteristika – rot sa rovná nule, možno vyjadriť v tvare gradienta nejakej skalárnej funkcie – skalárneho potenciálu φ(r,t) kde r v zátvorke je polohový vektor. Teda

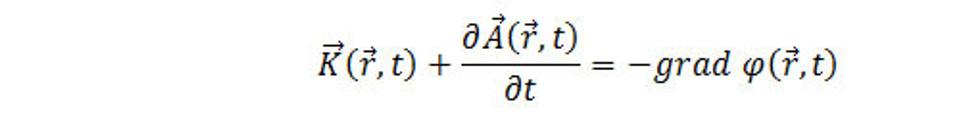
alebo

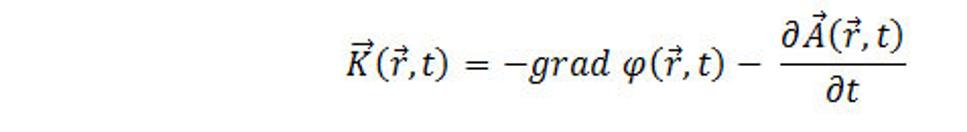
(9.3)

Interakcie sú určené pomocou potenciálov priestorovej interakcie A a φ vzťahmi (9.1) a (9.3) identicky spĺňajú Maxwellové rovnice (7.3) a (7.4). Dynamické správanie sa A a φ je definované zostávajúcimi rovnicami (7.1) a (7.2).Ak dosadíme (9.3) do rovnice (6.2), dostaneme

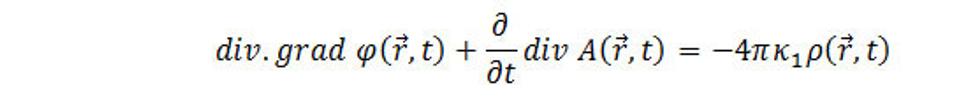
alebo

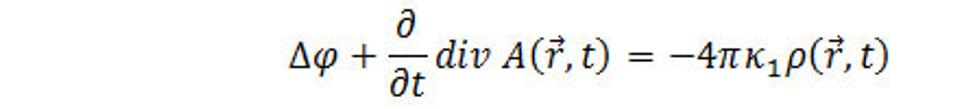
(9.5)

Podobne ak dosadíme za vektory K a L výrazy (9.3) a (9.1) do Maxwellovej rovnice (6.1), dostaneme po úprave

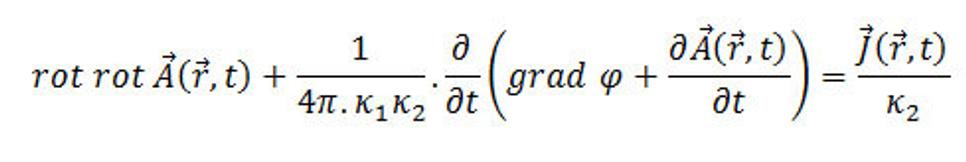
(9.6)

Ak použijeme vektorovú totožnosť

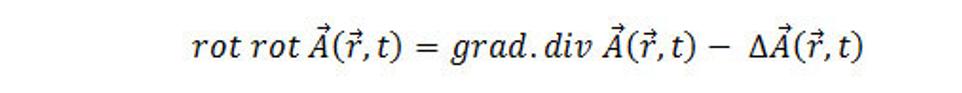
(9.7)

rovnica (9.6) nadobudne tvar

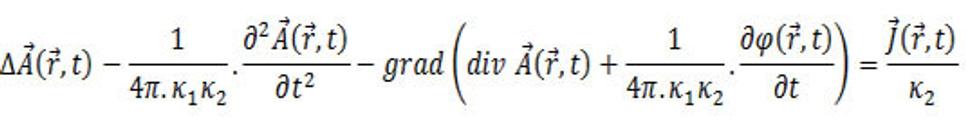
(9.8)

Takýmto spôsobom sme previedli sústavu štyroch Maxwellových rovníc na sústavu dvoch rovníc, ktoré jednako zostali vzájomne prepojené. K tomu, aby sme získali rovnice jednotlivo pre φ a A, využijeme voľnosť definícii potenciálov priestorového poľa, pretože rotácia L súvisí s A, ktorý je daný vzťahom (9.1), je zrejmé, že vektorový potenciál je určený s presnosťou až na aditívnu vektorovú funkciu, ktorá je gradientom ľubovoľnej funkcie Ψ(r,t). rotácia sa nemení pri transformácii

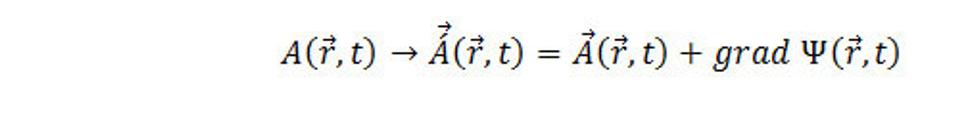
(9.9)

Skutočne

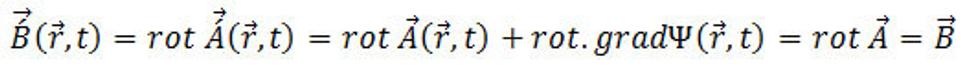
(9.10)

Využila sa známa vektorová identita rot.grad Ψ = 0. Aby pri takejto zámene nenastala ani zmena gravitačného poľa, ktoré je určené reláciou (9.3), treba urobiť súčasne aj transformáciu skalárneho potenciálu. Dosaďme do rovnice (9.3) za vektor A zo vzťahu (9.9), potom

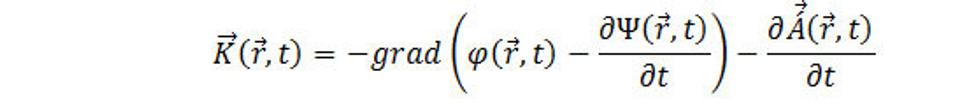
(9.11)

Ak urobíme zámenu

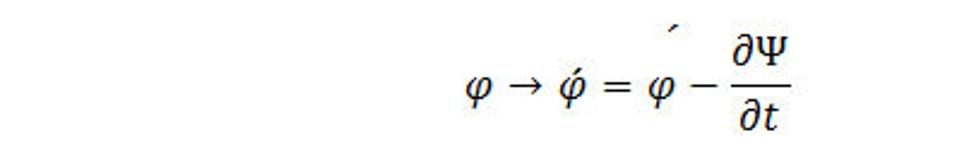
Dostaneme pre intenzitu K výraz, ktorý je zhodný s (9.3). Dá sa povedať, že skalárny potenciál je určný s presnosťou derivácie času funkcie Ψ. Vzťahy (9.9) a (9.12) umožňujú vybrať takú dvojicu potenciálov, ktoré vyhovujú podmienke

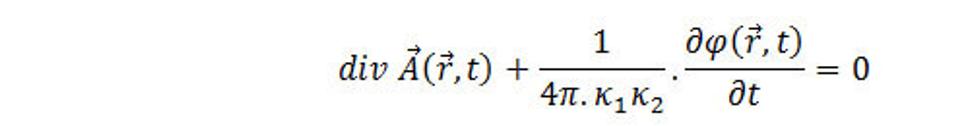
V takomto prípade rovnice (9.5) a (9.8) prejdu na dve nehomogénne parciálne diferencálne rovnice druhého rádu φ a vektor A

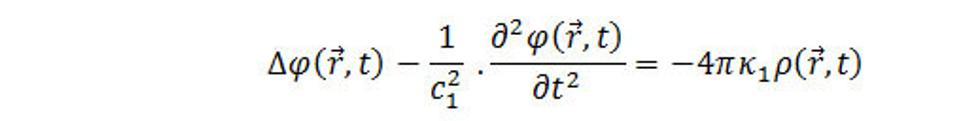
(9.14)

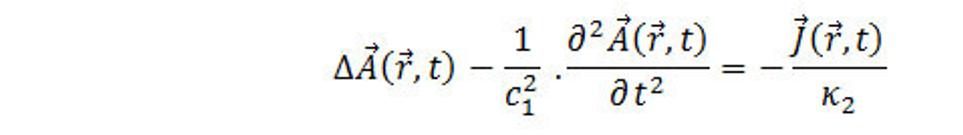
(9.15)

Položili sme

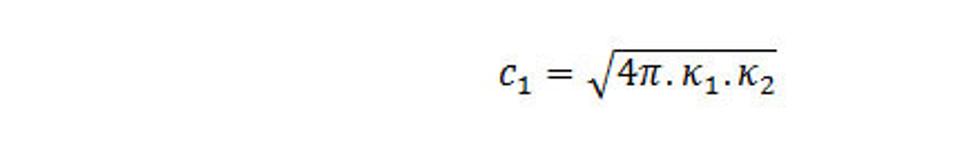
Kde c1 je rýchlosť priestorových vĺn (priestorónov) vo vákuu. Nájdené rovnice pre priestorové potenciály sú ekvivalentné pôvodným Maxwellovým rovniciam.

Vidíme, že priestorové pole je v opise formálne totožné s EM poľom, menia sa len rozmery fyzikálnych veličín a konštanty, čím sa stáva toto pole niečím úplne iným ako EM pole. Preto je logické, že opis tohto poľa sa prispôsobí konštantám a pre priestorové pole potom bude platiť prevrátená alebo podobná logika aká je v teórii relativity, budú tu len iné rozmery fyzikálnych veličín a konštanty vo vzorcoch pri tomto inom relativistickom opise. Už som uviedol konštantu c1. Ide o inú, ale podobnú konštantu aká je v teórii relativity, ide o tzv. najpomalšiu rýchlosť, ohraničenie pre rýchlosť zdola. Potom je zrejmé, ak uvážime, že priestorové pole preberá určitú logiku z teórie relativity, že bude platiť výraz pre priestorónovú energiu

Kde Q je elektrický náboj – čo je fyzikálny rozmer pre elektromagnetickú hmotu, c1 je najpomalšia rýchlosť, E_p je priestorónová energia a jej rozmer je [C.m^2.s^(-2) ] a skutočne. Známa Einsteinova rovnica je

Kde E_f je fotonová energia a jej rozmer je [kg.m^2.s^(-2) ]

Rozmer EM hmoty je Coulomb C a rozmer priestorovej hmoty je Kilogram Kg. Vidíme, že ide o výmenu fyzikálnych rozmerov vo vzorcoch, kde fotónová energia sa vypočíta z kilogramov krát štvorec najrýchlejšej rýchlosti a priestorónová energia sa vypočítava z coulombov krát štvorec najpomalšej rýchlosti. Toto nie je náhoda a je to fyzikálne dôležitá skutočnosť. Takže celý ten povyk, ktorý tu bol urobený z mojej strany okolo matematického opisu priestoru bol preto, aby som poukázal na uvedené vzťahy energie. Na základe tohto vzťahu energie odvodíme všetky konštanty pre opis priestorového poľa.

Zhrnutie výsledkov:


. Z teologického hľadiska ide o Boha (priestorové pole) a Satana (EM pole) a sú voči sebe ako protiklady aj keď z hľadiska opisného formálne totožné ale z hľadiska podstaty sú to protiklady. Boha je v celom kozme viacej a Satana je menej, teda Boh prevláda asi 8:1.

Zákon zachovania energie.

Majme sústavu hmotných bodov priestorovej hmoty mi (i=1,2,...,n), ktoré sa pohybujú rýchlosťou vektor vi. Pohybová rovnica pre i-tý hmotný bod priestorovej hmoty sa dá napísať v nasledovnom tvare:

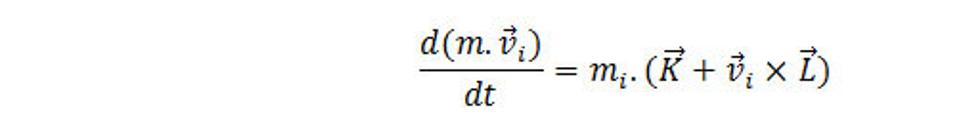
Kde m.v_i [kg.m.s-1] je hybnosť bodu priestorovej hmoty v sústave bodov priestorovej hmoty, kde energia sústavy sa čerpá z fyzikálneho rozmeru energie, ktorý je vo fyzikálnom tvare [kg.m².s^-2]. Derivácia hybnosti m.v_i [kg.m.s^-1] podľa času bude [kg.m.s^-2], čo je N,

Ak vynásobíme rovnicu skalárne vektorom vi dostaneme:

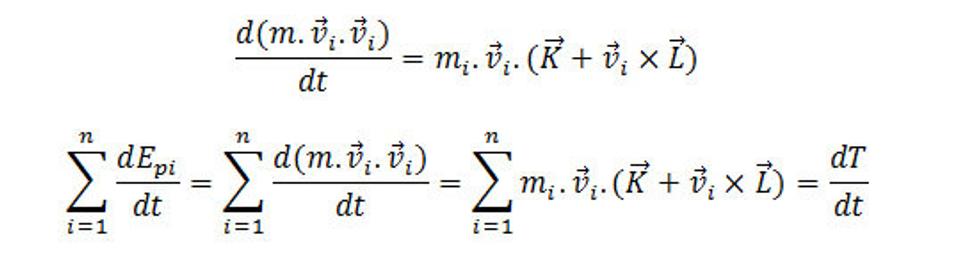
Pri skalárnom vynásobení výrazu rýchlosťou v _i bude tento výraz rovný nule, lebo rotácia nekoná prácu, keďže táto rotácia je kolmá na túto rýchlosť v a takýto súčin dvoch vektorových síl je rovný nule, lebo cos 90 =0 a v.L=0, lebo skalárny súčin dvoch vektorov sa vyjadruje v . L=v.L.cos(v,L), kde v je kolmé na L čo je 90 a teda sa rovná nule.

Práca, ktorú vykoná priestorová interakcia (pole) na sústave hmotných bodov priestorovej hmoty za jednotku času (výkon) je vyjadrená vzťahom

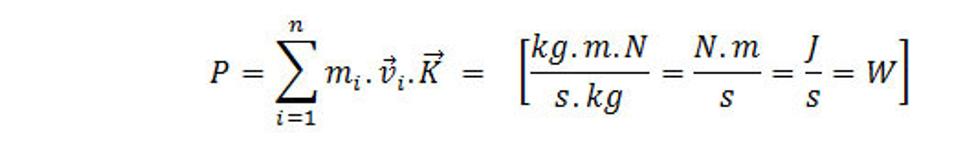
Pre spojité rozloženie hmoty a teda aj bodov priestorovej hmoty v objeme V, môžeme využiť hustotu hmoty ρ=m/V a hustotu toku priestorovej hmoty J=ρ.v. Potom celkový výkon priestorovej interakcie (poľa) v objeme V je určený vzťahom

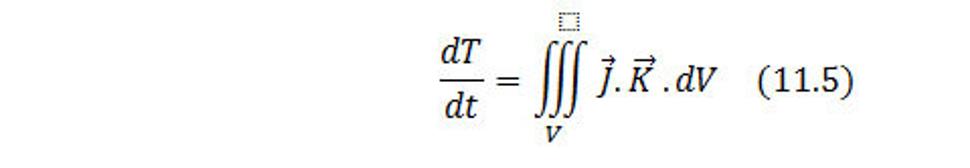
Z rovnice

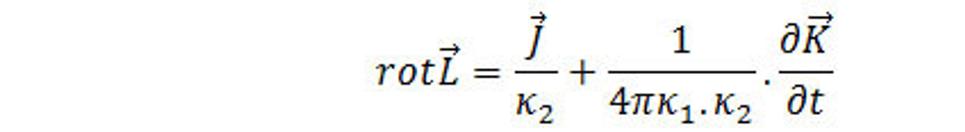
Vyplýva, že

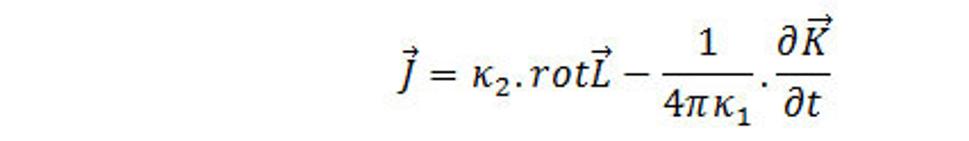
Ak to použijeme, dá sa rovnica

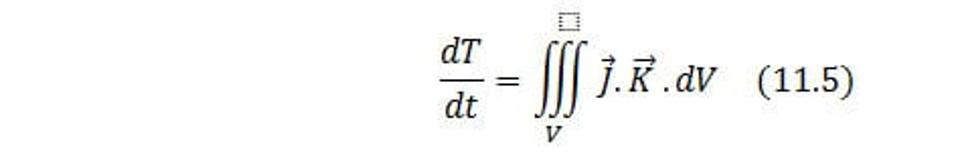
Napísať v tvare

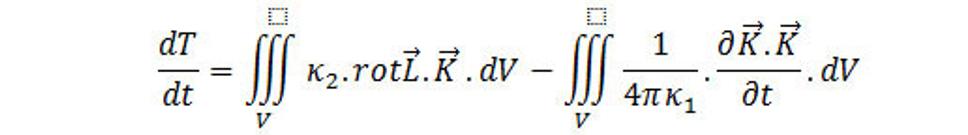
S ohľadom na vektorovú reláciu, že

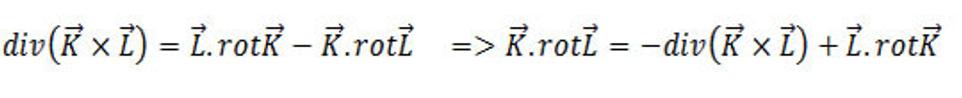
A že

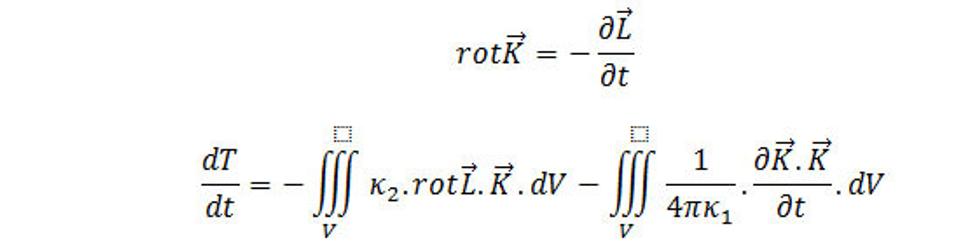
Za rot L . K dosadíme - div( K × L) – L .∂ L /∂t, kde za rot K sme vo výraze - div( K × L) + L .rot K dosadili rot K =-∂L/∂t.

a teda

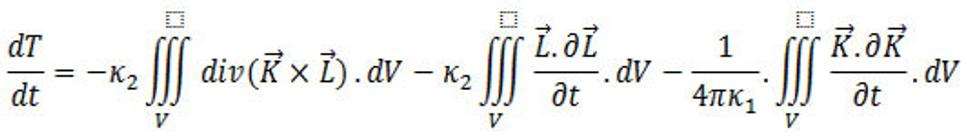
Pravú stranu tejto rovnice s prihliadnutím na Gaussovú vetu je možné upraviť. Pokračovanie úpravy tejto rovnice nájdete v druhej časti tohto blogu, lebo rovnice odovzdané do tohto blogu ako fotky sa už nezmestia do prílohy - súborový manažér a nie je ďalej možné písať tento blog s ďalšími fotkami - vzorce, aby to bolo všetko v jednom blogu. Preto reagovať príspevkami na tento blog bude možné až v jeho druhej časti, kde jeho pokračovanie je - tu -