Intuitívna predstava toho, čo je rovné a čo je krivé, je jasná. Pozrime sa napr. na obrázok 1, kde figuruje niekoľko geometrických útvarov, tj. priamka, kružnica a dve (čierne) úsečky. Intuitívne priamku i úsečky považujeme za rovné, kým kružnica je príkladom tzv. krivky, je teda už podľa mena krivá. Tejto intuitívnej krivosti sa v matematike i fyzike hovorí vonkajšia krivosť, ale krivosť, o ktorú ide v Einsteinovej teórii gravitácii, nie je táto vonkajšia, ale je menej intuitívna; hovorí sa jej vnútorná krivosť. Ukazuje sa napr., že kružnica na obrázku 1 má nulovú vnútornú krivosť a teda je vnútorne rovná, alebo, ako sa tiež hovorí, je vnútorne plochá.
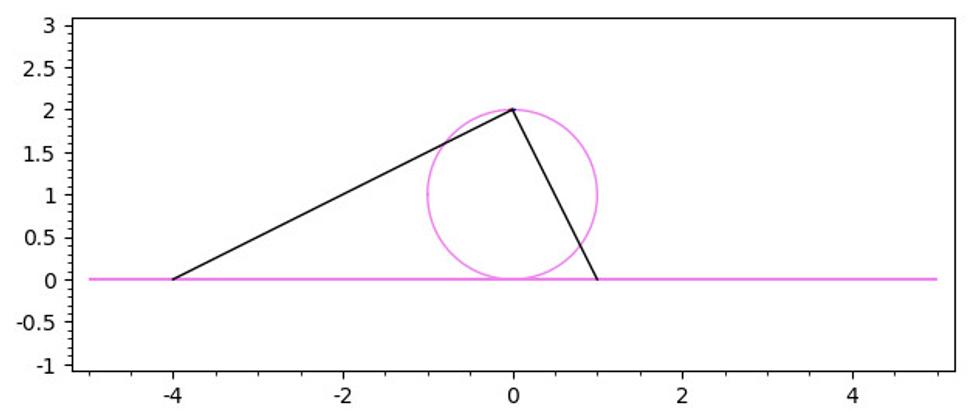
Definovať matematicky pojem vnútornej krivosti presahuje rámec tohoto blogu, jednako sa pokúsim ho čitateľovi aspoň trochu priblížiť na niekoľkých príkladoch. V prvom rade však zdôrazním, že je to vlastnosť lokálna a teda vždy hovoríme o krivosti v okolí nejakého bodu. Predstavme si napr., že ľavá úsečka na Obr. 1 je natiahnutá čierna niť, ktorá sa dá deformovať ohýbaním, ale nedá sa deformovať naťahovaním. Túto niť môžeme ľahko zavinúť do kružnice a tým zmeniť VONKAJŠIU geometriu nite ako objektu uloženého v rovine, ale toto zavinutie nezmení VNÚTORNŮ geometriu nite v okolí nejakého jej bodu (okrem bodov koncových, ktoré musia byť študované osobitne). V dotyčnom okolí dva body nite vzdialené od seba pred zavinutím jeden centimeter, zostanu od seba vzdialené jeden centimeter aj po zavinutí. Vnútorná krivosť je čisto lokálnou charakteristikou tejto vnútornej geometrie, nemalo by teda prekvapovať, že je tá istá (konkrétne nulová) aj pre rovnú niť aj pre zavinutú, mimimálne teda v nekoncových bodoch nite. Koncové body nite splynú v jeden bod na kružnici, čo je prípad, ktorý sa musí ošetriť osobitne, ale nakoniec sa to dá urobiť tak, aby aj tam bola vnútorná krivosť nulová.
Pozrime sa, ako vyzerajú veci o rozmer vyššie, Za týmto účelom nahradíme Obr. 1 jeho vyššie rozmerným analógom obrázkom 2.
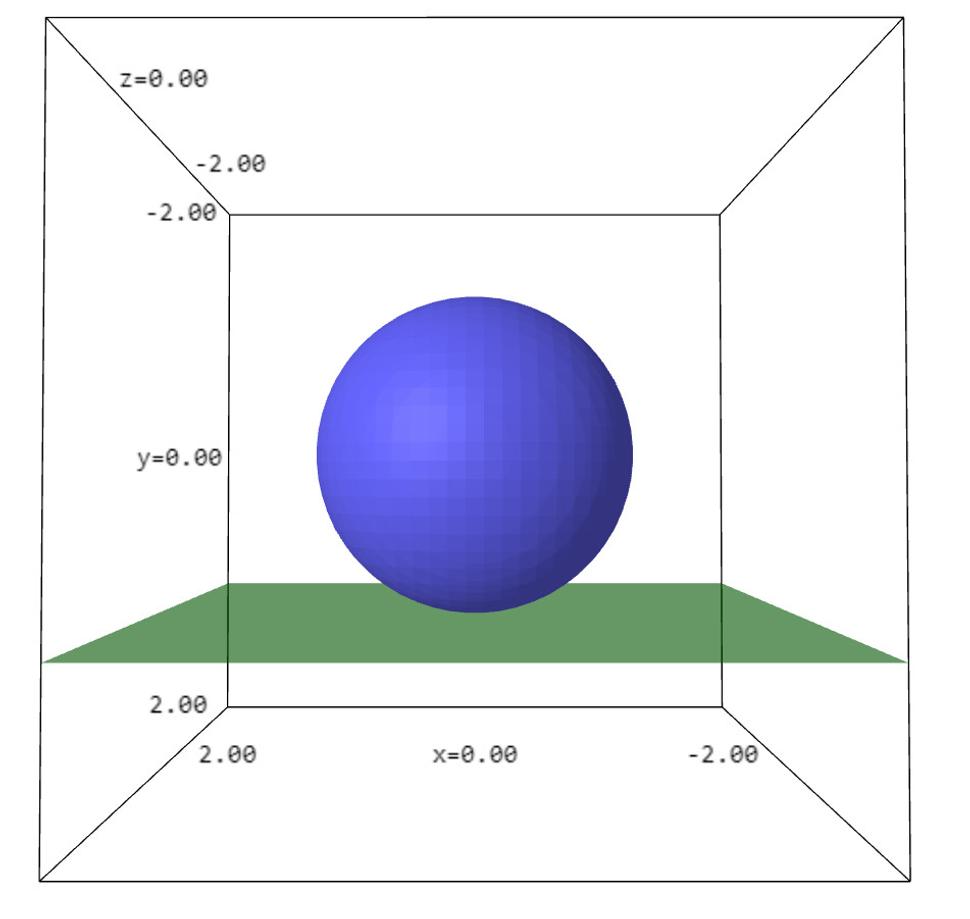
Ukazuje sa, že v tomto prípade je povrch gule krivý nielen navonok, ale i vnútorným spôsobom. Ako príklad uvažujme štandardnú okrúhlu geometriu na našej zemeguli (podľa ktorej určujú aerolínie najkratšie trajektórie lietadiel). Ukazuje sa, že táto geometria je vnútorne krivá. Je pozoruhodné, že bez toho, aby sme presne matematicky rozumeli pojmu vnútornej krivosti, môžeme s pomocou jednoduchého uhlomeru určiť nielen to, či je nulová alebo nenulová, ale aj spoznať jej znamienko. Ak si zvolíme na zemeguli tri mestá ako napr. Bratislavu, Marseille a Bukurešť a nakreslíme najkratšie cesty, ktoré ich spájajú (trasy lietadiel), dostaneme útvar zvaný sférický trojuholník (viď Obr. 3).

Na rozdiel od štandardnej rovnej geometrie roviny, kde je súčet uhlov ľubovoľného trojuholníka rovný 180 stupňom, súčet uhlov sférického trojuholníka presahuje 180 stupňov. Toto je známkou KLADNEJ vnútornej krivosti povrchu gule. Poznamenajme tiež, že existujú aj dvojrozmerné povrchy, ktoré majú negatívnu vnútornú krivosť. Hovorí sa im hyperbolické a súčet uhlov v trojuholníku je v nich menší ako 180 stupňov.
Poďme teraz ešte o rozmer vyššie, konkrétne by sme chceli vedieť, či je trojrozmerný priestor, v ktorom žijeme, krivý alebo nie. Túto otázku si ako prvý položil nemecký matematik Gauss, ktorý pojem vnútornej krivosti vymyslel. Bolo to ešte v devätnástom storočí, pred Einsteinom, keď ešte nikto nepodozrieval, žeby niekto mal nazerať na náš trojrozmerný priestor ako na niečo vnorené do štvorrozmerného priestoročasu alebo žeby geometria mala mať niečo spoločného s gravitáciou. Keďže teda Gauss náš trojrozmerný priestor neuvažoval ako súčasť niečoho vyššie rozmerného, snažil sa zistiť iba to, či má VNÚTORNÚ krivosť. Urobil to meraním uhlov. Vyškriabal sa na vysoký alpský končiar A, vybral si na horizonte iné končiare B a C a zmeral uhol medzi nimi (celý horizont má samozrejme 360 stupňov). Potom sa vyškriabal na končiare B a C a keď všetky tie tri zmerané uhly sčítal, vyšlo mu 180 stupňov. Usúdil teda, že náš skutočný priestor nie je zakrivený.
Keby sme dnes zopakovali Gaussov alpský experiment s presnejšími uhlomermi, nevyšlo by nám 180 stupňov, pretože naša Zem zakrivuje svojou hmotou priestor (aj priestoročas) okolo seba. Nuž a teraz si môžeme uvedomiť silu Einsteinovho génia, ktorý to predvídal. Keď Einsteina napadla myšlienka, že gravitácia je geometria, nenechal sa odradiť výsledkom Gaussovho experimentu. Veril tomu, že ak by mal Gauss presnejšie prístroje, nejakú maličkú odchýlku od 180 stupňov by nameral. Pritom menej nadaný človek ako Einstein by si povedal, že ak je gravitácia Zeme taká silná, že pri páde z výšky sa ľahko môžeme zabiť, azda by sa dalo očakávať, že to zakrivenie priestoru okolo Zeme by malo byť dosť markantné na to, aby ho Gauss svojím experimentom odhalil. Jednako Einstein pevne veril v krásu matematických princípov, na ktorých založil svoju teóriu, a dopracoval ju do konca, nenechajúc sa odradiť výsledkom Gaussovho experimentu.
Ako som už spomínal v minulom blogu, teória gravitácie je v prvom rade geometriou štvorrozmerného priestoročasu a iba odvodene geometriou trojrozmerného priestoru. Ten priestoročasový geometrický pohľad je pritom laikovi isto vzdialenejší ako ten čisto priestorový. Vskutku, zatiaľčo každý človek dobre chápe pojem uhlu medzi dvoma priestorovými smermi, ktorého laika by napadlo, že uhol medzi jedným priestorovým a jedným časovým smerom má niečo do činenia s pojmom rýchlosti? A predsa je to tak. A tak možno neprekvapí, že na určenie, či je nejaký štvorrozmerný priestoročas krivý, nemusíme nutne používať uhlomer ako Gauss, ale môžeme použiť trebárs i zrkadlo a hodiny. Preilustrujem to na tejto historke:
Istý fotón sa oženil s alfa časticou a v manželstve im to vcelku klapalo. Kým fotón holdoval ako koníčku behu na dlhé vzdialenosti, jeho polovička zasa rada čítala horory o rozpade alfa častíc. Keď si chcela niečo v kľude prečítať, vyslala svojho manžela trebárs na planétu Mars, ktorý sa tam odrazil od zrkadla a zhruba po hodine doletel nazad domov. Jednako občas sa stávalo, že manžel priletel domov skôr, než manželka napínavý horor dočítala. Raz preto alfa častica zatelefonovala svojmu priateľovi teoretickému fyzikovi a povedala mu, že číta zhruba jednu stranu za minútu, že jej nový horor na prečítanie má päťsto strán a či by jej teda neporadil, ku ktorej planéte má manžela vyslať, aby sa nevrátil priskoro. Nuž a teoretický fyzik by jej odpovedal jedným z troch možných spôsobov, v závislosti od toho, či má náš vesmír ako priestoročas kladnú, nulovú alebo zápornú krivosť.
Odpoveď fyzika v prípade kladnej krivosti:
Neboj sa, drahá priateľka, je vo vesmíre plno takých miest, kam môže tvoj manžel poletieť a vrátiť sa domov až potom, keď budeš mať tvoj päťstostranový horor prečítaný. Dávaj len pozor, aby si zle nevybral cieľ svojho výletu, pretože sú aj také miesta, odkiaľ sa ti manžel nedokáže vrátiť, hoci letí rýchlosťou svetla.
Odpoveď fyzika v prípade nulovej krivosti:
Neboj sa, drahá priateľka, nájdem ti také miesta. Ba aj v budúcnosti, hoci by mal tvoj nový horor bárs aj tisíc či milión strán, nájdem ti zodpovedajúce miesta.
(Všimnime si, že tu už fyzik alfa časticu nevaruje, že jej manžel sa môže z cesty aj nevrátiť, pretože vo vesmíre s nulovou krivosťou niet takého rizika.)
Odpoveď fyzika v prípade zápornej krivosti:
Nuž nepoteším ťa, drahá priateľka. Náš vesmír je síce priestorovo nekonečný, má ale zápornú krivosť a keď aktuálne zoberiem do úvahy veľkosť tej krivosti, vychádza mi to tak, že kamkoľvek by tvoj manžel neletel, vráti sa ti, kým stihneš prečítať nanajvýš štyristo dvadsaťdva strán. Na päťstostranové horory teda radšej zabudni.
Nuž a pozoruhodné na tom je, že ten fotón letí vo všetkých troch prípadoch rýchlosťou svetla. Zaujímavé, že?






