Na predchádzajúcich blogov som sa snažil objasniť pojmy kategórie, vyššej kategórie a tiež funktoru ako zachovávajúceho zobrazenia medzi (vyššími) kategóriami. To všetko teraz použijem na objasnenie toho, čo je to topologická kvantová teória poľa v jednej dimenzii, alebo, inak povedané, topologická kvantová mechanika. Zdôrazňujem, že topologická kvantová mechanika nemá nejaké zvlášť hlboké matematické či fyzikálne aplikácie, ale nám poslúži ako výborný ilustračný model ideí, ktoré budú hrať úlohu v podstatne bohatšej topologickej kvantovej teórii poľa vo vyšších dimenziách.
Základná definícia:Topologická kvantová mechanika je 2-funktor medzi geometrickou 2-kategóriou “otvorených orientovaných vrstevníc” OOV a algebraickou 2-kategóriou matíc Mat.
Naším najbližším cieľom bude najprv podrobne preskúmať štruktúru 2-kategórií OOV i Mat a až v nasledujúcom blogu zostrojíme príklad príslušného 2-funktora. Začneme od popisu cieľovej algebraickej 2-kategórie Mat, o ktorej už z blogu “O monoidoch a kategóriách” (https://ctiradklimcik.blog.sme.sk/c/459003/o-monoidoch-a-kategoriach.html) vieme, že je to 1-kategória, ale ešte nevieme, že sa dá taktiež vybaviť štruktúrou 2-kategórie. Ujasnime si teda najprv tento fakt.
Prvkami 2-kategórie Mat sú reálne matice, čiže obĺžnikové schémy s istým počtom riadkov a istým počtom stĺpcov; na priesečníku každého riadku a stĺpca sedí jedno reálne číslo. Tu sú príklady takýchto matíc:
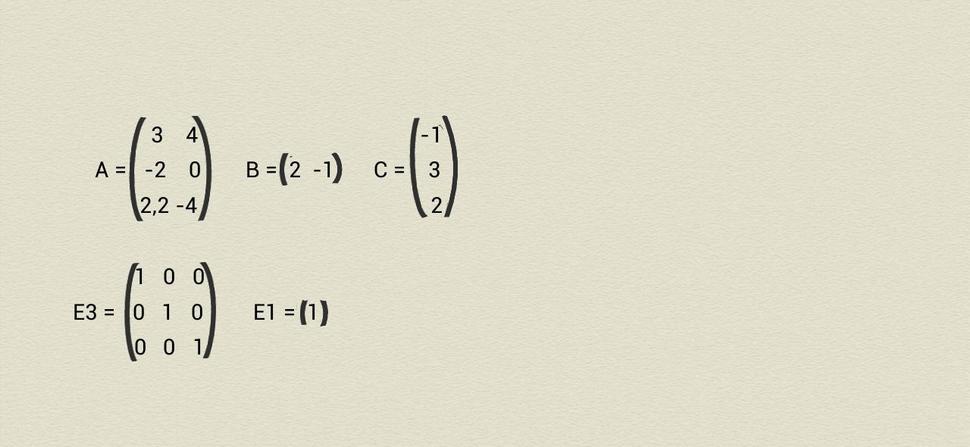
Základnými charakteristikami matice sú počty jej riadkov a stĺpcov. Napr. matica A má tri riadky a dva stĺpce a napr. na priesečníku tretieho riadka a prvého stĺpca sa nachádza číslo 2,2. Matica B má jeden riadok a dva stĺpce a ako každá matica s jedným riadkom sa nazýva lineárna forma. Matice s jediným stĺpcom ako napr. matica C sa nazývajú vektory.
Každá 2-kategória musí mat svoje 1-jedničky a 2-jedničky: V 2-kategórii Mat je jediná 1-jednička E1, má jeden riadok a jeden stĺpec a na ich priesečníku je číslo 1 (viď Obr.1). 2-jedničiek je v 2-kategórii Mat samozrejme viac a sú to všetky matice s rovnakým počtom riadkov ako stĺpcov, ktoré majú všade na diagonále číslo 1 a všade mimo diagonály číslo 0 (viď Obr.1, kde je explicitne uvedená 2-jednička E3).
V zmysle môjho blogu “O vyšších kategóriách” (https://ctiradklimcik.blog.sme.sk/c/463075/o-vyssich-kategoriach.html) nám do plného popisu 2-kategórie Mat ešte zostáva zadefinovať súčiny. Začnime od 1-súčinu, ktorý sa často nazýva direktným súčinom matíc a je definovaný pre ľubovoľné dve matice (je to teda úplný a nielen čiastočný súčin, čo je v zhode s existenciou jedinej 1-jedničky E1). Direktný súčin matice A s m riadkami a n stĺpcami a matice B s k riadkami a l stĺpcami je matica A@B s m×k riadkami a n×l stĺpcami, ktorá sa získa prenásobením každého prvku matice A s celou maticou B. Ako príklad uveďme direktný súčin matíc z predchádzajúcich príkladov
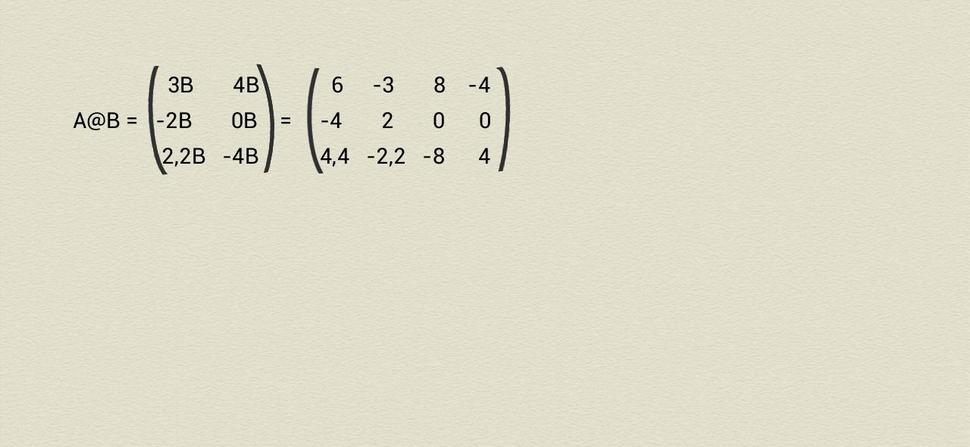
Nakoniec nám zostala definícia 2-súčinu, ktorý je daný obyčajným násobením matíc (budem predpokladať, že čitateľ je s ním oboznámený). Dá sa overiť, že oba definované súčiny ako aj všetky zavedené jedničky robia z množiny Mat naozaj 2-kategóriu a môžem teda teraz prejsť k definícii 2-kategórie orientovaných otvorených vrstevníc OOV.
V prvom rade zdôrazním, že OOV je geometrickou kategóriu, čím sa chce zhruba povedať, že jej prvky sa najlepšie znázornia obrázkami. Typický prvok kategórie OOV vyzerá ako štvorcový výrez z mapy nejakého pohoria, kde sú znázornené vrstevnice, čiže ako obrázok:
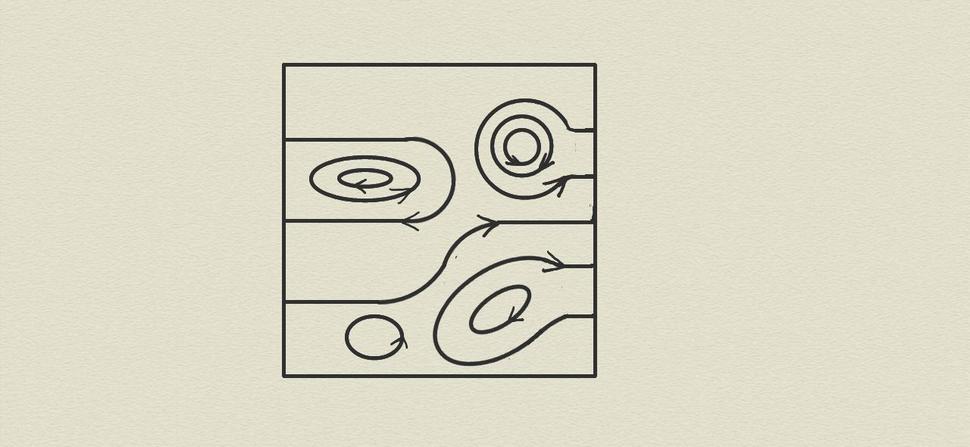
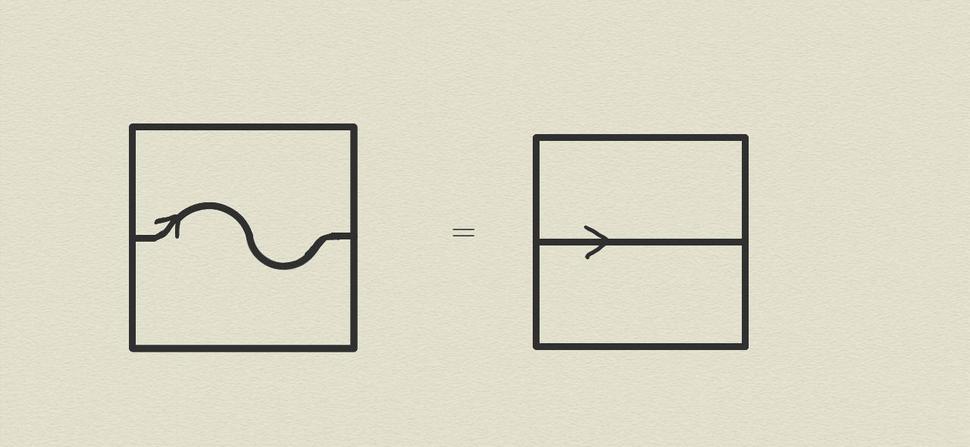
Všimnime si na Obr. 3 niekoľko dôležitých detailov, ktoré charakterizujú prvky kategórie OOV aj vo všeobecnosti: 1) Orientované čiary vpísané do štvorca sa nesmú navzájom pretínať a pokiaľ nie sú uzavreté (čiže zacyklené), tak môžu končiť iba na bočných stranách štvorca. 2) Konce nezacyklených čiar musia byť ukotvené na bočných stranách štvorca pod pravým uhlom a body ukotvenia musia rozdeľovať bočné strany štvorca na úsečky rovnakej dĺžky (napr. na obrázku 3 na ľavej bočnej strane štvorca sú ukotvené tri čiary v troch bodoch, ktoré rozdeľujú tú bočnú stranu na štyri časti o rovnakých dĺžkach). 3) Deformácie čiar, ktoré nevedú k ich pretínaniu, ani neposúvajú body ukotvenia ich koncov, či nenarušia pravé uhly ukotvenia, nemenia daný prvok kategórie OOV. Napríklad dva zdanlivo rôzne prvky na Obr. 4 zodpovedajú v skutočnosti tomu istému prvku OOV, keďže sú na seba prevediteľné dovolenými deformáciami čiar.
1-súčin v 2-kategórii je úplný (tj. nie iba čiastočný), čomu zodpovedá fakt, že v OOV je jediná 1-jednička. Tento 1-súčin je ilustrovaný na Obr. 5
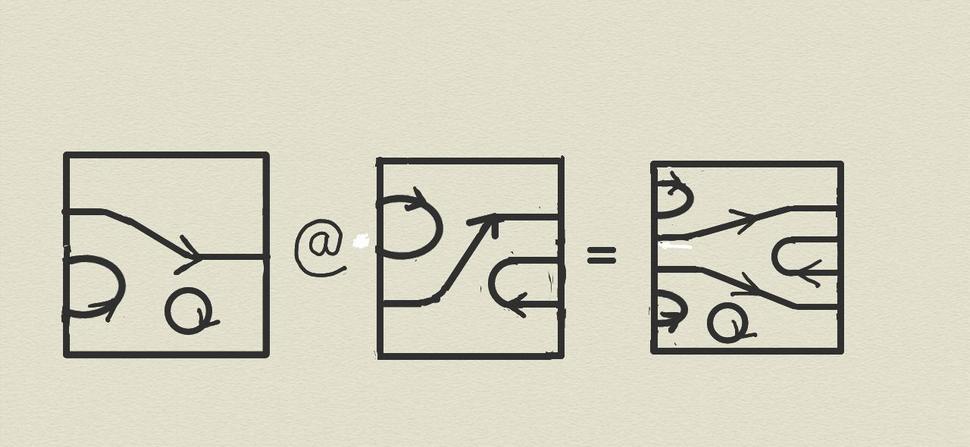
Ilustrovaný 1-súčin je vo všeobecnosti získaný položením pravého súčiniteľa hore na ľavý štvorec a následným vertikálnym “stľapčením” takto získaného stojaceho obdĺžnika na štvorec.
2-súčin prvkov 2-kategórie OOV je ilustrovaný na Obr. 6
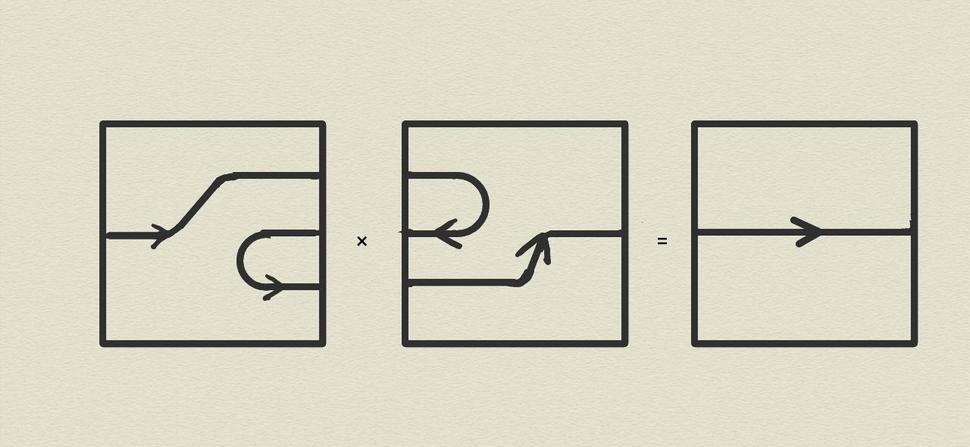
Zdôraznime, že 2-súčin je iba čiastočný; možno vynásobiť dva súčinitele iba v prípade, keď počet i orientácia končiacich otvorených čiar na pravej strane ľavého súčiniteľa súhlasí s počtom i orientáciou končiacich čiar na ľavej strane pravého súčiniteľa. Ak je tomu tak, tak 2-súčin sa získa priložením ľavého boku pravého súčiniteľa k pravému boku ľavého štvorca a následným horizontálnym “stľapčením” takto získaného ležiaceho obdĺžnika na štvorec.
Nakoniec nám zostalo popísať 2-jedničky v 2-kategórii OOV:
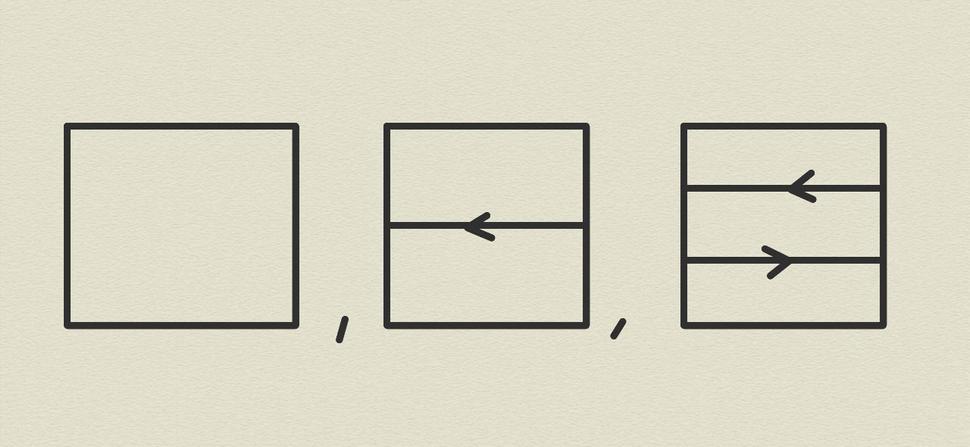
Zvládli sme teda podrobné definície geometrickej 2-kategórie OOV ako aj algebraickej 2-kategórie Mat a na budúcom rýdzo matematickom blogu o štyri týždne sa budem venovať konštrukcii 2-funktorov medzi týmito 2-kategóriami.






