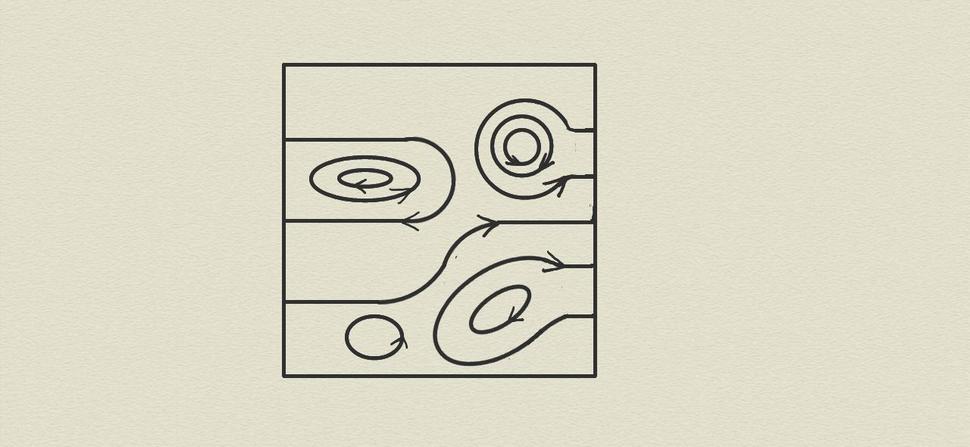
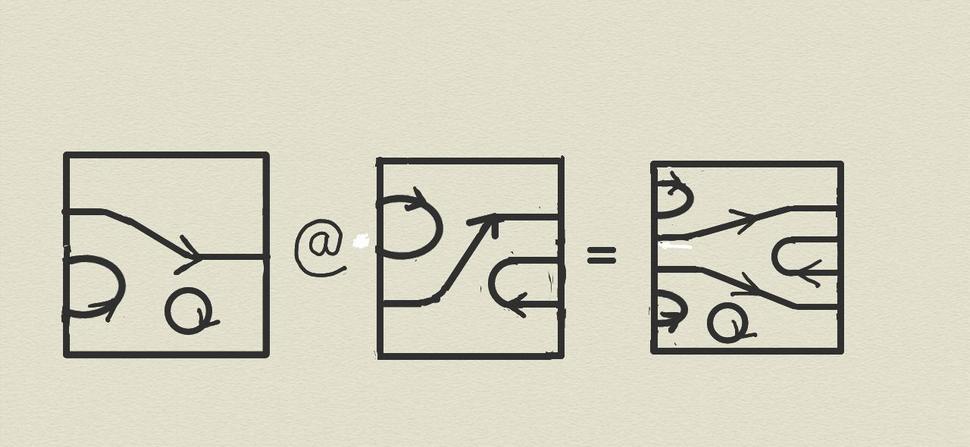
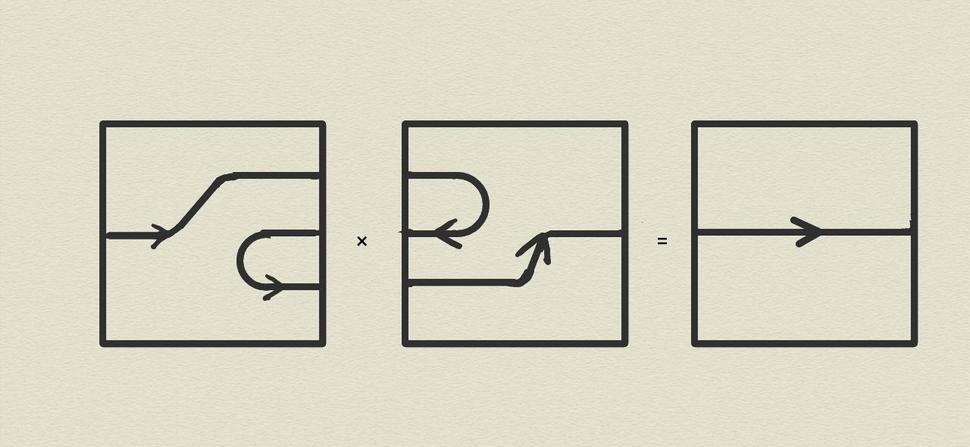
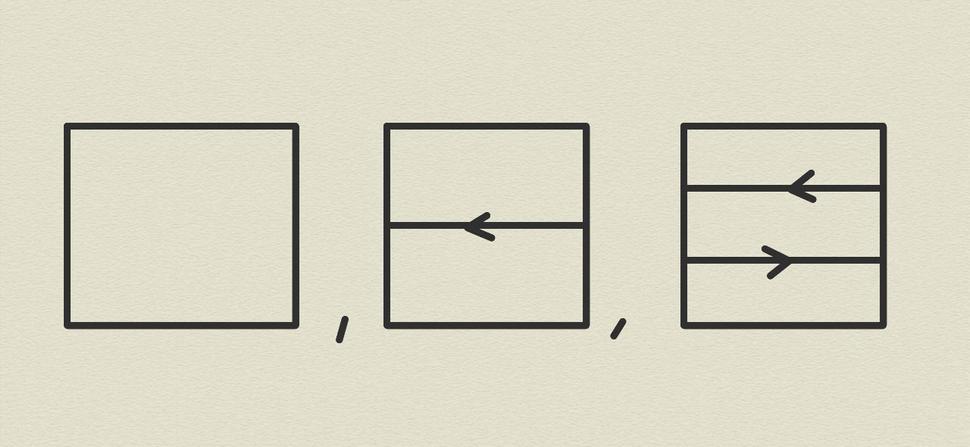
Pripomeniem, že v prvej časti tohoto blogu sme definovali topologickú kvantovú mechaniku ako zachovávajúce zobrazenie (nazývané v tomto kontexte 2-funktor) z geometrickej 2-kategórie OOV do algebraickej 2-kategórie Mat. Pripomeňme si štruktúru 2-kategórie OOV; jej prvky sú štvorce s vpísanými orientovanými čiarami ako na Obr.1, jej 1-súčin a 2-súčin sú ilustrované na Obr.2 a Obr.3 a jej 1-jedničky a 2-jedničky sú znázornené na Obr.4
Pripomeňme ešte, že prvky 2-kategórie Mat sú matice reálnych čísel s ľubovoľnými počtami riadkov i stĺpcov ako napr. na Obr.5, 2-jedničky v Mat sú štvorcové jednotkové matice označené ako En ( E1 je pritom zároveň 1-jedničkou), 2-súčin je daný obyčajným násobením matíc a 1-súčin tzv. direktným násobením @ ilustrovaným na Obr.6.
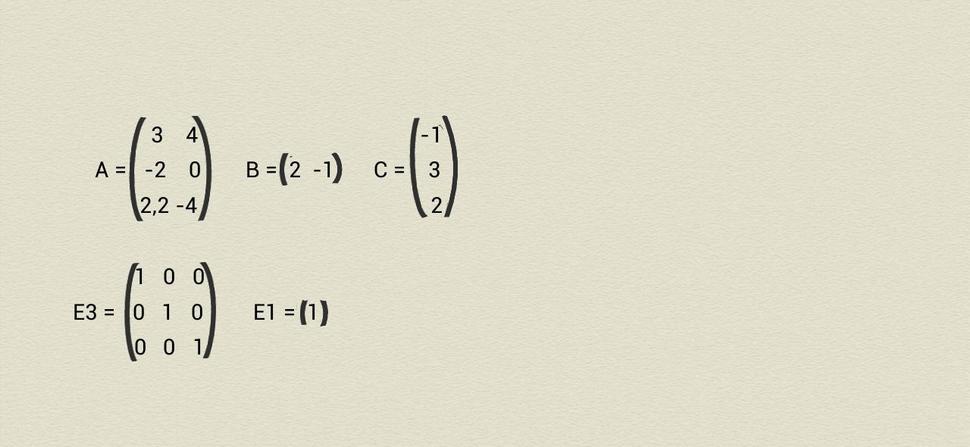
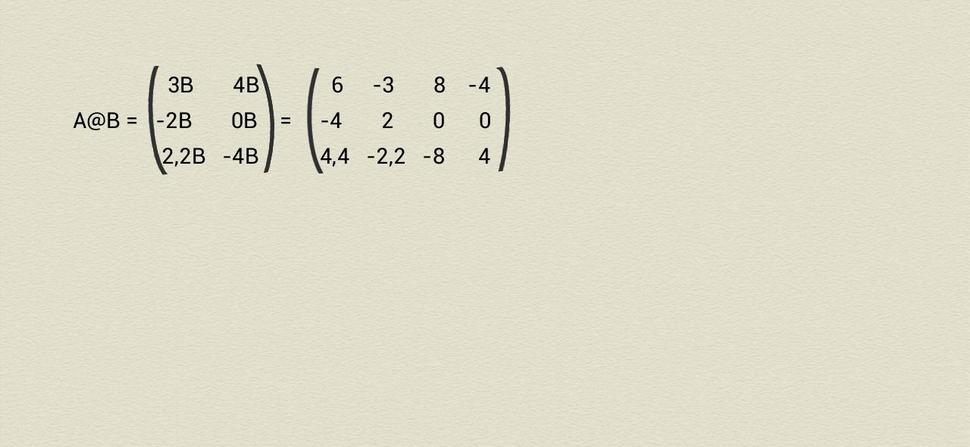
Naším bezprostredným cieľom je nájsť príklad 2-funktora F, ktorý každému obrázku z OOV priradí niektorú maticu Mat , pričom zachová štruktúru 2-kategórie. To predovšetkým znamená, že F priradí každej 2-jedničke z OOV niektorú z jednotkových matíc En (pričom prázdnemu štvorcu ako jedinej 1-jedničke 2-kategórie OOV priradí nutne E1 ako jedinú 1-jedničku 2-kategórie Mat) a každým dvom štvorcom a,b s vpísanými čiarami priradí nejaké matice F(a), F(b) tak, aby platili obidva nasledujúce vzťahy
F(a@b)=F(a)@F(b), F(a⨯b)=F(a) × F(b)
Vyjadrené slovami to znamená, že 2-funktor F zachováva aj 1-súčin @ aj 2-súčin × .
Skôr ako pristúpime k samotnej konštrukcii 2-funktora F, je dobré si uvedomiť, že zachovávajúce zobrazenie z nejakej štruktúry S do nejakej inej štruktúry T nemusí zachovávať “všetko”. Ak zachováva "všetko", tj. stotožní celú štruktúru S s celou štruktúrou T, hovorí sa mu izomorfizmus, ale vo všeobecnosti zachovávajúce zobrazenie F nestotožní S s T úplne. Napríklad sa môže stať, že hoci zachovávajúce zobrazenie zo samej svojej definície pôsobí na celú štruktúru S, jeho obraz môže byť iba časťou štruktúry T. Môžeme teda povedať, že keď si prezrieme podrobne štruktúru T nájdeme v nej časť, ktorá vyzerá ako celá štruktúra S? Ani toto nie je vždy pravda! Vo všeobecnosti nájdeme v T iba časť, ktorá vyzerá ako aproximácia celej štruktúry S! Objasnime si tieto trochu čudne vyzerajúce reči na dvoch príkladoch:
1) Predstavme si, že niekde na rovníku sa nachádza peň po čerstvo odpílenom strome, na priereze ktorého vidno štruktúru T perfektne kruhových letokruhov. Štruktúra S nech je lopta zavesená na niti presne nad stredom pňa. Nech zobrazenie z S do T je priemet každého bodu lopty na peň uskutočnený na poludnie 21. marca, kedy Slnko stojí v zenite a lopta vrhá na peň svoj tieň. Ten tieň je presne kruhový a stotožnuje sa s jedným z letokruhov, preto považujeme takéto zobrazenie za zachovávajúce. Všimnime si jednak, že ten tieň vo všeobecnosti nezakrýva celý kruhový prierez pňa, ale iba jeho časť a zdôraznime taktiež, že ten kruhový tieň na pni je síce obrazom celej lopty, ale ten kruhový obraz je dvojrozmerný a teda zabúda jeden rozmer trojrozmernej sférickej lopty. Povedané inými slovami obraz celej lopty na pni je len istou aproximáciou štruktúry skutočnej lopty.
2) Predstavme si, že pred tridsiatimi rokmi sa manželský pár vydal na dovolenku do Tatier, ona tam fotila farebne a on točil na čiernobielu kameru. Samozrejme, zábery nasnímané starou analógovou kamerou neboli vtedy nič iného ako súslednosť okamžitých statických čiernobielych obrázkov (keď sa dobre pamätám taká kamera ich fotila 24 za sekundu), na každý jeden takýto okamžitý čiernobiely obrázok sa dá teda nazerať ako na časť čiernobieleho filmu. Poďme teda teraz zostrojiť zachovávajúce zobrazenie z množiny S farebných fotiek urobených manželkou do množiny T čiernobielych filmov manžela. Manželka vezme farebnú fotku, urobí si z nej čiernobielu fotokópiu (to je vlastne tá aproximácia v zmysle, že zabúda farby v množine S) a prezerá si na videu čiernobiele filmy manžela až kým neuvidí na obrazovke identický obrázok ako na svojej čiernobielej fotokópii. Vtedy stlačí PAUSE a svojej celej aproximatívnej fotke so zabudnutými farbami priradí týmto spôsobom časť filmu manžela so všetkými čiernobielymi detailami. Zachovávajúce zobrazenie v tomto prípade zobrazí celú farebnú fotku do časti čiernobieleho filmu, “zabudne” či “nerozlíši” pritom niektoré detaily tohoto celku (konkrétne zabudne farby, alebo, inak povedané, nerozlíši modrú farbu od červenej), pričom však presne vystihne časť čiernobieleho filmu, do ktorej pôvodne farebnú fotku zobrazí.
Pripomeňme si, že topologická kvantová mechanika je 2-funktor zobrazujúci 2-kategóriu OOV do 2-kategórie Mat. Dá sa ukázať, že tento 2-funktor nemôže byť izomorfizmom, nutne teda niečo zabúda z 2-kategórie OOV a zobrazí iba istú aproximáciu OOV ako celku do časti 2-kategórie Mat. Dám teraz konkrétny príklad takéhoto 2-funktora, ktorý nazvem F3.
Časť 2-kategórie Mat, do ktorej náš 2-funktor F3 zobrazuje 2-kategóriu OOV, je množina Mat3 všetkých matíc, ktorých počet riadkov ako aj počet stĺpcov je nejaká mocnina čísla 3. Napr. každá matica, ktorá má tri riadky a jeden stĺpec, alebo má deväť riadkov a dvadsaťsedem stĺpcov patrí do množiny Mat3, keďže číslo jeden je nultá mocnina troch, tri je prvá mocnica, deväť je druhá a dvadsaťsedem je tretia mocnina troch. Naopak matica s tromi riadkami a piatimi stĺpcami nepatrí do Mat3.
Každý prvok Mat3 (s výnimkou E1) sa dá istým spôsobom “vygenerovať “ z istých dobre zvolených šiestich prvkov e1,e2,e3,f1,f2,f3 ako je to znázornené pre prípad matice M na nasledujúcom obrázku:
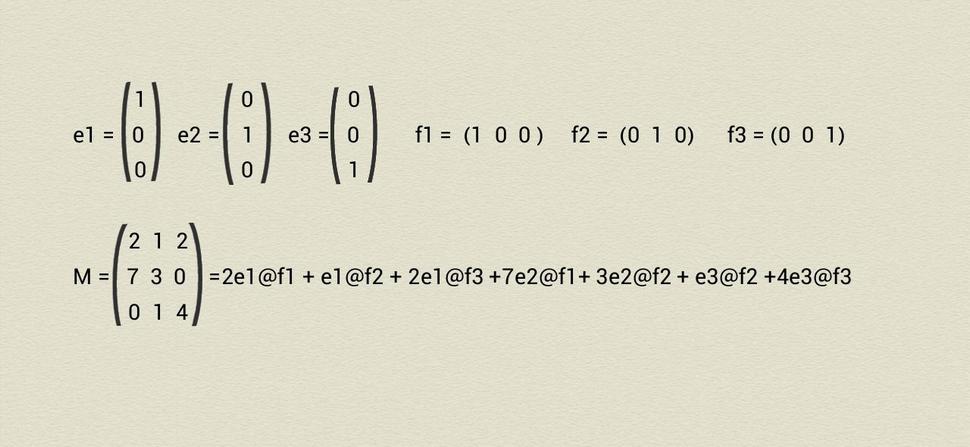
Všimnime si, že šesť tzv. matíc-generátorov e1,e2,e3,f1,f2,f3 generuje maticu M jednak pomocou direktného súčinu @ ale tiež pomocou sčítania matíc a ich násobenia reálnymi číslami. Tieto operácie sčítania či násobenia reálnymi číslami nemajú analógy na strane 2-kategórie OOV, 2-funktor F3 teda prenáša klasický svet OOV, kde sa nedá sčítať ani násobiť reálnym číslom na kvantový svet Mat3, kde sa sčítať a násobiť reálnym číslom dá. Toto je presne mágia kvantovania, keďže aproximácia štruktúry OOV sa prenesie z klasického sveta OOV do kvantového sveta Mat, kde sa môžu vykonávať operácie nemajúce pôvod v klasickom svete.
Poďme sa teraz pozrieť, čo priradí náš 2-funktor F3 2-jedničkám OOV nakresleným na Obr.4:

Znak Σ(i) znamená sčítanie cez všetky tri možné hodnoty indexu i (tj. i=1,2,3) a znak Σ(i,j) zasa sčítanie cez všetky možné hodnoty indexov i a j. Všimnime si, že na úrovni jedničiek funktor F3 zabúda orientáciu čiar vpísaných do štvorca, avšak na nasledujúcich obrázkoch 9 a 10 vidíme, že pri zobrazovaní všeobecnejších prvkov OOV si orientáciu pamätá:


Všimnime si niekoľko podrobností na obrázkoch 9 a 10, ktoré stoja za pozornosť. V prvom rade z formule F3(Obr.1) ľahko vydedukujeme spôsob, ako F3 priradzuje konkrétnu maticu každému štvorcu s vpísanými čiarami. Ďalej sa zdá, že 2-funktor F3 závisí na dvoch rôznych maticiach C a D zadaných na Obr.9, avšak pôsobenie F3 na ľavú aj pravú stranu rovnice na Obr.3 odhalí, že obyčajný súčin matíc C a D musí byť rovný jednotkovej matici (toto tvrdenie sa z recesie pripisuje Zorrovi, keďže horizontálne zlepenie dvoch štvorcov na ľavej strane dá písmeno Z, ktoré dovolenou deformáciou prejde na rovnú orientovanú čiaru na pravej strane.) Inými slovami, C a D sú navzájom inverzné matice a celý funktor F3 je teda kompletne zakódovaný v jednej jedinej invertibilnej matici C. Zdôrazňujem, že tento výsledok vyplýva z podmienok
F3(a@b)=F3(a)@F3(b), F3(a⨯b)=F3(a) × F3(b)
Všimnime si ďalej číslo 729 na pravej strane poslednej formuly Obr.10, v ktorom ľahko rozoznáme šiestu mocninu trojky a ktoré zodpovedá prítomnosti šiestich zacyklených vrstevníc na Obr.1. Vskutku, z obrázkov 9 a 10 ľahko vydedukujeme, že platí
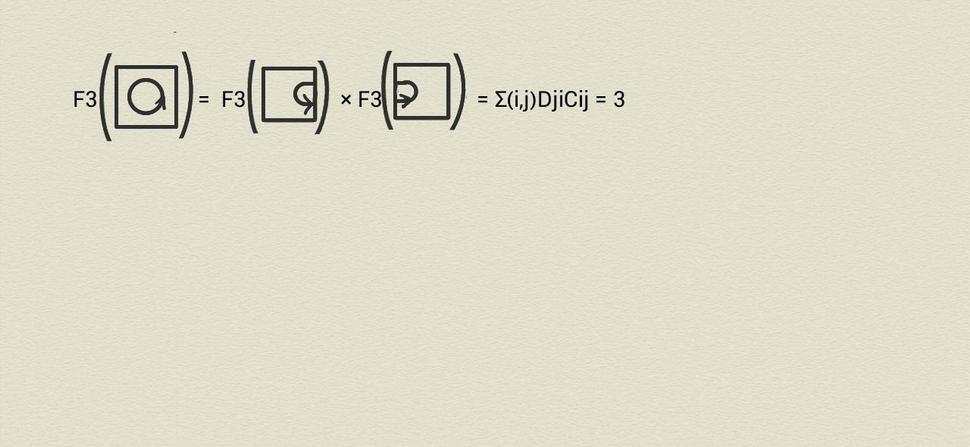
Dá sa vcelku ľahko ukázať, že nami skonštruované zobrazenie F3 je naozaj 2-funktor, a to dokonca jeden pre každú invertibilnú maticu C s tromi riadkami aj stĺpcami. Úplne analogickým spôsobom sa dá zostrojiť funktor Fn pre každé prirodzené číslo n, jeho obraz bude podkategória Matn pozostávajúca zo všetkých matíc, pre ktoré počet riadkov i stĺpcov je niektorou mocninou čísla n. Takýto funktor možno potom priradiť každej invertibilnej matici C s n riadkami i stĺpcami.
Aký je zmysel celej tejto konštrukcie? Zatiaľ hlavne matematicko-pedagogický. Ak jej chceme dať aj význam fyzikálny, musíme veci ešte trochu zozložitiť a uvažovať aj komplexné matice pričom od 2-funktora musíme chcieť aby zobrazoval obrázok s obrátenými šípkami na tzv. komplexne združenú maticu. I keď však nebudeme vchádzať do týchto ďalších detailov, môžeme zhruba tvrdiť, že 2-funktory z geometrickej 2-kategórie OOV do algebraickej 2-kategórie Mat sa dajú získavať kvantovaním klasických mechanických systémov s tzv. kompaktným fázovým priestorom a nulovým Hamiltoniánom. Práve posledná okolnosť odôvodňuje názov topologická kvantová mechanika. Matice ei definované na Obr. 7 tvoria pritom bázu tzv. Hilbertovho priestoru stavov, matica C je v komplexnom obore hermitovská a zadáva tzv. skalárny súčin na priestore stavov a nakoniec číslo priradené 2-funktorom uzavretému cyklu ako na Obr.11 sa interpretuje ako dimenzia Hilbertovho priestoru stavov. A na záver ešte poznámka pre znalcov: 2-kategoriálny jazyk v sebe automaticky zahrňuje aj tzv. druhé kvantovanie, takže náš 2-funktor dáva peknú geometrickú interpretáciu celej kinematiky kvantovej mechaniky.






