Trisekcia uhla
Podstatou tejto úlohy je rozdeliť ľubovoľný uhol na tri rovnaké diely, a to len pomocou pravítka a kružidla. Zaoberalo sa ňou mnoho geometrov, ale nikomu sa ju vo všeobecnosti nepodarilo – bez pripustenia určitých (dodatočných) pomôcok alebo postupov – vyriešiť.
(V niektorých špeciálnych prípadoch, pri vhodnej veľkosti uhla, vieme takto uhol rozdeliť na tri časti. Napríklad priamy uhol vieme, pomocou kružidla, rozdeliť na tri uhly po 60°).
Príčina tejto skutočnosti spočíva v tom, že analytické riešenie úlohy vedie k algebraickej rovnici tretieho stupňa, ktorej korene sa vo všeobecnosti nedajú zostrojiť pomocou pravítka a kružidla.
Nech je daný uhol α. [1]
Máme ho rozdeliť na tri rovnaké diely. Položme os „x“ do jedného z ramien daného uhla a opíšme okolo vrcholu „0“ kružnicu o polomere, ktorý budeme považovať za jednotku dĺžky. Obr.1.
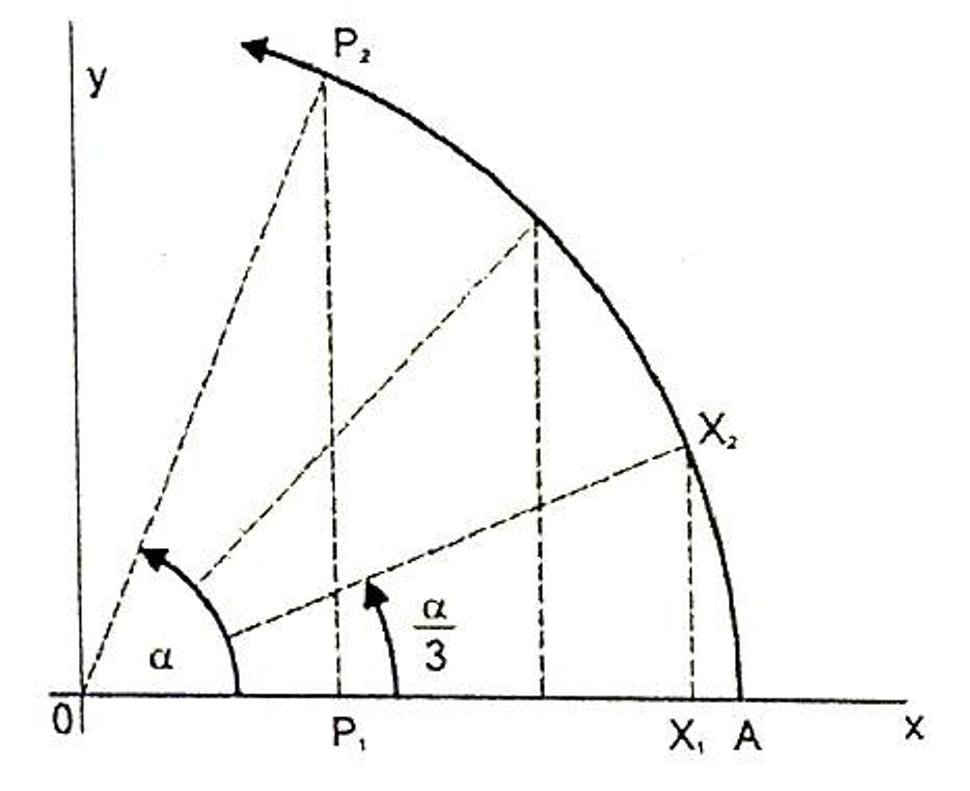
Súradnice bodu X(2) sú [cos (α/3), sin (α/3)]. Dané sú body „0“, P(1), P(2) a „A“. Hľadané body sú X(1) a X(2).
Úloha bude rozriešená, ak sa nám podarí zostrojiť bod X(1), t.j. dĺžku x = „0“X(1) = cos (α/3). Z goniometrie je známy vzťah
4.cos (α /3).cos (α/3).cos (α/3) – 3.cos (α/3) = cos α . (1)
[Tento vzťah dostaneme takto: Z Moivrovho vzorca vyplýva, že
cos 3β = 4.cos β.cos β.cos β – 3.cos β. Ak položíme β = α/3, dostávame vzťah (1).]
Číslo „x“ teda vyhovuje rovnici
4.x.x.x – 3.x - cos α = 0 . (2)
Ako už bolo povedané, korene rovnice (2) nevieme zostrojiť pomocou len pravítka a kružidla.
S pripustením vhodných pomôcok je úloha ľahko riešiteľná.
Trisekciu uhla možno zostrojiť napríklad pomocou pevnej paraboly y = x.x .
Už Archimedes (287? – 212 pr. n.l.) vedel, že ak pripustíme ďalšie konštrukčné pomôcky, je trisekcia uhla ľahko realizovateľná.
Majme naviac k dispozícii priamku „p“, na ktorej je nanesená pevná úsečka CD, napr. dĺžky 1, a pripusťme ako ďalšiu dovolenú operáciu „vsúvanie“ úsečky.
Potom bola už v staroveku známa táto konštrukcia:
Majme rozdeliť uhol A0B na tri rovnaké diely. Obr.2.
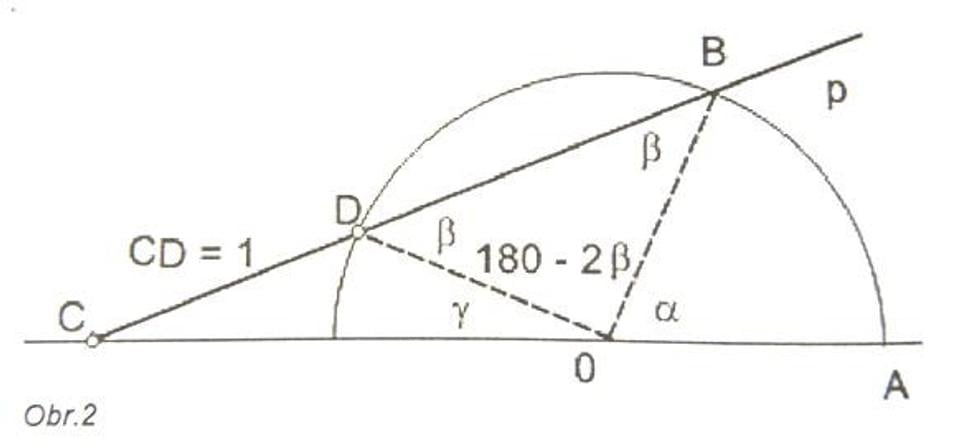
Zostrojme polkružnicu so stredom v začiatku „0“ o polomere „0“A = 1.
„Vsúvanie“ spočíva v tom, že priamku „p“ uvedieme do nasledujúcej (jednoznačne určenej) polohy: priamka „p“ prechádza bodom „B“ a úsečka CD má koncové body na priamke 0A, resp. na polkružnici ABD. Trojuholníky C0D a D0B sú rovnoramenné. Ďalej je β = 2γ , γ + 180º - 2β + α = 180º, teda γ = α/3. ([1], str. 352.)
Pseudo-trisekcia uhla
Majme uhol α, ktorý by sme chceli rozdeliť na tri rovnaké diely, no nevieme to urobiť.
Dôvody, ako je uvedené vyššie, sú známe.
Napodiv sa však zdá, že vieme rozdeliť - na tri rovnaké diely - uhol β, ktorý má „štruktúru“ β = (π - 3α), kde α < 60°. Obr.3. [2]
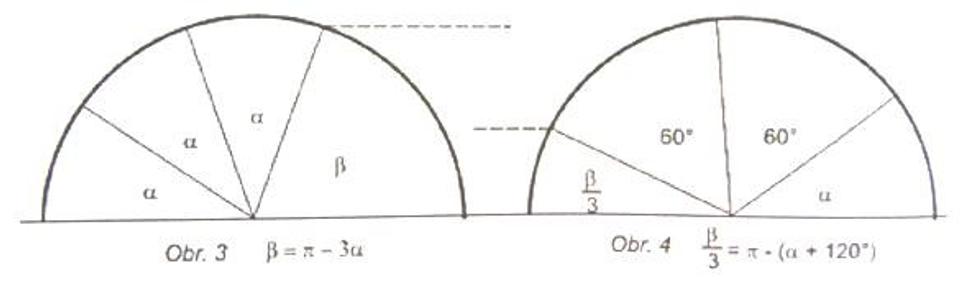
Uhol (π - 3α)/3 dostaneme ako rozdiel π – (α + 120°). Obr.4.
Uhol 120° „odkrokujeme po kružnici“ na dvakrát kružidlom, s nastaveným polomerom kružnice.
Dôkaz. Matematicky, jednoduchou úpravou sa presvedčíme, že naozaj platí vzťah
π – (α + 120°) = (π - 3α)/3 (3)
Majúc stále na zreteli „teóriu“ trisekcie uhla (uskutočnenej len pomocou pravítka a kružidla), je to trochu prekvapujúce zistenie.
Na prvý pohľad sa môže zdať, že je to spôsobené výnimočnou štruktúrou uhla β .
Síce nevieme priamo rozdeliť na tri rovnaké diely ľubovoľný uhol α , ale vieme vytvárať dvojice uhlov β a β/3, ktoré zodpovedajú konkrétnej voľbe uhla α є (0°, 60°), a to je nejaký pokrok.
V skutočnosti sa však nejedná o žiadnu, tobôž „regulérnu“ trisekciu uhla β, ale iba o umne vykonštruovaný geometrický postup, s použitím len pravítka a kružidla, ktorý označme pojmom pseudo-trisekcia.
Princíp pseudo-trisekcie uhla
Postup je založený na dvoch momentoch:
1. vieme jednoduchým spôsobom zhotoviť uhol 60°,
2. tento uhol možno vyjadriť ako súčet (zvoleného) uhla α a „doplnkového“ uhla γ. Pretože priamy uhol π tvorí trojica uhlov 60°, platí (obr.5)
π = 3(α + γ) = 3α + 3γ.
Zvolený uhol α a „doplnkový“ uhol γ sa nemusia nevyhnutne striedať tak, ako je to znázornené na obr.5.
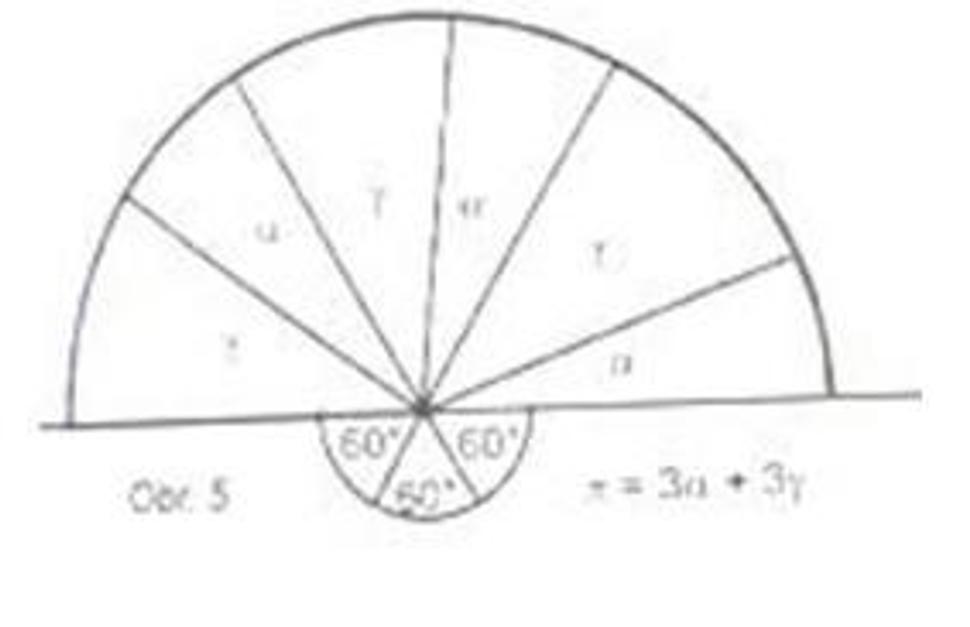
Ak všetky tri uhly α umiestnime vedľa seba (spolu 3α), vznikne tiež uhol 3γ – obr.6.
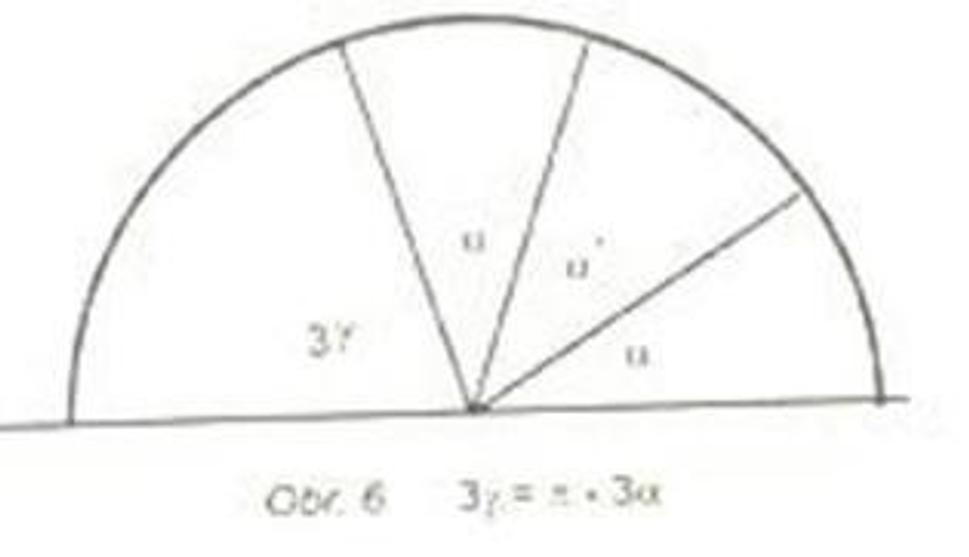
No, ak sa pozorne prizrieme obr.5, možno ho prekresliť na obr.7.
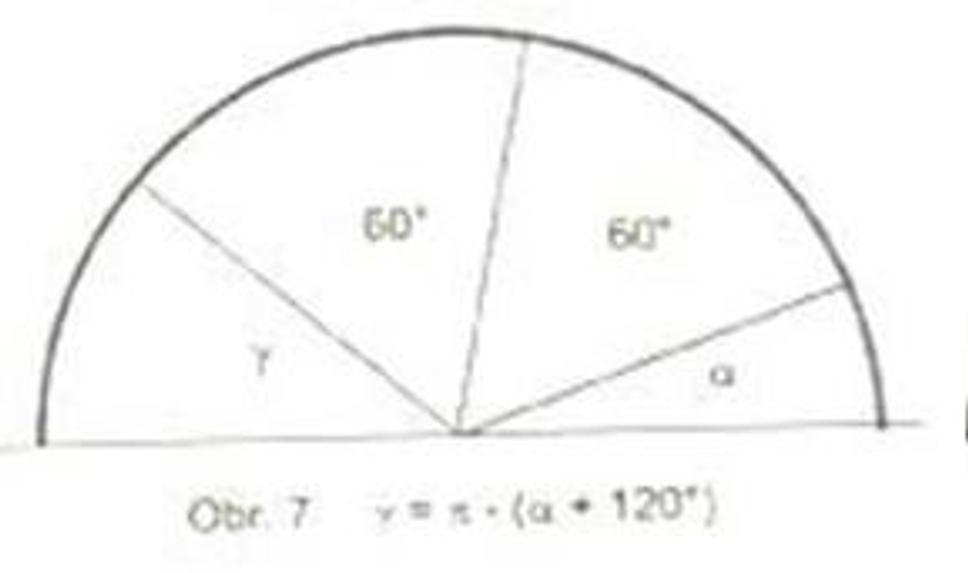
Z porovnania obr.6 a obr.7 je zrejmé, prečo platí vzťah (3).
Uhol γ(= β/3) je vždy tretinou uhla 3γ(= β)!
A pretože uhol γ je takým „doplnkovým“ uhlom k uhlu α, že spolu tvoria uhol 60°, veľkosť uhla γ je priamo podmienená voľbou uhla α a netreba ho určovať konštrukčným postupom podľa obr.7.
Pseudo-pentasekcia uhla
Analogický princíp možno využiť aj pri delení uhla na päť rovnakých častí. Volený uhol α však môže nadobúdať hodnotu len z intervalu (0°, 36°).
Potom uhol β má „štruktúru“ β = (π - 5α), kde α ˂ 36°. Päťkrát menší uhol γ je doplnkový uhol k súčtu uhlov α + 4.36°, aby vznikol priamy uhol π, [resp. doplnkovým uhlom k uhlu α, kde α + γ = 36°]. Teda
γ = π – (α + 4.36°)
Tiež platí
π – (α + 4.36°) = (π - 5α)/5 (4)
Uhol 36° je možné skonštruovať len pomocou pravítka a kružidla, keďže je týmto spôsobom možná konštrukcia pravidelného päťuholníka (založená na možnej konštrukcii uhla 72°).
Delenie uhla na sedem rovnakých častí, resp. na deväť rovnakých častí – ani prostredníctvom tohto triku – však nie je možné, pretože nevieme pomocou pravítka a kružidla zostrojiť uhly 2π/7 alebo 2π/9. Teda by sme nevedeli zostrojiť ani „doplnkové“ uhly γ = (2π/7 - α), resp. γ = (2π/9 - α).
Delenie uhla na šesť alebo osem rovnakých častí touto „metódou“ je naproti tomu možné, pretože 2π/6 = 60° a 2π/8 = 45°, a tieto uhly vieme zostrojiť.
Vo všeobecnosti možno konštatovať, že túto „metódu“ možno použiť len tam, kde vieme korektným spôsobom zostrojiť pravidelný n-uholník (napr. 17-uholník, 257-uholník, 65537-uholník).
Pramene:
[1] SCHWARZ, Š.: Základy náuky o riešení rovníc, Bratislava 1968
[2] CUDZIŠ, F.: Pseudo-trisekcia a pseudo-kvintasekcia uhla
Myšlienky a fakty, roč. 2008, ISBN 978-80-969282-9-3
Do pozornosti stálym čitateľom mojich článkov:
Vážení priatelia, v poslednej dobe dostávam do svoje e-mailovej schránky cufr@centrum.sk od facebooku zoznamy mien ľudí, ktorí by azda chceli so mnou komunikovať cez facebook. Za všetky ponuky na tento kontakt vám srdečne ďakujem, no (predbežne) zo - subjektívnych dôvodov - nechcem pobývať na facebooku, aj keď ponúka možnosť chatu. Preto každého, kto má záujem o nejaké doplňujúce informácie k mojim myšlienkam, alebo dokonca záujem o nejakú (aj jednorázovú) formu spolupráce so mnou, nateraz odkazujem na uvedený e-mailový kontakt. Dúfam, že vás to neurazí ani neodradí od vašich zámerov v súvislosti so mnou. Ďakujem vám za porozumenie.






