2.5 Všeobecná kozmodriftová rovnica a jej základné dôsledky
Analýza dôvodov objektívnej platnosti mechanického princípu relativity vedie logicky k tzv. „všeobecnej kozmodriftovej rovnici”.
Túto rovnicu odvodíme zo vzťahu (12n). Po roznásobení zátvoriek s druhými mocninami, prevedení všetkých členov na ľavú stranu a ich usporiadaní podľa mocnín tzv. „všeobecného” (resp. „zovšeobecneného”) kozmodriftu „ŵ”, dostaneme:
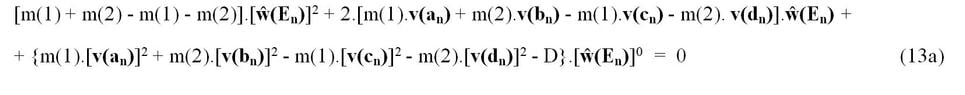
Koeficient pri druhej mocnine „ŵ” je evidentne rovný nule. Koeficient „A”, pri prvej mocnine „ŵ” – z fyzikálneho hľadiska predstavujúci zákon zachovania hybnosti pre zraz daných telies - je rovný nule len zdanlivo. A koeficient „B” – z fyzikálneho hľadiska predstavujúci zákon zachovania kinetickej energie pre zraz daných telies – je tiež rovný nule.
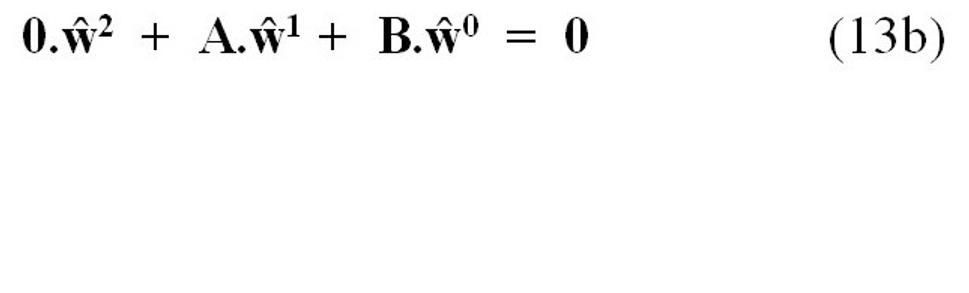
Všeobecná kozmodriftová rovnica prekvapuje tým, že špecifickým spôsobom „v sebe spája” dva dôležité fyzikálne zákony (či skôr zákonitosti) v oblasti mechaniky, a to zákon zachovania hybnosti a zákon zachovania kinetickej energie. A to čo ich spája, je – inerciálny pohyb súradnicovej sústavy ľubovoľnou rýchlosťou „ŵ”, ktorej veľkosť a smer ani nemusíme poznať.
Možno to niekoho prekvapí, ale poviem popravde. – Trvalo mi dobrých dvadsať rokov, kým som si uvedomil - zdanlivo banálny, v skutočnosti však veľmi podstatný – dôsledok platnosti všeobecnej kozmodriftovej rovnice (12n), resp. (13a):
Každá súradnicová sústava, v ktorej koexistujú zákon zachovania hybnosti a zákon zachovania kinetickej energie, je inerciálna, t.j. objektívne sa pohybujúca vlastným kozmodriftom.
Domysliac tento poznatok do dôsledkov, ak takúto koexistenciu predpokladáme všade vo vesmíre, musíme tiež predpokladať, že potom sa inerciálne pohybuje aj celý vesmír – ako jeden celok. V tzv. kozmoolovom modeli Univerza, ktorý je jednou z možných interpretácií fyzikálneho obrazu nášho sveta podľa teórie kozmodriftu, som tento celok nazval pojmom „kozmoola”. (Pozri www.kozmodrift.sk, 6. časť – Kozmoolový model Univerza.)
Alebo – v snahe poprieť pohyb vesmíru ako celku – musíme rátať s iným dôsledkom, totiž, že stav koexistencie zákona zachovania hybnosti a zákona zachovania kinetickej energie nie je všeobecným stavom; niekde platí a niekde nie. A to už by bol oriešok aj pre „kozmologickú fyziku” – a poriadny! Nikto z moderných „matematických fyzikov-kozmológov” na taký – v podstate banálny – dôsledok uznávaných poznatkov klasickej fyziky zrejme nepomyslel. A správnosť týchto poznatkov nie je možné poprieť, aj keby sa fyzik-neviem-kto a neviem-aký postavil na hlavu. Akurát by sa mu tak mohli len vysypať z batoha na chrbte všetky jeho tituly a ocenenia.
Pritom, argumentov podobného „kalibru”, existuje viacero.
2.5.1 Fyzikálny príspevok Fridricha Engelsa
Problém koexistencie zmienených dvoch zákonov zaujímal mnohých vysoko inteligentných ľudí, lebo viedol k otázke čo je objektívnou mierou mechanického pohybu a zákonite vznikol medzi nimi spor.
Fridrich Engels, ktorého v tejto súvislosti s obľubou spomínam, v článku „Miera pohybu. – Práca” [4] napísal: „neplodný“ spor, ktorý „trval vyše 40 rokov, a rozdelil matematikov v Európe do dvoch nepriateľských táborov, až napokon d´Alembert svojou Úvahou o dynamike (1743) rozriešil doslova suverénnym spôsobom túto zbytočnú škriepku o slová; lebo o nič iné nešlo“. (Suter, cit. d., s. 366).
A pokračoval: „Zdalo by sa však, že sporná otázka jednako nemôže tak celkom spočívať v zbytočnej škriepke o slová, keď ju vytýčil taký mysliteľ ako Leibniz proti takému mysliteľovi, ako bol Descartes, a keď človeka ako Kanta zaujímala natoľko, že jej venoval svoje prvé dielo, dosť objemný zväzok. A naozaj, ako je to len možné, že pohyb má dve vzájomne si protirečiace miery, takže raz je úmerný rýchlosti a raz štvorcu rýchlosti?” … „Ide o to, aby sme pochopili, prečo má pohyb dve miery, teda o vec, ktorá je vo vede práve tak neprípustná ako v obchode.”
Na základe vlastnej analýzy problematiky, dospejúc k názoru, že objektívnou mierou pohybu je kinetická energia, napísal:
„Ukazuje sa teda, že spor Leibniza s karteziánmi už vonkoncom nebol nejakou obyčajnou škriepkou o slová a že d´Alembertovo „suverénne riešenie“ v skutočnosti nič nevyriešilo. D´Alembert sa nemusel so svojimi tirádami o nejasnosti názorov svojich predchodcov unúvať, lebo je práve taký nejasný ako oni. A naozaj, pokiaľ sa nevedelo, čo sa stane so zdanlivo strateným mechanickým pohybom, musela zostať otázka nejasná. A pokiaľ matematickí mechanisti ako Suter zostávajú zaťato v zajatí štyroch stien svojej špeciálnej vedy, zostávajú rovnako nejasní ako d´Alembert a budú nás musieť odbiť prázdnymi a protirečivými frázami.”
Poznanie, že „správnou” mierou mechanického pohybu je kinetická energia, nerieši otázku dôvodu existencie a skutočného významu hybnosti mechanického pohybu.
2.5.2 Fyzikálny príspevok Emmy Noerthovej
Emmy Noerthová (1882 - 1935) bola významná nemecká matematička. Preslávila sa vetou, ktorá hovorí o súvislosti medzi symetriou a zákonmi zachovania.
Čo sa týka symetrie, vo fyzike je prírodný zákon symetrický vtedy, ak na ňom môžeme vykonať nejakú transformáciu a aj po tejto transformácii budú výsledky konkrétneho merania, vykonaného na tomto fyzikálnom systéme, rovnaké ako predtým.
Zákony zachovania sú zákony vyjadrujúce časovú nemennosť tzv. zachovávajúcich sa veličín v izolovaných sústavách . Vyplývajú zo skúsenosti o nemennosti istých fyzikálnych veličín. Delia sa na „absolútne”, ktoré platia pri akejkoľvek interakcii častíc sústavy a na zákony platné len v obmedzenej oblasti javov. Za „absolútne” považuje moderná fyzika napr. zákon zachovania hmotnosti (objavený chemikmi), energie, hybnosti, momentu hybnosti a ťažiska, a tiež zákon zachovania náboja. (Wikipédia)
Z pohľadu teórie kozmodriftu, vo výpočte „absolútnych” fyzikálnych zákonov tu chýba najfundamentálnejší zo zákonov zachovania, a to zákon zachovania stavu. Ten hovorí len toľko, že objektívna realita (všetok pohyb, všetky deje, ich suma) predstavuje fyzikálny systém, plynule prechádzajúci nekonečným radom ekvivalentných (navzájom rovnocenných) stavov. Podľa toho sa všetko v objektívnej realite zachováva. Nič nemôže pribudnúť ani sa nič nemôže stratiť. Pravda, platí to za predpokladu o objektívnej povahe (transvektorovej) kinetickej energie.
Ale, aby som sa vrátil k práci Emmy Noerthovej. - Populárne povedané, v zmysle teórie symetrií, sa fyzikálna veličina – hybnosť telesa – zachováva (osobitne) pri jeho posunutí (bez interakcie) v priestore. Podobne, energia – špeciálne (relatívna) kinetická energia - telesa sa zachováva (osobitne) pri jeho „posunutí” v čase.
Hoci má Noerthovej myšlienka o súvislosti medzi (matematickou) symetriou a (fyzikálnymi) zákonmi zachovania racionálne jadro, v konečnom dôsledku akoby predstavovala paralelu „d´Alembertovho suverénneho riešenia” v jeho diele „Úvaha o dynamike” (1743), ako o ňom svojho času písal Fridrich Engels. Dôsledné a „konečné” fyzikálne zdôvodnenie koexistencie zákona zachovania energie mechanického pohybu a zákona zachovania hybnosti tohto pohybu z myšlienky Emmy Noerthovej – nevyplýva.
S určitou dávkou benevolencie by sa dalo povedať, že však – ak sa hmotný objekt pohybuje vo (povedzme Einsteinovom „exotickom”) fyzikálnom kontinuu, totiž v „časopriestore” – pohybuje (či posúva) sa zároveň aj vzhľadom na priestor aj v čase. Ale, predosielam, vonkoncom to nezodpovedá objektívnej realite. Podľa záverov teórie kozmodriftu totiž nič také ako „hybnosť” objektívne neexistuje.
Áno, z matematického hľadiska možno definovať (matematickú, okamžitú) hybnosť ako súčin hmotnosti daného objektu a jeho okamžitej rýchlosti. Rýchlosti – ale akej? Je evidentné, že máme na mysli rýchlosť, z fyzikálneho hľadiska veličinu (len) relatívnej povahy, pretože ju určujeme vzhľadom na subjektívne zvolenú súradnicovú sústavu. Pri vyšších hodnotách pozorovanej rýchlosti daného hmotného objektu sa však (matematická) hybnosť zrazu začne (fyzikálne) meniť na akúsi „relativistickú” hybnosť. A až na túto sa vraj dôsledne vzťahuje zákon zachovania hybnosti. Tým ale problémom s hybnosťou nie je koniec.
Ak sa na vec pozrieme z druhej strany, fyzikálna situácia vyzerá podstatne ináč.
Ako som už konštatoval, pri problematike vzťahu s vektormi a transvektormi, už len pri zohľadnení „astronomického” pohybu Zeme vzhľadom na Slnko (rýchlosťou cca 30 km/s), existuje výrazná asymetria medzi hodnotami rýchlostí „bežných” pozemských pohybov a medzi rýchlosťou – trebárs - „astronomického” pohybu Zeme, ktorý možno považovať za istý predobraz vlastného kozmodriftu Zeme. Ibaže – opäť predosielam – ak hovorím o pohybe Zeme v okolí Slnka ako o „astronomickom” pohybe, potom musím o vlastnom kozmodrifte Zeme (vo svetovom priestore) hovoriť ako o jej „kozmologickom” pohybe. Mnoho fyzikálnych momentov nasvedčuje tomu, že vlastný kozmodrift Zeme je o niekoľko rádov rýchlejší ako jej „astronomický” pohyb (cca o štyri rády).
Pri takom usporiadaní objektívnej reality by nemal existovať rozdiel medzi „bežnou” a relativistickou hybnosťou pohybujúcich sa telies. Ak však prihliadneme na objektívnu existenciu vlastného kozmodriftu Zeme, resp. na existenciu akéhosi všeobecného (všetko materiálne zasahujúceho) kozmodriftového pohybu, ktorý je pôvodcom veľmi výraznej fyzikálnej asymetrie v našom svete (v celom vesmíre), zistíme, že žiaden podobný problém neexistuje. Z fyzikálneho hľadiska je hybnosť len nepochopeným „odrazom” jedinej objektívnej miery mechanického pohybu, totiž – transvektorovej kinetickej energie.
2.5.3 Obraz sveta, kde by bola energia úmerná tretej mocnine rýchlosti pohybu
Pri formovaní základov teórie kozmodriftu som už dávno tušil podstatu vzťahu kinetickej energie a hybnosti, a to práve v súvislosti so všeobecnou kozmodriftovou rovnicou.
Tvar všeobecnej kozmodriftovej rovnice, z ktorej vyplýva viacero veľmi dôležitých dôsledkov pre fyziku, je podmienený (dalo by sa povedať „tak trochu banálnym”) faktom, totiž, že energia mechanického pohybu závisí od druhej mocniny jeho rýchlosti. Ale to ešte nie je všetko.
Rovnako dôležitý je pritom aj fakt, že „matematický aspekt” relatívneho priestoru aj objektívneho priestoru sú identické. Obidva sa vzťahujú na nehmotné pojmy (napr. čas trvania, priestorová vzdialenosť) alebo iné abstraktné predstavy (rýchlosť, zrýchlenie a pod.). Preto všetky základné vzťahy, ako ich poznáme v klasickej mechanike, majú rovnaký tvar v (relatívnom) pozorovateľnom priestore i v (objektívnom) kozmodriftovom priestore.
Uvedomil som si, že keby bolo usporiadanie objektívnej reality (sveta) iné – napr. také, že energia mechanického pohybu by bola funkciou tretej mocniny jeho rýchlosti – priebeh nám dôverne známych dejov by musel vyzerať ináč.
V takom prípade by rovnica (12n) musela mať tvar
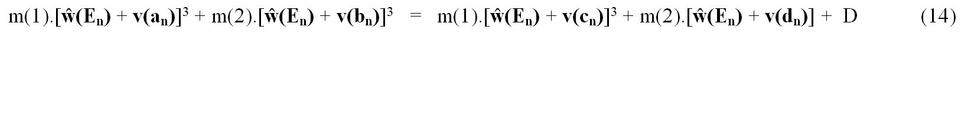
a z nej vyplývajúca všeobecná kozmodriftová rovnica by musela mať tvar
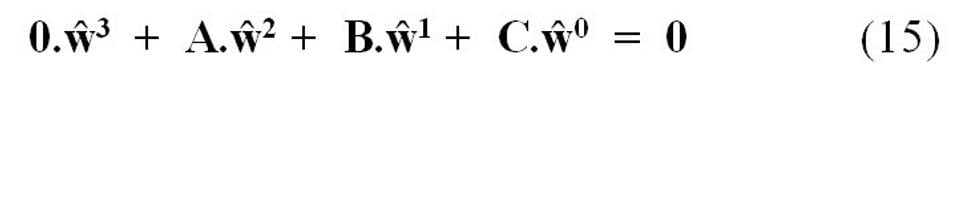
Pre jednotlivé koeficienty A, B, C pri mocninách „ŵ” platí:
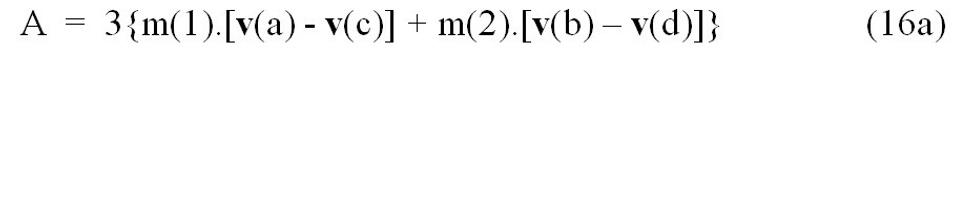
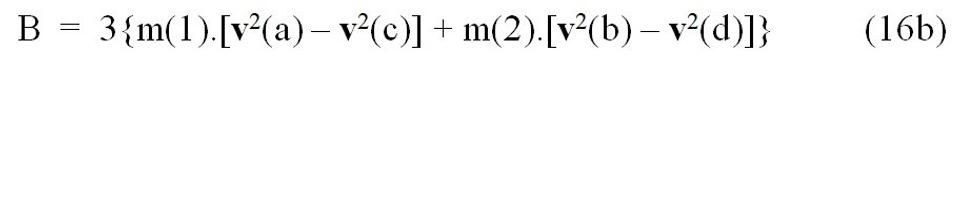
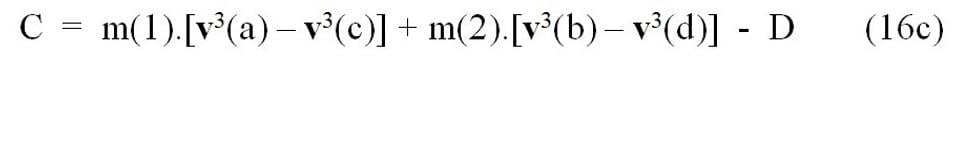
Svet, popísaný rovnicami (14) až (16), by musel naozaj fungovať diametrálne odlišným spôsobom od nášho sveta, ako ho poznáme. - Pohyb hmotných objektov by podliehal súčasne trom rôznym zákon zachovania. A je otázka, či by v takomto svete vôbec existoval (resp. mohol existovať aspoň teoreticky) fenomén zotrvačnosti.
Uvažovať podobným spôsobom, Galileo Galilei jednoducho – ako sa hovorí - „nemal nárok”. Nemohol objasniť príčinu fyzikálneho fenoménu, akým je zotrvačnosť pohybu. Ani nečudo, ak si uvedomíme, že zotrvačnosť pohybu nie je hodnoverne zdôvodnená dodnes. A to aj napriek viacerým prelomovým objavom vo fyzike, ku ktorým táto veda dospela v priebehu nasledujúcich storočí.
Pokračovanie.
Do pozornosti stálym čitateľom mojich článkov:
Vážení priatelia, v poslednej dobe dostávam do svoje e-mailovej schránky cufr@centrum.sk od facebooku zoznamy mien ľudí, ktorí by azda chceli so mnou komunikovať cez facebook. Za všetky ponuky na tento kontakt vám srdečne ďakujem, no (predbežne) zo - subjektívnych dôvodov - nechcem pobývať na facebooku, aj keď ponúka možnosť chatu. Preto každého, kto má záujem o nejaké doplňujúce informácie k mojim myšlienkam, alebo dokonca záujem o nejakú (aj jednorázovú) formu spolupráce so mnou, nateraz odkazujem na uvedený e-mailový kontakt. Dúfam, že vás to neurazí ani neodradí od vašich zámerov v súvislosti so mnou. Ďakujem vám za porozumenie.






