Pred nástupom prvých štátnych útvarov a pred rozvojom modernej matematiky sa ľudia v praveku ocitli pred výzvou: ako vyjadriť a pracovať s číslami, a to bez moderných číselných systémov, ktoré nám sú dnes také samozrejmé? Prirodzeným prostriedkom na vyjadrenie počtu boli prsty na rukách a nohách, či už v podobe ukazovákov, prostredníkov, alebo akejkoľvek inej kombinácie. Táto metóda počítania na prstoch bola intuitívna, ale mala svoje obmedzenia, pretože bola obmedzená na čísla menšie ako dvadsať, čo bolo značne nepraktické, najmä pre rozsiahlejšie počítanie.
Nepozičné číselné systémy:
S postupným rozvojom spoločnosti a potrebou efektívnejšieho spôsobu vyberania daní a evidovania majetku sa stalo zrejmým, že systém zárezov do stien jaskýň a hlinených doštičiek už nestačí. Pokiaľ mala spoločnosť udržať prehľad o majetku a platbách, potrebovala niečo viac sofistikovaného. Prvé kroky viedli k vzniku symbolov a značiek, ktoré boli použité na označenie určitého počtu. Rôzne civilizácie vytvorili svoje vlastné systémy zápisu. Napríklad Mayovia používali bodky pre jednotky, vodorovné čiary na pätičke pre desiatky a zvislé čiary pre dvadsiatky. Tieto systémy sa na nazývali nepozičnými nakoľko nezáležalo na akej pozícii ten, ktorý znak leží. Mohli ste ich napísať v akomkoľvek poradí alebo aj zvisle.

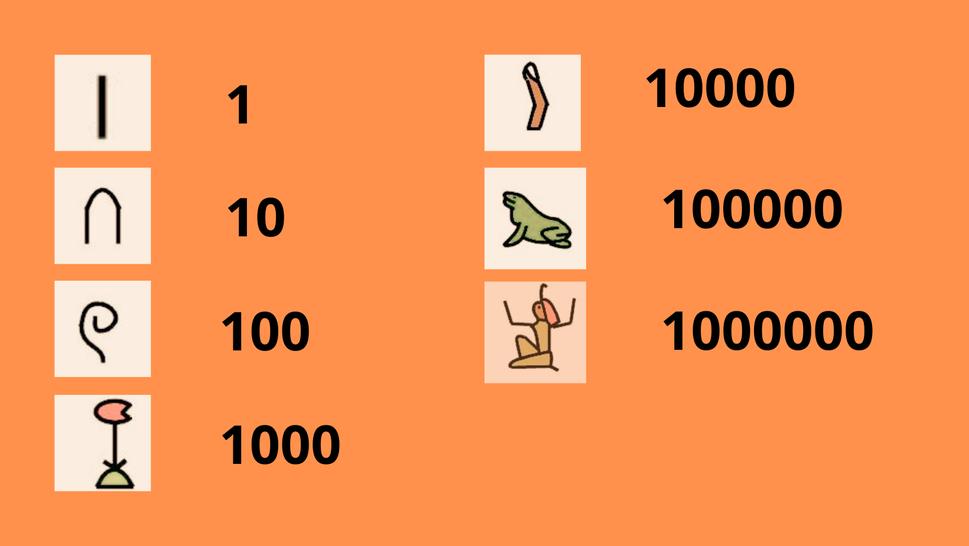
Egyptské číslice mali hieroglyfy pre rôzne rady.
Rimania prišli s používaním písmen pre reprezentáciu čísel.

Hoci tieto systémy slúžili svojmu účelu, mali zásadné nedostatky. Boli nepozičné, čo znamená, že hodnota číslice nezávisela na jej pozícii. Tým pádom bolo ťažké vykonávať matematické operácie a reprezentovať väčšie čísla. Zvýšená potreba nových znakov pre vyjadrenie väčších čísel bola komplikáciou, a tak napríklad číslo 16326 by u Rimanov vyžadovalo znova a znova opakovať rovnaké písmená:


Ďalším problémom bola neschopnosť reprezentovať zlomkové čísla a záporné hodnoty. Nepozičné systémy boli obmedzené na celé čísla, čo sťažovalo prácu s abstraktnejšími matematickými konceptmi. Aritmetické operácie, ako sčítanie, odčítanie, násobenie a delenie, boli ťažké, a vykonávanie zložitejších matematických úloh bolo takmer nemožné.
Historickým nástrojom, ktorý pomáhal s aritmetickými operáciami v nepozičných číselných systémoch, bol Abakus. Abakus bol tvorený rámom so šnúrkami alebo drôtmi, na ktoré boli navlečené korálky alebo iné počítacie jednotky. Jeho využitie v nepozičných číselných systémoch bolo veľmi užitočné na vykonávanie základných matematických operácií, ako sú sčítanie, odčítanie, násobenie a delenie. Avšak pre delenie bolo potreba skúseností a cviku, a používanie abakusu vyžadovalo značné zručnosti.
Pozičné číselné systémy:
Prechod k pozičným číselným systémom priniesol zásadnú zmenu. V týchto systémoch je hodnota každej číslice určená jej pozíciou v rade symbolov. Každá pozícia má svoju váhu v celkovom čísle v závislosti od svojej pozície. To znamená, že jednotky sa píšu ako posledné, desiatky druhé od konca, stovky tretie a tisíce štvrté a tak ďalej. Tím sa umožnilo oveľa jednoduchšie a flexibilnejšie zápis čísel.
Jedným z kľúčových prvkov pozičných číselných systémov bol symbol nuly. Symbol nuly umožnil rozlíšiť medzi rôznymi hodnotami a znamenal zlom vo vývoji matematických systémov. Aby sme mohli napísať číslo 101, musí existovať symbol nuly na druhej pozícii pre desiatky. V opačnom prípade by sme dostali číslo 11. Symbol nuly bol zásadný pre matematiku, a bez neho by nebolo možné reprezentovať mnoho čísel a vykonávať zložité operácie.
V pozičných sústavách závisí od pozície číslic. Každá cifra má svoju váhu, čo znamená, že na rôznych pozíciách v čísle reprezentuje rôzny počet. Pozícia dáva číslicu váhu, a zmenou pozície meníme hodnotu číslice. Napríklad číslo 248 sa skladá z 2 stoviek, 4 desiatok a 8 jednotiek. Každá pozícia určuje, koľkokrát daná cifra má danú váhu.

Každá číselná sústava má svoj základ, čo je počet cifier, ktoré sú v nej k dispozícii. Väčšina bežných sústav má desiatkový základ, čo znamená, že má 10 cifier od 0 do 9. Existujú však aj iné sústavy, ako dvojková, ktorá má 2 cifier (0 a 1), alebo šestnástková, ktorá má 16 cifier (0-9 a A-F).
Dôležitým aspektom pozičných číselných systémov je fakt, že na každej pozícii môže byť použitá každá cifra. Každá pozícia cifre priraďuje váhu, čo umožňuje ľahko vyjadriť rôzne hodnoty. Zmenou pozície číslice meníme jej váhu, a tým aj hodnotu celého čísla.
Kľúčovú úlohu v prechode na pozičné číselné systémy v Európe hral Leonardo Fibonacci. Vďaka svojim cestám a štúdiu u arabských matematikov priniesol arabský číselný systém a jeho výhody do Európy. Jeho kniha "Liber Abaci" z roku 1202 predstavila tento systém európskemu publiku a poskytla praktické príklady jeho použitia, najmä pre obchodníkov. Tým významne prispel k rozvoju matematických znalostí a obchodného sektora v Európe. Jeho práca má trvalý vplyv na matematiku a ekonómiu a je považovaný za jedného z významných matematikov stredoveku.
Záver:
Vývoj číselných systémov z primitívnych metód a nepozičných systémov k pozičným systémom s arabskými číslicami bol zásadným medzníkom pre matematiku a technológiu. Vďaka tomu môžeme ľahšie pracovať s veľkými číslami, zlomkami a vykonávať zložité matematické operácie. Leonardo Fibonacci zásadne prispel k šíreniu arabských čísel v Európe, čo malo dlhodobý vplyv na matematiku a obchodný sektor. Pozičné číselné systémy sú základom modernej matematiky a technológie, ktoré nám umožňujú lepšie porozumieť a manipulovať s číslami na úplne novej úrovni.
Ak chcete dozvedieť viac o tejto zaujímavej histórii, môžete si pozrieť nasledujúce video, ktoré nás prevedie týmto fascinujúcim vývojom.








