Pravdepodobnosť je číslo vyjadrujúce počet prípadov určitej náhodnej udalosti voči počtu všetkých prípadov. A zároveň sa tak označuje podoblasť matematiky, ktorá sa zaoberá náhodnými javmi a ich pravdepodobnosťou. Bežný človek sa stretáva s pravdepodobnosťou často, pretože svet okolo je nepredvídateľný a javí sa tak ako náhodný.
Napríklad, hoci je interval medzi dvomi spojmi na električkovej trati rovnaký, pravdepodobnosť, že budete čakať viac ako dĺžku tohto intervalu je niekedy celkom nezanedbateľná. Ja sám som často zažíval situácie, že kým mi prišiel autobus so 4 minútovým intervalom medzi spojmi, prišli 2 autobusy inej linky, ktoré majú mať 6 minútový interval.
Minca
V matematike máme radi modely, ktoré síce bývajú inšpirované reálnym svetom, ale sú trošku spoľahlivejšie. Tak napríklad taká minca, ktorou rozhodca hádže pred kopaním jedenástok vo finále ME vo futbale. Je to náhodný jav, ktorý matematici namodelujú tak, že označia jednu stranu ako hlavu, druhú ako znak a pravdepodobnosť každého z týchto javov určia, že je 1/2. Keďže pravdepodobnosť opakovaného aj paralelného hádzania mincí ja nezávislá, tak hodenie 3 mincí po sebe alebo vyhodenie 3 mincí naraz má rovnaké pravdepodobnosti, napríklad to, že padne aspoň raz hlava je 7/8.
Môže však nastať problém, že matematický model nepopisuje presne realitu. Ak mincu reálne vyhodíte do vzduchu, je možné, že experiment skončí iným výsledkom ako tým, že padne hlava alebo znak. Môže priletieť straka a vo vzduchu vám mincu zobrať. Okoloidúci kovboj ju môže zostreliť. Možno ste na plťke uprostred oceánu a minca vám padne do mora, nezistíte ako dopadla a či ju nezjedol nejaký osmonoh. Alebo môže padnúť na hranu. Tieto pravdepodobnosti sú skôr teoretické, trpezliví ľudia môžu hádzať mincou celé hodiny bez prestania a vždy im padne buď hlava alebo znak.
Ak mince dáte do tuby alebo rolky, tak ich môžete do vzduchu vyhodiť naraz aj 20. Hoci je pravdepodobnosť, že nepadne ani jedna hlava menšia ako 1/1 000 000, fyzika nepustí a rolka vám padne tak, že všetky mince budú na hrane.

Keď už sme pri minciach, kde je pravdepodobnosť dvoch javov 1/2, t.j. 50%, môžeme sa pozrieť trošku na hazard. Ruletu vymyslel slávny matematik a fyzik Blaise Pascal, aby skúmal pravdepodobnosť a štatistiku. Hazardné hry, vrátane štátnych lotérií sú rentabilné, pretože platí zákon veľkých čísel (presnejšie Kolmogorov zákon veľkých čísel). Preto stačí jedna bezvýznamná 0 a kasíno začne byť ziskové. Pravdepodobnosť padnutia konkrétneho čísla v rulete je 1/37, avšak výhra len 36 násobná.
Je taká teória, že pokiaľ budete stále vsádzať dvojnásobok prehratej sumy na jednu farbu (kým vám nepadne), nakoniec musíte vyhrať. Má to však háčik. Nie je nereálne (pravdepodobnosť asi 6%), že 4x padne iná farba. Pred piatym pokusom budete mať prehraté 15 násobok prvého vkladu a vklad 16 násobku vám s pravdepodobnosťou 18/37 umožní byť v zisku prvého vkladu. Ale pravdepodobnosť, že budete v strate vo výške 32 násobku je 19/37. Čiže v priemere ste v strate 15,4 násobku vkladu. Kým jeden môže v tejto situácii vyhrať, druhý prehrá a nakoniec nebude mať dosť na ďalší vklad. Pretože každé kolo je nezávislé. Preto kasíno neprehráva (navyše na jeden krát vám nedovolí vložiť príliš veľa).
Obdobne pri hádzaní s viacerými mincami sa bude pravdepodobnosť, že počet hláv či znakov je zhruba polovica blížiť k 1. Nikdy ju nedosiahne, ale tie okrajové javy budú úplne výnimočné.
Pri pokuse s 10 mincami je pravdepodobnosť, že hlava padne v rozsahu 45%-55%, len asi 24%. Ak budete hádzať 40x, tak tá pravdepodobnosť bude viac ako 57%. Pri 200 pokusoch už bude 86% a pri 800 pokusoch bude viac ako 99,5%.
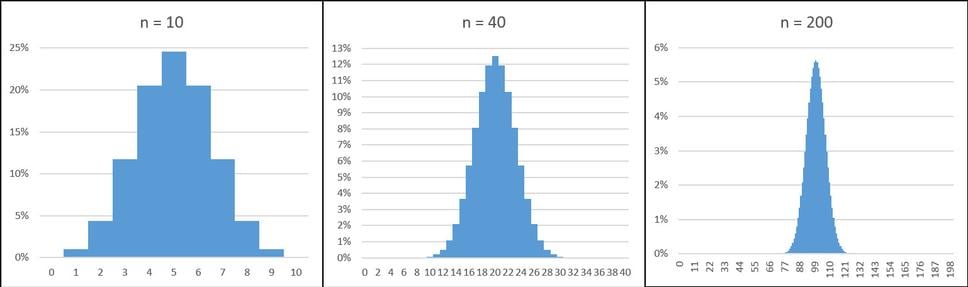
Toto je už oblasť štatistiky, ktorú používa veľká časť prírodných vied a tie humanitné odbory, ktoré nejakým spôsobom dokážu vymyslieť experiment.
Pre vnímanie náhodných čísel je osobná skúsenosť dôležitá, hoci vyjadrenie v podobe čísla (často percenta) je menej uchopiteľné. Preto zavediem kategórie, ktoré popisujú určité rozsahy pravdepodobností.
Nemožný jav má pravdepodobnosť 0 (Naopak to neplatí, ale to sa týka iba nekonečných množín).
Výnimočný jav bude pre mňa ten, ktorý má pravdepodobnosť viac ako 0 ale menej ako 0,5%. Napríklad ak sa vám podarí hodiť 8x za sebou mincu tak, že dopadne padne znak.
Zriedkavý jav je ten, ktorého pravdepodobnosť je viac ako 0,5% ale menej ako 5%. S tým sa už stretávame častejšie, je ním napríklad prvý deň v mesiaci.
Občasný jav je ten, ktorého pravdepodobnosť je viac ako 5% ale menej ako 25%.
Častý jav má pravdepodobnosť viac ako 75% ale menej ako 95%.
Zvyčajný jav má pravdepodobnosť viac ako 95% ale menej ako 99,5%.
Takmer istý je jav, ktorého pravdepodobnosť je viac ako 99,5% ale menej ako 100%.
Istý jav má pravdepodobnosť 1 (100%)
Hracie kocky
Hádzanie hracou kockou má taktiež charakter náhodného javu. Iste, keď hráte spoločenskú hru s vašim dieťaťom, je úplne časté, že ono hodí potrebnú hodnotu (obyčajne šestku) častejšie ako vy. Avšak pravdepodobnosť, že nehodíte 6 na 6 pokusov nie je taká malá. Je to viac ako 1/3. Dokonca 16 hodov po sebe bez toho, aby aspoň raz padla šestka má pravdepodobnosť viac ako 5%, čiže sa to občas stane.
Na hracích kockách si ukážeme jednu podoblasť pravdepodobnosti, ktorá sa volá podmienená pravdepodobnosť. Je to pravdepodobnosť javu A, ak zároveň nastane jav B.
Pravdepodobnosť, že nastane jav A zapisujeme P(A), pravdepodobnosť, že nastane jav B zapisujeme P(B) a podmienenú pravdepodobnosť, že nastane jav A ak nastal jav B zapisujeme P(A|B).
Hodnota P(A|B) je ako určuje definícia podiel prípadov, v ktorých nastali oba javy voči prípadom, keď nastal java B, čiže P(A|B) = P(A∩B) / P(B).
Podmienená pravdepodobnosť pri nezávislých javoch
Dva javy označujeme za nezávislé, ak P(A|B) = P(A).
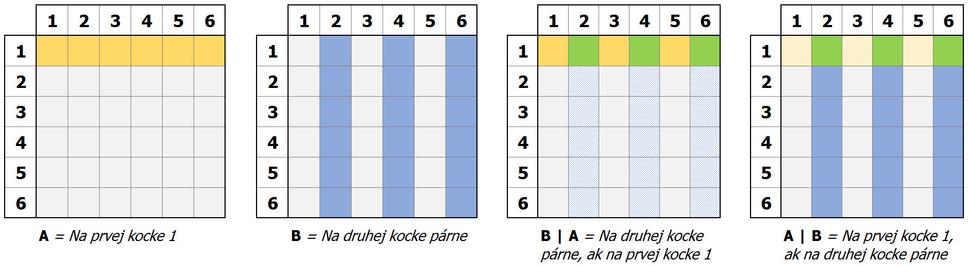
Predstavme si, že hádžeme 2 hracími kockami, ktoré vieme rozlíšiť (povedzme žltou a modrou hracou kockou). Jav A nastane, ak na žltej kocke padne 1. Jav B nastane, ak na modrej kocke padne párne číslo.
Prvý obrázok znázorňuje java A, riadky sú hodnoty žltej kocky, stĺpce hodnoty modrej kocky. Každý štvorček predstavuje kombináciu hodov na 2 kockách, jeho pravdepodobnosť je 1/36.
Potom P(A) = 6/36 = 1/6 ≈ 16,7%. Jav B nastane v 18 prípadoch z 36, takže P(B) = 18/36 = 1/2 = 50%.
Tretí obrázok predstavuje jav B (zelená), ak nastal zároveň jav A (zelená a žltá). P(B|A) = 3/6 = 1/2 = 50% = P(B).
Štvrtý obrázok predstavuje jav A (zelená), ak nastal zároveň jav B (zelená a modrá). P(A|B) = 3/18 = 1/6 = P(A).
Podmienená pravdepodobnosť pri závislých javoch
Ak ale javy nie sú nezávislé, tak rovnosť P(A|B) = P(A) nemusí platiť.
Predstavme si, že hádžeme 2 hracími kockami. Jav A nastane, ak aspoň na jednej kocke padne 1. Jav B je, že súčet hodov bude menej ako 6.
Prvé dva obrázky znázorňujú tieto pravdepodobnosti.
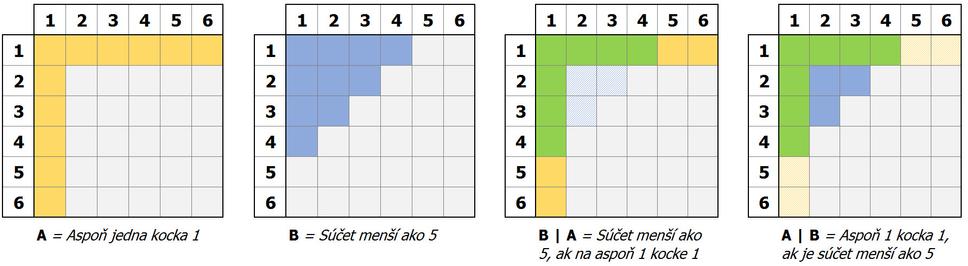
Na treťom obrázku zľava je znázornený jav P(B|A) a na štvrtom P(A|B).
Vyfarbená oblasť v P(A) predstavuje 11 štvorčekov, takže P(A) ≈ 30,6%. Vyfarbená oblasť P(B) je 10 štvorčekov, takže P(B) ≈ 27,8%.
Tieto 2 javy nie sú nezávislé, pretože P(B|A) je 7/11 ≈ 63,6%. A P(A|B) je 7/10 = 70%. Ako vidno sú to úplne iné čísla ako boli pravdepodobnosti samostatných javov A a B.
Záver
Pochopenie zložitejších javov (ako je podiel zaočkovaných v nemocniciach) je možné len ak človek chápe princípy a tie možno lepšie pochopiť na jednoduchších javoch a príkladoch. Iste do pravdepodobnosti nemožno skočiť hneď v prvej triede na základnej škole, tu je potrebné budovať základy logického myslenia a sveta matematiky.
Ako sa však ukazuje, naše školstvo ani v minulosti ani dnes nie je schopné naučiť ani logickému mysleniu a tobôž pochopeniu pravdepodobnosti nielen väčšinu obyvateľstva, ale ani bývalých elitných politických komentátorov.
Netreba však lámať palicu, matematika je krásna a pravdepodobnosť je určite zábavnejšia než počítať integrály. Na internete nájdete veľa zaujímavých a didakticky lepších článkov ako tento, len si na to treba nájsť čas a nevzdávať sa.






