Okolo Veľkej noci prišla v pracovnom zošite na rad úloha zasadená do veľkonočných vajíčok – príklady, ktoré s deťmi pracovne nazývame hrozná, pretože pripomínajú visiace strapce. Princíp je známy – do prázdnych políčok treba doplniť čísla tak, aby číslo v danom políčku bolo súčtom dvoch horných susedných políčok (neplatí pre celkom horný rad). V týchto úlohách je vašk ešte jedna podmienka - súčet doplnených čísel je daný.
V metodickej príručke autori prezradili, že druhý príklad (ružové vajíčko) má až 15 riešení. Tak veľa výsledkov je celkom zaujímavá situácia pre prvákov a snažila som sa ju využiť na vybudenie zvedavosti, čo bolo v súlade aj s mojím nastavením – sama som bola zvedavá, ako sa rôzne riešenia budú „správať. Pre takéto prípady si úlohy ani vopred nieriešim, aby som mohla objavovať spolu s deťmi.
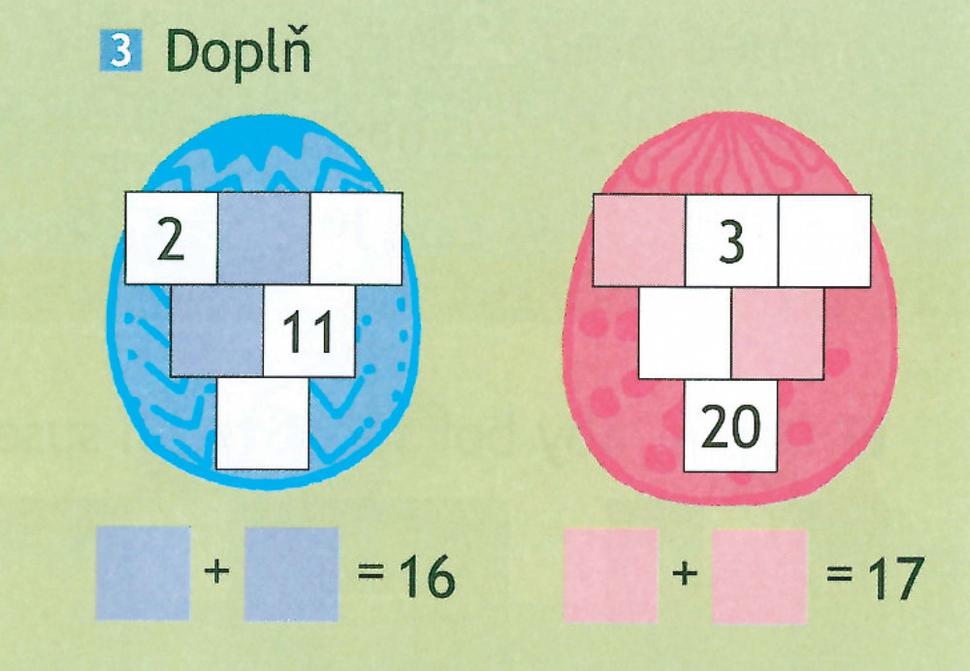
Dve úlohy v pracovnom zošite, s ktorými sme sa zabávali celú vyučovaciu hodinu (a ešte dlhšie).
Hejný,M.,Jirotková,D.,Slezáková-Kratochvílová,J.: Matematika, 2. diel, učebnica pre 1. ročník základnej školy- Premýšľanie a počítanie; Fraus 2007; Indícia 2017, ilustrovala D. Raunerová
Hroznové úlohy som premietla cez dataprojektor na tabuľu, prvé hrozno som plánovala, že budú deti riešiť samostatne a potom by nasledovalo spoločné hľadanie rôznych (15) riešení v druhom vajíčku. Ale odkiaľsi zaznela otázka: A prvá úloha má koľko riešení?
Otázky, ktoré spochybňujú očakávania považujem za veľmi užitočné a tak som sa hneď chytila príležitosti: otázku som otočila do pléna. Deti najprv odhadovali, či úloha bude mať jedno alebo viac riešení. Potom skúšali navrhovať výsledky. Niekto prvý postupoval tak, že povedal sčítance, ktoré dávali súčet 16 (8 + 8), tie sa však nedali doplniť do hrozna. Potom deti navrhovali ďalšie kombinácie, ktoré v súčte dávajú 16, ale v hrozne fungovala až posledná dvojica (7 + 9). Teda urobili sme 7 nesprávnych výsledkov/7 pokusov/7 omylov, kým sme dospeli k správnemu riešeniu.

Druhé vajíčko riešili deti samostatne. Ten, kto vymyslel nejaké iné riešenie, mohol ho zapísať na predtlačený papier, pripnutý na tabuli. Úlohu sme mali riešiť dovtedy, kým každé dieťa nemalo v svojom pracovnom zošite aspoň jedno riešenie.

Niektoré deti začali spontánne spolupracovať, hľadali ďalšie riešenia. Napokon sme ich objavili štyri.

Nie všetci však zdieľali toto nadšenie, niektorí sa aj trochu zlostili. Tomuto žiačikovi sme opäť spočítali počet pokusov na tabuli (aby sme mu ukázali, že je OK, ak sa mu nedarí hneď prvé riešenie).

Deti chceli pátrať ďalej a naozaj sa venovali počítaniu niekedy vo voľnom čase, v utorok sa na tabuli objavili ďalšie riešenia.

A keď papieriky odvial prievan, ktorési dieťa prepísalo úlohu na tabuľu – pre prípad, že by ešte niekomu napadlo iné riešenie.

Dozvuky hodiny matematiky, založenej na dvoch zdanlivo jednoduchých úlohách, trvali presne týždeň.
Deti získali skúsenosti dôležité nielen pre matematiku, ale aj pre ich ďalší osobnostný vývin:
- odhad je nie vždy v zhode so skutočnosťou – a nič sa nedeje, aj keď nie je „správny“,
- niekedy spravíme veľa pokusov (chýb), kým sa dopátrame k riešeniu,
- naše výsledky môžu byť nesprávne, ale postupne nás privedú k správnemu riešeniu (učenie sa prostredníctvom chýb),
- je zábavné skúšať nové riešenia a je zábavné skúšať počítať so spolužiakmi.
V prvých troch prípadoch sú skúsenosti priamo zacielené (aj) na dysfunkčný perfekcionizmus, ktorý je často súčasťou osobnosti nadaných jedincov. Ide o jedno z najzávažnejších rizík vo vývine osobnosti nadaných detí.
Jana Jurášková






