Pokúsim sa na jednoduchom príklade vysvetliť pojmy integrál a derivácia tak, aby ste si to vedeli predstaviť a zapamätali si to. Integrálny počet je jeden z najúžasnejších a najužitočnejších analytických nástrojov, ktorý má nezastupiteľné využitie v aplikovanej matematike v oblastiach ako fyzika, stavebné inžinierstvo, poistná štatistika, poistná a finančná matematika a neviem kde všade, ale asi všade.
V diskrétnom priestore používame funkciu suma. Ide o súčet hodnôt, napríklad suma denného zárobku nám dáva mesačný zárobok. Počítame po dňoch, teda vieme, že musíme sčítať 20 čísel. Táto funkcia v spojitom priestore nie je použiteľná, pretože by sme museli sčítať nekonečné množstvo čísiel. To je úlohou integrálu.
Predstavme si auto, ktoré ide rýchlosťou 10 m/s.
Chceme vedieť, koľko metrov prešlo auto za prvých 10 sekúnd. Vypočítame to ako súčet vzdialeností, po jednotlivých sekundách: 10+10+10+10+10+10+10+10+10+10 = 100. Je to jednoduché. Koľko prešlo auto za 100 sekúnd? To bude 1.000 x 10 = 10.000. Aj to je ľahké.
Ale čo ak rýchlosť nie je konštantná? Mení sa v čase. Najprv stúpa, potom je konštantná, nakoniec klesá až na nulu. Nemení sa len raz za sekundu, ale kedykoľvek. A cesta trvá niekoľko hodín. Spočítavať vzdialenosti po jednotlivých sekundách je dosť pracné, a ani nie presné. Pretože hovoríme o spojitých funkciách, mali by sme časové úseky deliť až na nekonečne malé úseky. Za každý tento úsek spočítať prejdenú vzdialenosť. To sa už nedá, lebo týchto úsekov je nekonečne veľa. To je spojitý priestor.
A práve na toto je dobrý integrál, môžeme si ho predstaviť ako súčet prejdených vzdialeností za nekonečne malé časové úseky. Súčet tých zvislých úsečiek na grafe 1, ale predstavte si ich nekonečne tenké a tak husto pri sebe, ako sa len dá. To nám vlastne vyplní celú plochu pod krivkou.
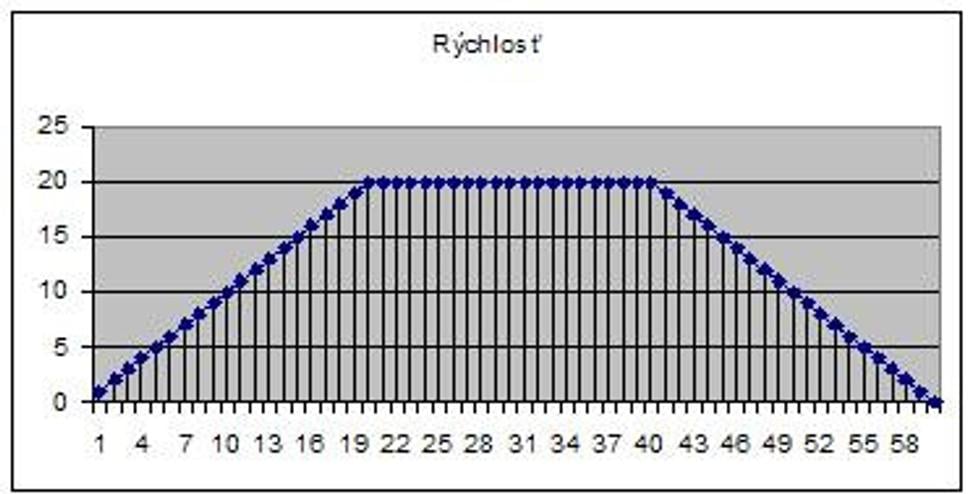
Graf 1
Takže integrál je vlastne plocha medzi krivkou (funkciou) a osou x. Obsah tejto plochy na grafe 1 je 800, to znamená, že auto prejde celkovo 800 metrov. Koľko prešlo za 40 sekúnd? Je to obsah plochy od nula do 40, čo je 600. Koľko prešlo auto od 20-tej do 40-tej sekundy? Je to obsah plochy od 20 do 40, čo je 400. Skúste si spočítať obsah tejto plochy ako obsahy dvoch trojuholníkov a jedného obdĺžnika.
Vidíme, že pre každý čas t vieme určiť práve jedno číslo ako celkovú prejdenú vzdialenosť od 0 do t. Túto funkciu sme zobrazili na grafe 2. Pozrime aké hodnoty nadobúda pre čas 60 a 40 sekúnd? 800 a 600. Ako určíme vzdialenosť medzi 20-tou a 40-tou sekundou? Ako rozdiel hodnôt pre 40-tu sekundu a 20-tu sekundu, teda 600-200=400.
Funkcia na grafe 2 je integrálom pre funkciu na grafe 1.
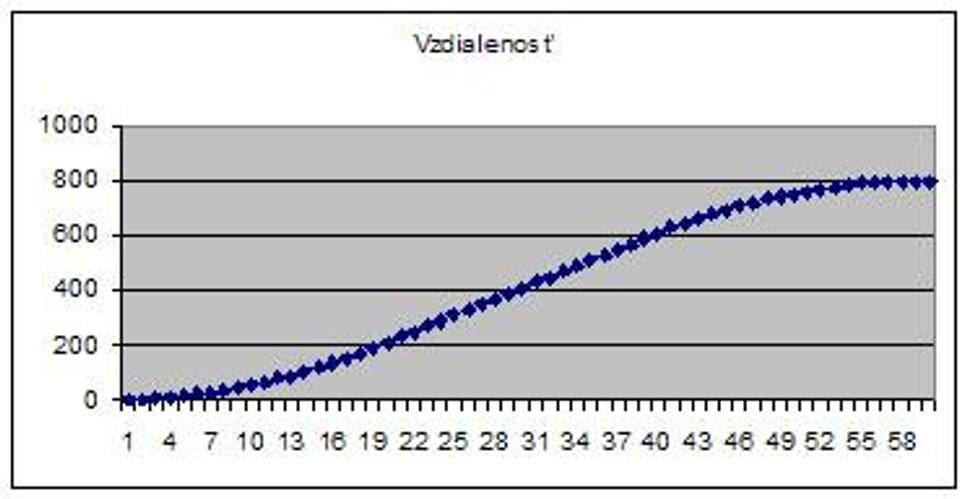
Graf 2
Teraz to popíšem vzorcami, je to trochu zjednodušený zápis, aby bol čo najzrozumiteľnejší, takže po formálnej stránke nie je dokonalý:

Použili sme vzorčeky, ktoré ste sa určite učili, ale neviete prečo sú také aké sú, proste je to tak. Ani mne učitelia nevysvetlili, prečo sú také, jednoducho sa ich treba naučiť naspamäť. Pokúsim sa vysvetliť ich logiku. Ako sme spomenuli vyjadrujú obsah plochy medzi krivkou a osou x. Naša plocha na grafe 1 sa dá rozdeliť na 3 časti:
1. trojuholník (pre x od 0 do 20). Jeho obsah je (x.y)/2 a keďže x=y, tak x.x/2
2. obdĺžnik (pre x od 20 do 40). Jeho obsah je 20x.
3. trojuholník (pre x od 40 do 60). Jeho obsah je taký istý ako 1., ale je napísaný v inom tvare, pretože funkcia klesá.
Tieto vzorce pre obsah a tvary funkcií po integrovaní sú už na prvý pohľad rovnaké. Takže vieme, že integrál funkcie je obsah plochy pod funkciou a toto pravidlo je použité aj pri tvorbe vzorcov pre integrály.
Integrál v spojitom priestore je analógiou sumy v diskrétnom priestore.
Derivácie ja vlastne opačný postup integrácie, takže na grafe 1 je derivácia funkcie z grafu 2. Derivácia je vlastne rozdiel medzi najbližšími hodnotami, graficky je to smernica krivky v danom bode na grafe 2 a na grafe 1 je to hodnota v danom bode.
Logicky, aký je rozdiel medzi vzdialenosťou prejdenou v čase t a čase t+d, ak d je blízke nule? No predsa rýchlosť v čase t. Ak d=1 sekunda, aký je rozdiel medzi vzdialenosťou prejdenou v čase t=30 a 31? Je to 20, lebo rýchlosť auta v tom čase bola 20 m/sec.
Derivácia je zmena, preto derivácia vzdialenosti je rýchlosť, derivácia rýchlosti je zrýchlenie (graf 3), derivácia zrýchlenia je zmena zrýchlenia v tom zmysle, že ak sa zrýchlenie zväčšuje, jeho derivácia je kladná a ak sa zmenšuje, derivácia je záporná. Pretože naše zrýchlenie je lineárne a konštantné, jeho derivácia je konštantná a derivácia konštanty je nula (je to zmena medzi rovnakými hodnotami, teda nula). Teda naše zrýchlenie sa nemení (až na dva body, ale to nebudem už rozpisovať).
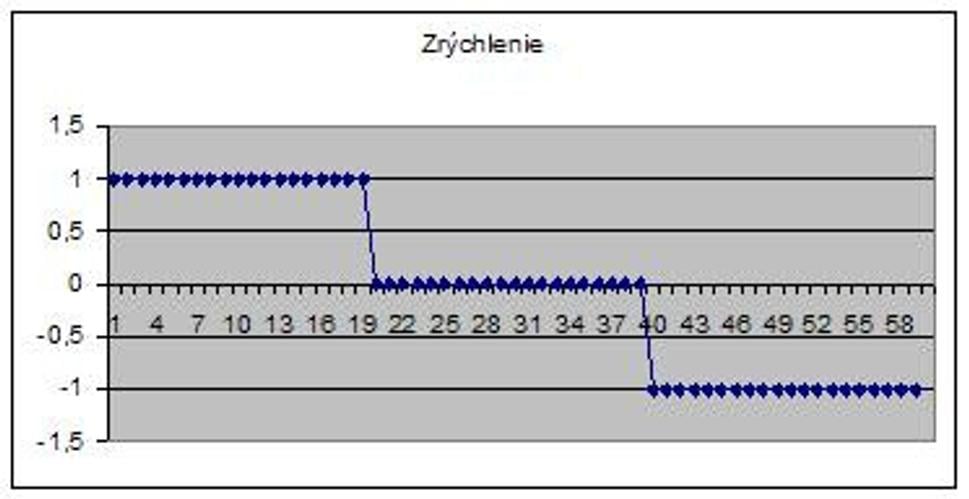
Graf 3
Derivácia v spojitom priestore je analógiou diferencie medzi susednými hodnotami v diskrétnom priestore.
Vysvetlili sme si, čo to je integrál a derivácia.
A na čo to je? Použitie je veľmi široké a ťažko sa hľadajú jednoduché príklady, ale vo všeobecnosti platí, že ak poznáme funkciu (ak poznáme priebeh okamžitej rýchlosti), dokážeme pomerne jednoducho vyjadriť jej vplyv, dôsledok, stredné hodnoty a pod (prejdenú vzdialenosť, priemernú rýchlosť, ...).
Stačí zistiť priebeh nejakej veličiny, pokúsiť sa ho čo najpresnejšie namodelovať vhodnou funkciou a môžeme aplikovať integrálny počet, podobne ako v našom príklade.
Ďalej už len pre tých, ktorí ešte vnímajú:
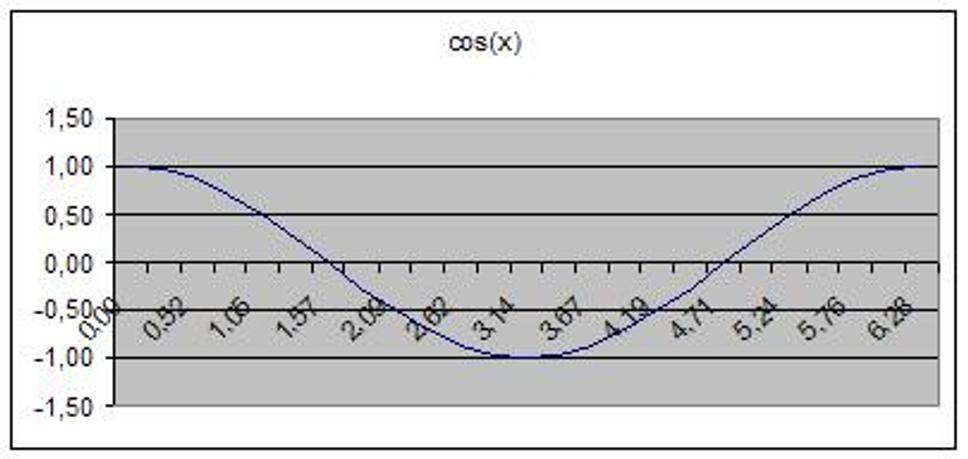
Graf 4
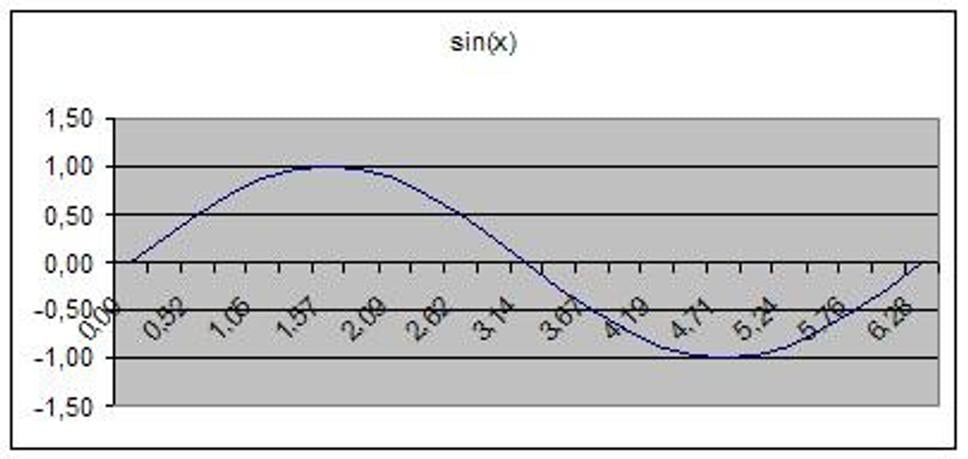
Graf 5
Pre úplnosť ešte ukážem jeden typický príklad. Integrál cos(x) je sin(x). Zobrazené sú na grafe 4 a 5. Čo môžeme z týchto grafov vyčítať:
- kým je funkcia kladná, jej integrál rastie, ak je záporná, klesá, ak je funkcia nulová, jej integrál sa nemení. Teda obsah plochy nad osou x a obsah plochy pod osou x sa navzájom odčítavajú. Preto
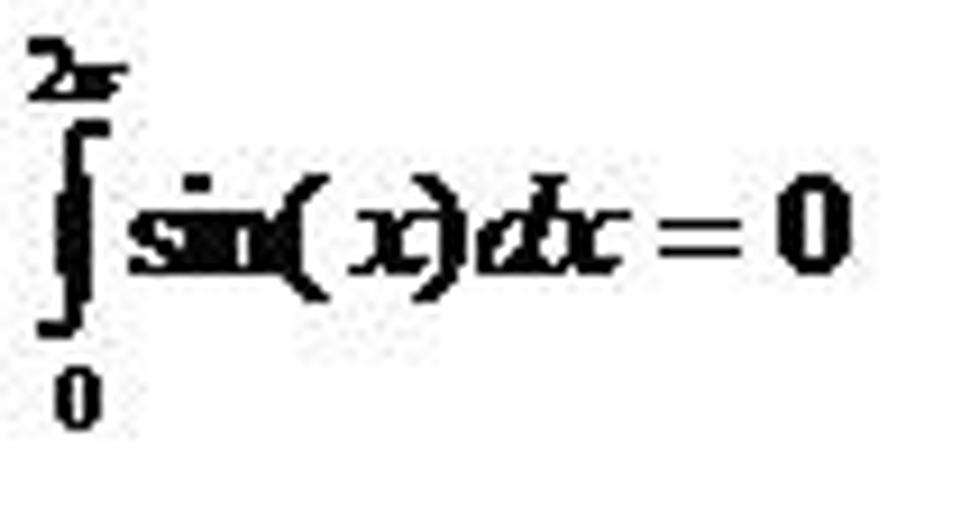
- ak funkcia klesá, jej integrál je konkávna funkcia (zatáča sa doprava). Platí od 0 do 3,14 a naopak, keď funkcia rastie, vtedy je jej integrál konvexný (zatáča sa doľava), platí od 3,14 do 6,28.
Teraz naopak si vezmime za funkciu sin(x) a jej deriváciu cos(x). Vidíme, že:
- ak je funkcia konkávna, jej derivácia klesá. Je to logické, konkávnu funkciu si môžeme prestaviť ako kopec (je to sin(x) od nula do 3,14). Jej deriváciu si predstavíme ako smernicu, alebo stúpavosť. Vidíme, že kopec je najprv strmý (derivácia =1), postupne čoraz menej strmý až po vrchol, kde je strmosť nulová (derivácia =0) a potom je strmosť záporná (až po -1). Tieto hodnoty sú deriváciou funkcie sin(x) a sú to hodnoty cos(x).
- kým funkcia rastie, derivácia je kladná (kladný rozdiel susedných hodnôt) a naopak.
Je ešte mnoho zákonitostí, ktoré platia pre funkcie, jej integrál a deriváciu. Upozornil som len na tie základné a najľahšie predstaviteľné. Ak by niekoho zaujímalo viac, môžeme v diskusii.






