(Pred pár dňami som zahliadol na inom blogu diskusiu o priemeroch a iných stredných hodnotách, nedalo mi a zareagoval som. Keďže moja reakcia bola pomerne dlhá, rozhodol som sa ju použiť ako základ článku a dať ju aj sem.)
Priemerov poznáme viac druhov, aritmetický, geometrický, harmonický, .... Pretože vyjadrujú v podstate to isté a hlavný rozdiel je v spôsobe ich výpočtu, ja budem pre zjednodušenie používať len ten najjednoduchší a najčastejšie používaný, aritmetický priemer.
Lepšie ako celé strany teórie je podľa mňa jeden dobrý príklad. Na ňom si ukážeme všetko podstatné:
Pre vyjadrenie strednej hodnoty platu v hospodárstve alebo v jeho časti, sektore, sa najčastejšie používa priemer. Preto sa to aj vola priemerná mzda. Ide o aritmeticky priemer. Ako všetci vieme, keď vám napríklad povedia, že priemerný plat vo vašej firme je 43.000 Sk, prídete na to, že väčšina z vás zarába menej. Aký je to potom ukazovateľ ten priemer?
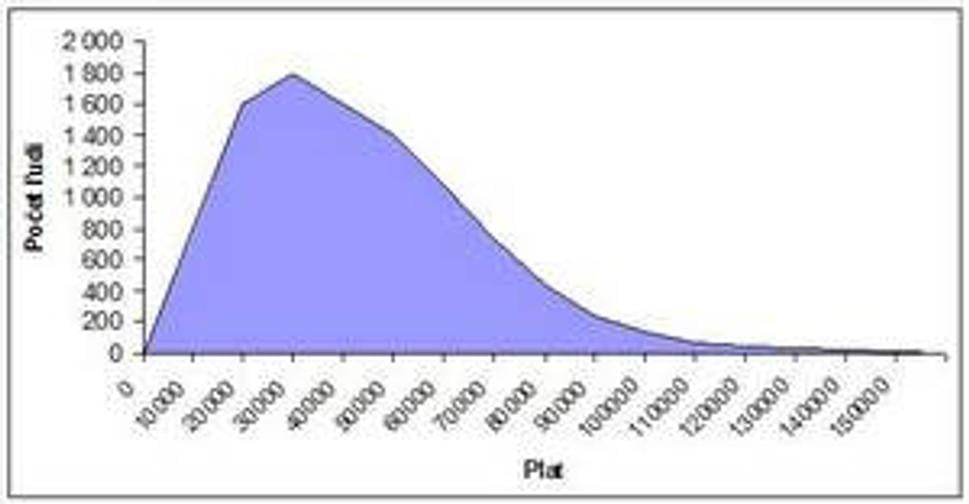
Aritmeticky priemer je veličina veľmi citlivá na extrémne hodnoty. Keďže väčšie extrémy sú doprava ako doľava (doľava sa dá ísť len po minimálnu mzdu, ale doprava do státisícov až miliónov), je jasné, že hustota pravdepodobnosti bude pravostranne zošikmená, teda, že priemer bude extrémami ťahaný doprava, k vyšším platom. Túto krivku som zobrazil na obrázku. Na osi x je plat od 0 do nekonečna. Hodnota y predstavuje počet ľudí, ktorí zarábajú plat x (pravdepodobnosti som vynásobil celkovým počtom zamestnancov 11.000, takže graf neukazuje pravdepodobnosti, ale početnosť). Jej priebeh je najprv nula a od minimálnej mzdy prudko rastie, po čase začne klesať, ale pomalšie ako rástol. Predstavte si priemer ako ťažisko tejto funkcie, lepšie povedané plochy, ktorú zviera s osou x (modrá plocha). Teda ak by ste si vystrihli túto plochu, dajme tomu z plechu, skúste nájsť bod na osi x, ktorým keď plech položíte na svoj prst, bude v rovnováhe. A práve tento bod je aritmeticky priemer. V našom príklade 43.000 Sk.
Ak držíte balans na lane a máte v rukách tyč, motýľ, ktorý si sadne na jej koniec môže vaše úsilie o rovnováhu narušiť viac ako kilové závažie hneď vedľa vašej ruky. A takto sa správa aj naše ťažisko - aritmeticky priemer. Jeden človek, ktorý zarába extrémne veľa má na priemer najväčší vplyv. Dokonca to, že či najlepšie zarábajúci manažér vo finančníctve zarába 2 mil. alebo 3. milióny, má veľký vplyv na veličinu, ktorou merajú ekonomicky blahobyt všetkých zamestnancov firmy. A práve táto citlivosť na extrémne hodnoty je jednou z najväčších slabín aritmetického priemeru.
(Iný príklad: Firma má 2 zamestnancov s platom 20.000 Sk a šéfa s platom 110.000 Sk. Priemerný plat je 50.000. To neznamená, že ak nastúpi nový zamestnanec s platom 40.000, bude nespokojný, že zarába podpriemerne.)
Ako sme si povedali, v tomto príklade sú extrémne hodnoty viac vpravo, inak povedané hustota pravdepodobnosti je pravostranne zošikmená funkcia, čo znamená že aritmetický priemer (náš prst rovnováhy) musí byt posunutý vpravo.
To má za následok, že iné dve najbežnejšie veličiny používané na určenie strednej hodnoty, medián a modus, sú vľavo od priemeru. Ani jedna z nich nie je citlivá na extrémne hodnoty, to znamená že budú viac v strede.
Modus ja najčastejšie sa vyskytujúca hodnota, preto je vhodná na meranie strednej hodnoty mzdy. Určuje výšku mzdy, ktorú zarába najviac ľudí, čiže určuje akúsi ľudovú mzdu, najviac rozšírenú. Je to zrejme mzda úradníkov juniorov, tých je najviac. Na našom grafe je to maximum funkcie hustoty pravdepodobnosti, na našom plechu je to miesto, kde je plech najvyšší. Je to hodnota 30.000 Sk. Výhodou tejto strednej hodnoty je v jej jednoduchej interpretácii a je ľahko predstaviteľná.
Medián delí celé spektrum na polovicu. Určuje takú výšku platu, že polovica ľudí zarába menej a polovica viac ako tento plat. Na našom plechu je to ta hodnota na osi x, kde keď plech rozrežeme na dve časti smerom kolmo hore, rozdelí sa nám na dve časti s rovnakým obsahom. To je polovica ako vyšitá, že? Je to hodnota 40.000 Sk. Je napravo od modusu, ale naľavo od priemeru, teda opäť v strede. Prečo je napravo od modusu? Pretože modus v tomto prípade delí náš plech na dve nerovnaké plochy a menšia je ta vľavo, čo je opäť spôsobené pravostranným zošikmením.
Z toho čo som napísal možno mate dojem, že priemer je najhoršia zo stredných hodnôt a mali by sme ju zo života eliminovať, keďže je taká zavádzajúca. Bohužiaľ nie je to tak, priemer má jednu obrovskú výhodu. Ako jediná z uvedených hodnôt obsahuje v sebe maximum informácie o súbore a preto je najvhodnejšia na matematické a štatistické výpočty. (Ak poznáme priemer a počet zamestnancov, poznáme aj celkovú mzdu, o mediáne a moduse sa to povedať nedá). A viete prečo, lebo je v nej zaznamenaná každá informácia, informácia o každej hodnote aj o jej vplyve na cely súbor, to znamená aj o informácii o každej extrémnej hodnote, dokonca aj o jej váhe, sile. Aj preto, že je maximálne citlivá na extrémne hodnoty, pretože extrémne hodnoty majú najväčší vplyv na celý súbor. A sme znova na začiatku, najväčšia nevýhoda priemeru je vlastne jeho najväčšou výhodou.
Takže ako sa správne pozerať na to, aký máme plat? Priemer nám veľa nepovie, je skreslený extrémnymi hodnotami – šéfovskými platmi. Modus hovorí, koľko zarábajú bežní zamestnanci, môžeme povedať „priemerne“. Ak mám menej, treba pridať. Ak zarábam viac ako je modus, zaujímavé by bolo poznať medián. Ak zarábam viac ako je medián, patrím do lepšie zarábajúcej polovice zamestnancov. Preto, myslím, medián má v tomto prípade najlepšiu vypovedajúcu schopnosť.
Z obrázku vidíme, že naše 3 stredné hodnoty nám rozdeľujú celé spektrum na 4 intervaly. Pokúsim sa o interpretáciu platu podľa toho, do ktorého intervalu patrí:
(0 ; modus) – plat je menší ako plat, ktorý poberá najviac ľudí vo firme. Mali by ste pridať. Zarábate menej ako referent junior, alebo robotník v stavebnej firme. Pri troche nadhľadu môžeme povedať, že zarábate menej ako zarábajú “priemerne“ bežní zamestnanci.
(modus ; medián) – máte slušný plat v tom zmysle, že síce patríte do menej zarábajúcej polovice, ale na druhej strane máte viac ako je „ľudový plat“, čiže viac ako referent junior/robotník.
(medián ; priemer) – je pravdou, že stále zarábate „podpriemerne“, ale to nech vás netrápi. Dôležité pre vás je, že zarábate viac ako polovica ľudí vo firme. O tom priemere sme už hovorili. Zrejme už nie ste radový zamestnanec.
(priemer ; ∞) – máte výborný plat, je nadpriemerný, pravdepodobne ste na úrovni najmenej nižšieho managementu.
Ako vidíte, tie vyššie, šéfovské platy sú všetky v jednom intervale, v tom poslednom. Znamená to, že tie už nedelíme? Nie, celé spektrum sa dá deliť na nekonečné množstvo intervalov. Najznámejšie sú percentily, ktoré nám ho delia na 100 intervalov, niečo ako medián, ktorý nám spektrum delí 50:50, čo je vlastne 50. percentil. Ale o tom možno až nabudúce.
(Poznámka:
Uvedené rozloženie stredných hodnôt platí pre pravostranne zošikmené krivky, teda také, kde je viac hodnôt v ľavej strane spektra, vpravo je menej hodnôt, ale vzdialenejších od stredu. Pri symetrickom rozdelení (ktoré nie je zošikmené), napríklad normálne rozdelenie, sa priemer, medián a modus rovnajú.
Použil som niekoľko zjednodušení, aby bola princíp ľahšie predstaviteľný, napríklad platy som rozdelil do niekoľkých skupín po 10.000 Sk a početnosti vyjadrujú počet platov v dajnej skupine, teda zo spojitej funkcie sme prešli na diskrétne početnosti. Graf preto udáva, napr. že počet ľudí, ktorí zarábajú od 50 do 60 tisíc Sk je cca 1.200. Preto, aby sme mohli hovoriť o plechovej ploche, som graf zobrazil ako spojitú funkciu. Ale nenechajte sa tým pomýliť.
Takisto som použil menej formálny jazyk preto niektoré definície nie sú absolútne presné, ale možno ľahšie pochopiteľné. Ak bude záujem, nabudúce môžeme ísť do problematiky hlbšie.)






