Zaujímavá otázka.Položili mi ju moji kolegovia pri káve a zaujalo ma to, tak som sa pozrel natento problem zbližšia.Rozhodol som sa urobiť jednoduchý počítačový model tejto úlohy v Ecxceli. Tu je model na stiahnutie.
A tu je fyzikálna úvaha, z ktorej som pri modelovaní vychádzal.
Ako pri každom modeli nejakého reálneho problému, na začiatku si musíme stanoviť nejaké predpoklady. Východiskovézjednodušenia, ktoré som si dovolil urobiť, sú tieto tieto tri:
1. Gravitačné zrýchlenie budeme považovať zakonštantné v akejkoľvek výške nad povrchom zeme.
Totozjednodušenie nie je až taký veľký hriech, pretože gravitačné zrýchlenie sa nadpovrchom zeme mení približne o 0,003 % na 100 m výšky. Vo výške 100 km nadpovrchom Zeme je teda gravitačné zrýchlenie približne 9.5 m.s-2.V našom modeli tento úbytok môžeme zanedbať. Môžeme sa dohodnúť, žez vyšších výšok hádzať nebudeme.
2. Teplotu atmosféry považujeme konštantnúv každej výške nad zemou.
Teplotu atmosférypotrebujeme pri výpočte hustoty vzduchu v určenej nadmorskej výškea na výpočet rýchlosti zvuku. Predpoklad konštantnej teploty takistonepredstavuje až takú výraznú chybu, pretože rozdiel teplôt medzi povrchom zemea výškou 10 km nad zemou je obvykle približne 50°C, čo v našomprípade takisto nepredstavuje výrazný rozdiel pri výpočtoch.
3. Rýchlosť zvuku je konštantná v každejvýške pri zvolenej teplote prostredia.
Samozrejme, predpokladáme aj úplné bezvetrie, aby nám teleso padalo pekne rovno na zem a neunášali ho nejaké bočné vetry alebo víry.
Teleso, ktorébudeme púšťať na zem, môže mať rôzny tvar. Veľkosť odporovej sily vzduchu odtvaru telesa závisí. Tvar telesa reprezentuje tvarový koeficient – bezrozmernákonštanta, ktorá je tým menšia, čím má teleso „aerodynamickejší“ tvar.Napríklad, kužeľ s uhlom 30° pri vrchole, ktorý vzduch dobre rozráža, má odporovýkoeficient 0,34, ale napríklad štvorcová doska má tento koeficient 1,11. ChevroletCorvette má koeficient odporu 6,57. V excelovskom modeli si môžeme vybraťz ôsmich rôznych tvarov a na základe zvoleného tvaru telesa sa navýpočet odporovej sily použije príslušný koeficient a vypočíta sa príslušnápriečna plocha telesa.
Rozoberme sinajskôr prvý prípad, teda hustotu atmosféry budeme považovať za rovnakú v každejvýške nad zemou.
Na začiatkufyzikálneho rozboru pohybu telesa si musíme uvedomiť, aké sily pôsobia na našeteleso. V smere nadol ho k sebe priťahuje zem svojou tiažovou silou,ktorá je daná súčinom hmotnosti telesa a gravitačného zrýchlenia:
F = m.g.
Keď telesopustíme na zem zo zvolenej výšky, zo začiatku bude padať voľným pádom, čoznamená, že sa bude pohybovať s gravitačným zrýchlením g. Proti smeru pohybu telesa pôsobíodporová sila vzduchu, ktorá teleso brzdí. Od čoho všetkého závisí veľkosť odporovej silyvzduchu? V prvom rade od rýchlosti telesa, potom od hustoty vzduchu, odtvarového koeficientu a od priečnej plochy telesa (plochy kolmej na smerletu). Postupne, ako teleso naberá rýchlosť, zväčšuje sa aj odporová sila. Matematickýzápis odporovej sily ste sa učili v prvom ročníku na strednej škole – vyzerátakto:
F = (1/2).ρ.C.S.v2.
V tomtozápise ρ predstavuje hustotu prostredia, S priečnu plochu telesa, Ctvarový odporový koeficient a v rýchlosť.
Keďže odporvzduchu teleso brzdí, po istom čase od vypustenia už nebude padať voľným pádom.Bude sa síce pohybovať stále zrýchleným pohybom, ale nie s konštantnýmzrýchlením g, ale so zrýchlením,ktoré sa s časom zmenšuje. Výsledné zrýchlenie telesa gvýs je tedačasovo premenná veličina a môžeme ju napísať ako
gvýs = g - aO ,
kde aO predstavujespomalenie (odporové zrýchlenie) telesa spôsobené odporom vzduchu. Totozrýchlenie je časovo premenné (zvykne sa to písať ako aO(t), čoznamená že a je funkcia času),pretože veľkosť spomalenia sa mení s narastajúcu odporovou silou, ktorázávisí od rýchlosti, a rýchlosť pri zrýchlenom pohybe, ako vieme,s časom narastá.
Odporová silavšak nebude narastať donekonečna. Keď sa odporová sila vzduchu vyrovná tiažovejsile F=m.g, teleso prestane zrýchľovať a bude sa ďalej pohybovaťrovnomerným priamočiarym pohybom, až kým necapne na zem.
Ako vypočítame veľkosťspomalenia – odporového zrýchlenia aO ?Použijeme Newtonovu rovnicu pre silu a odporovú silu napíšeme ako
FO = m.aO .
Za silu do tejtorovnice, prirodzene, dosadíme vzťah pre odporovú silu a dostaneme rovnicu
(1/2).ρ.C.S.v2 = m.aO .
Aby sme mohlisprávne namodelovať pohyb telesa v každej sekunde po vypustení, musímez tejto rovnice vyjadriť spomalenie a.
Na ľavej strane rovnicemáme rýchlosť. Vieme však, že rýchlosťtelesa v nejakom určitom čase závisí od jeho zrýchlenia v tomto časepodľa vzťahu
v = a.t .
Tu si však musímedať pozor, pretože uvedený vzťah platí len pre rovnomerne zrýchlený pohyb(pohyb s konštantným zrýchlením). Ak sa zrýchlenie v čase mení,rýchlosť sa musí vypočítať ako integrál z funkcie zrýchlenia. Avšak princípnumerického modelovania, ktoré ideme použiť, je ten, že časový priebehzrýchlenia „rozbijeme“ na také malé úseky, že na týchto úsekoch budeme považovaťzrýchlenie za konštantu. To znamená, že môžeme použiť vzťah v = a.t. Za zrýchlenie dotohto vzťahu dosadíme výsledné zrýchlenie telesa g výs , teda
v = gvýs.t = (g - aO).t .
Rovnica, z ktorejchceme vyjadriť odporové zrýchlenie, potom prejde do tvaru
(1/2).ρ.C.S.(g - a)2 = m.aO . Na tejto úrovnikončí fyzikálna úvaha a prichádza na rad matematika. Potrebujeme vyjadriťz rovnice a O , ktorévystupuje na ľavej strane v druhej mocnine a na pravej strane v prvejmocnine. Musíme teda vyriešiť kvadratickú rovnicu. Nebudem riešiť celú rovnicu,napíšem priamo výsledok, ktorý z nej dostaneme:
a(t) = g + (m/ρ.C.S.t2) ± √{[2g + (2m/ρ.C.S.t2)]2 - 4g2} Pretože vovýsledku je plus mínus, môžeme dostať dve riešenia (dva reálne korenekvadratickej rovnice). Fyzikálny význam má pre náš prípad tá so znamienkommínus, teda výsledný vzťah pre zrýchlenie, ktorý použijeme v modeli je
a(t) = g + (m/ρ.C.S.t2) - √{[2g + (2m/ρ.C.S.t2)]2 - 4g2}
Ostáva nám už lenpodosádzať do vzťahu všetky konštanty a môžeme vypočítať spomalenie v akomkoľvekčase t po vypustení telesa. Keď totospomalenie odčítame od gravitačného zrýchlenia, vyjde nám zrýchlenie telesa v danomčase. Zo zrýchlenia vieme pre daný čas vypočítať rýchlosť, a z rýchlostizase dráhu, ktorú teleso urazí v nami zvolenom malom časovom intervale, naktorom sa dohodneme, že budeme považovať zrýchlenie za konštantu. V excelovskommodeli som zvolil časový interval jednu sekundu.
Môžeme si tedaveselo zvoliť počiatočné podmienky a pozrieť sa, ako bude vyzerať pohybtelesa. Tak napríklad, ak vypadne človek s hmotnosťou 101 kg z výšky 10km nad zemou, zrýchlenie sa bude meniť takto:
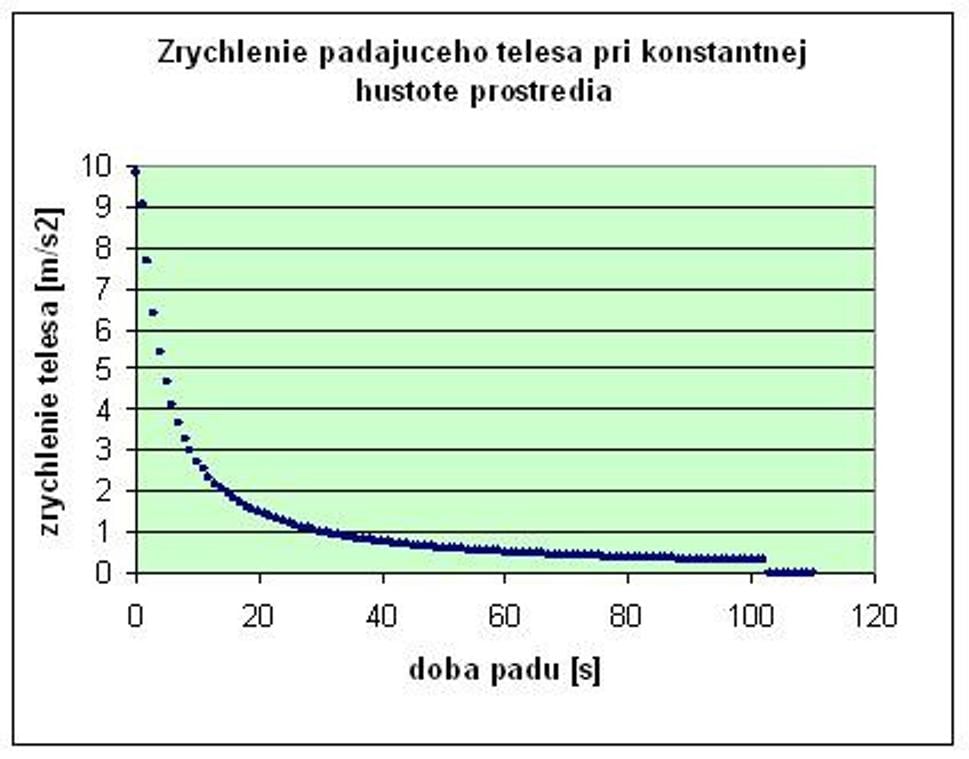
Z grafu vidíme,že zrýchlenie sa postupne zmenšuje. Po približne 80 sekundách pádu klesne takmerna nulu, čo znamená, že už skoro vôbec nezrýchľuje, ale padá približnekonštantnou rýchlosťou. Po 102. sekunde dopadne na zem s rýchlosťou asi 129m/s (okolo 465 km/h). Z nasledujúceho grafu vyčítame, že aj keď je tátorýchlosť dosť veľká (okolo 465 km/h), na prekonanie rýchlosti zvuku to zďalekanestačí.
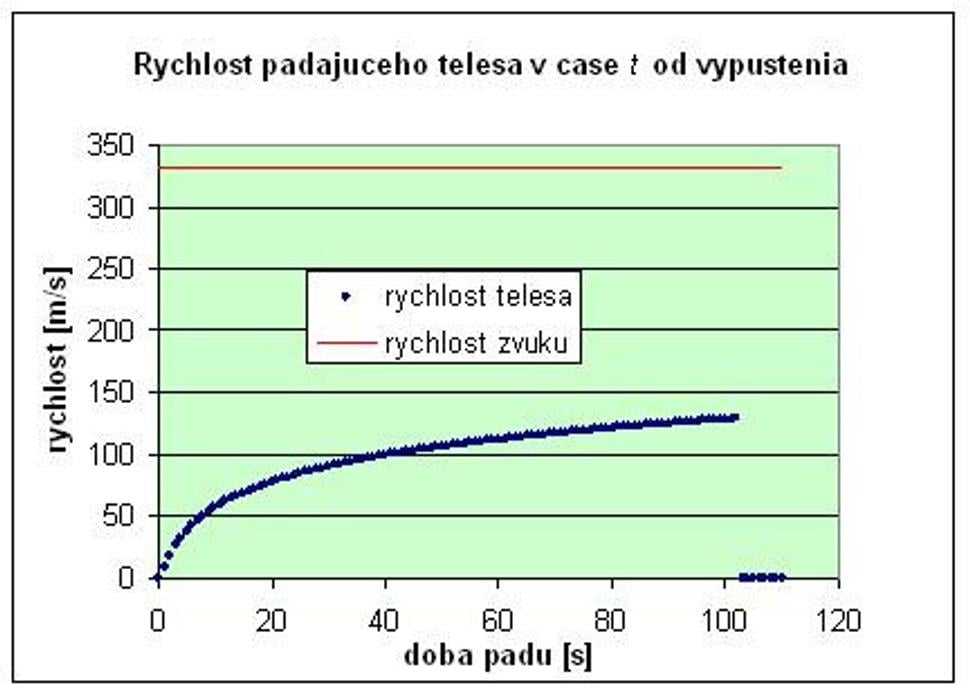
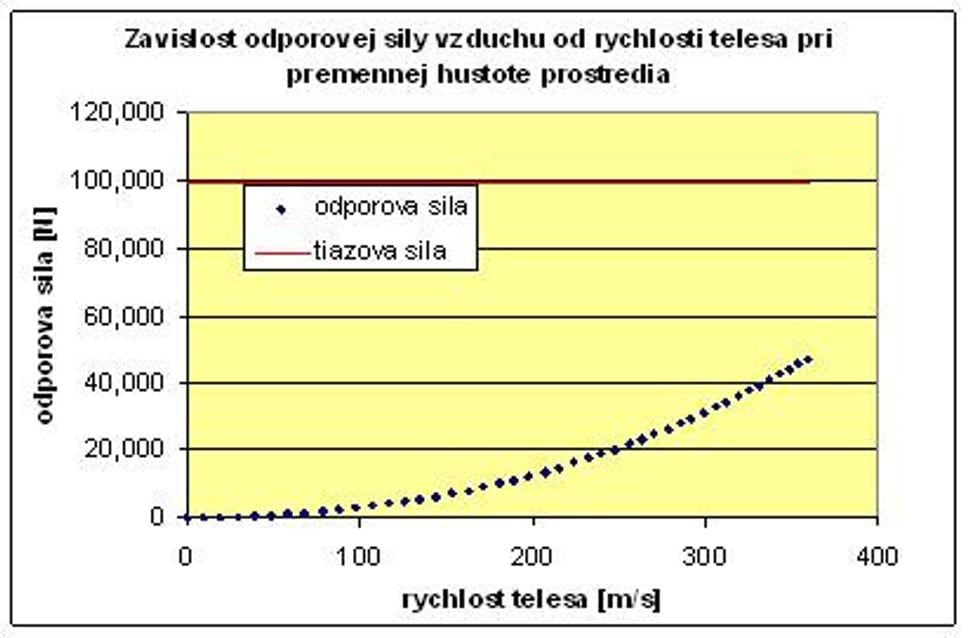
V ďalšom grafevidíme, ako narastá odporová sila vzduchu s narastajúcou rýchlosťou telesa.Pri rýchlosti okolo 120 m/s sa teda obe sily zhruba vyrovnajú, preto sa užspomalenie viac neuplatňuje.
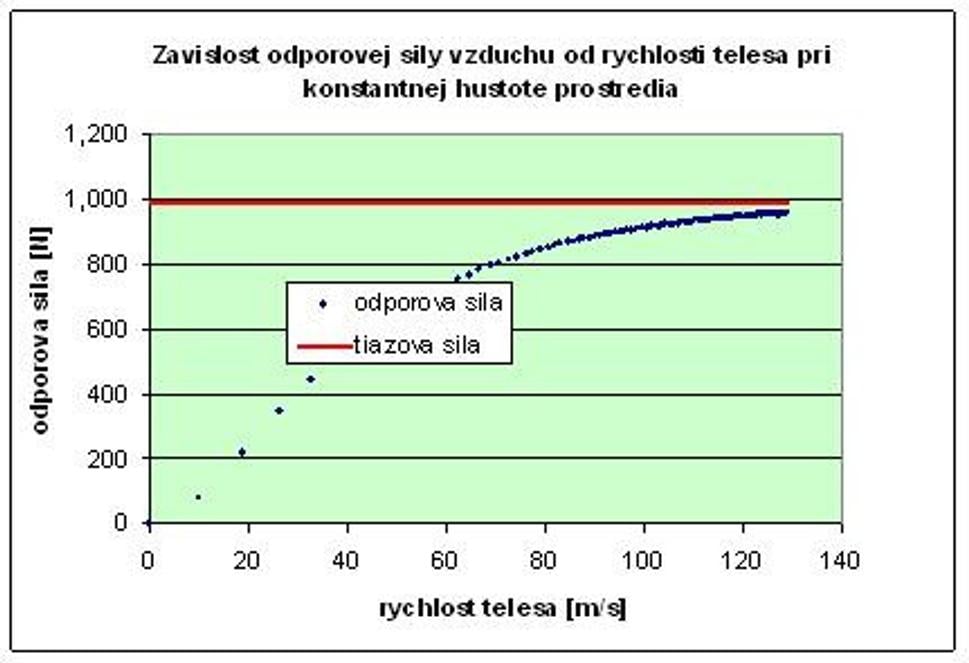
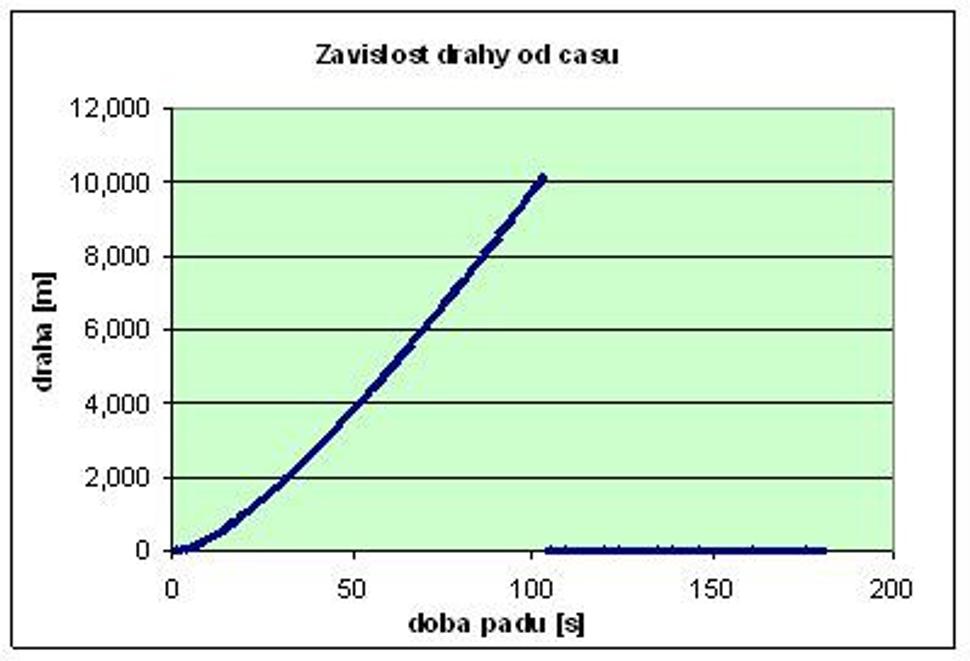
V excelovskommodeli nájdeme ešte grafy iných závislostí, napríklad rýchlosti od výšky nadzemou (môžeme na ňom vidieť, akú rýchlosť bude mať teleso pri dopade na zem),graf odporovej sily od výšky nad zemou (môžeme z neho vyčítať, ako sauplatňuje odporová sila pri istej výške nad zemou), alebo graf dráhy od času,ktorý ukazuje, ako sa mení priebeh dráhy – najskôr je priebeh kvadratický (kriváčiara), neskôr, keď zrýchlenie klesá, sa zmení na lineárny (rovná čiara).

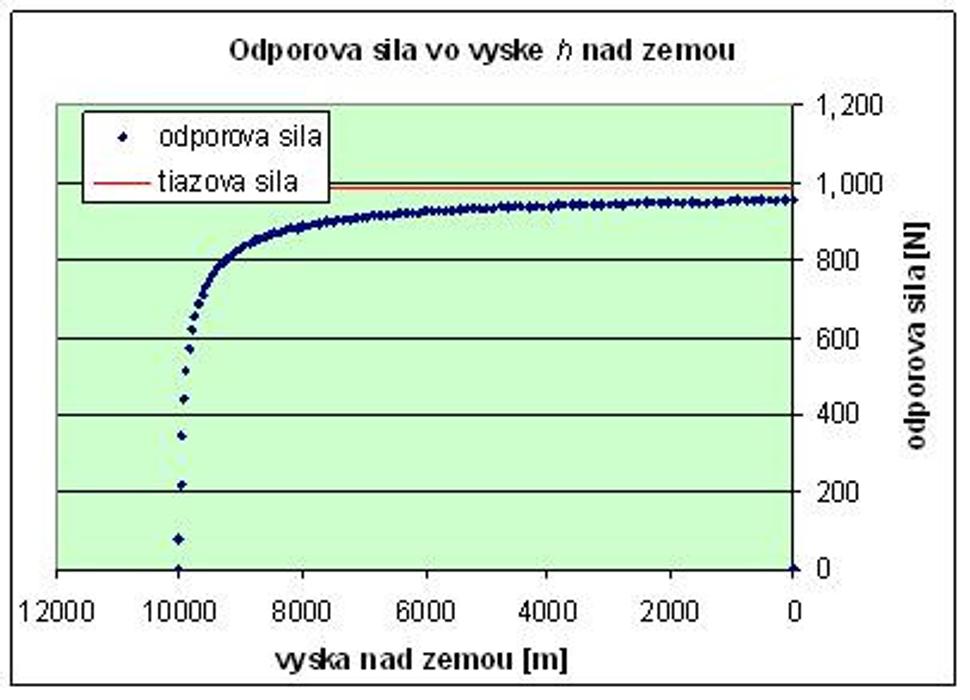
V modeli simôžeme meniť vstupné parametre, a uvidíme, pri akom telese a akej počiatočnejvýške by sme rýchlosť zvuku pri dopade dosiahli. Tak napríklad, ak by smenamiesto človeka zhodili olovenú guľu z výšky 20 km, na zem by dopadlarýchlosťou takmer 350 m/s (1257 km/h). Šupa, však? Vyskúšajte si sami rôzne inékombinácie telies, tvaru a výšky.
Dobre teda. Mámemodel pre prípad, keď je hustota atmosféry všade rovnaká (v excelovskom modelisú tieto grafy v záložke „Konštantná hustota“). Ako však dobre vieme, čímsme vo vyššej nadmorskej výške, tým je vzduch „redší“. Vzťah, podľa ktorého sahustota atmosféry mení s výškou nad zemou, našiel pán Boltzmann, preto satento vzťah volá Boltzmannov barometrický zákon a vyzerá takto: ρ(h) = ρ .exp(-mgh/kT)
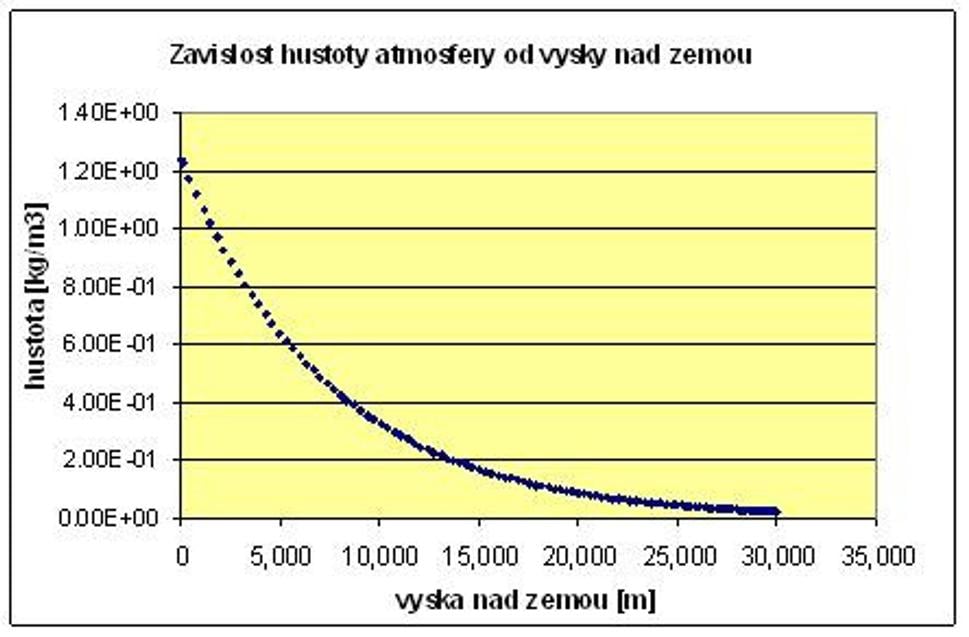
kde ρ(h) je hustota atmosféry vo výške h nad zemou, ρ0 je hustota atmosféry pri hladine mora, a veličiny v zlomku v exponente Eulerovho čísla sú m – hmotnosť jednej molekuly vzduchu, g – gravitačné zrýchlenie, h – nadmorská výška, k – Boltzmannova konštanta a T je teplota okolitej atmosféry v Kelvinoch.Keď si nakreslíme graf tejto funkcie, vidíme, že hustota klesá s nadmorskouvýškou exponenciálne (teda veľmi výrazne).
Úloha sa trochu komplikuje,pretože do vzťahu pre spomalenie a O vstupuje hustota. V prvom prípade sme ju mohli dosadiť v každejvýške nad zemou rovnakú. V tomto prípade (ktorý je bližší realite) jumusíme prepočítať nanovo pre každú výšku, v ktorej sa teleso nachádza. Akoto urobiť?
Opäť to urobímetak, že pohyb telesa „rozbijeme“ na drobné časové kúsky po jednej sekunde. Budemepritom predpokladať, že pre dráhu, ktorú teleso počas jednej sekundy prejde,môžeme považovať hustotu za konštantu. Prepočítame ju potom nanovo pre novúvýšku, v ktorej sa teleso nachádza v ďalšej sekunde.
Výsledkom súgrafy, ktoré sa v excelovskom modeli nachádzajú v záložke „Premennáhustota“. Pre prípad človeka, ktorý vypadne z výšky 10 km nad zemou budúgrafy vyzerať takto:
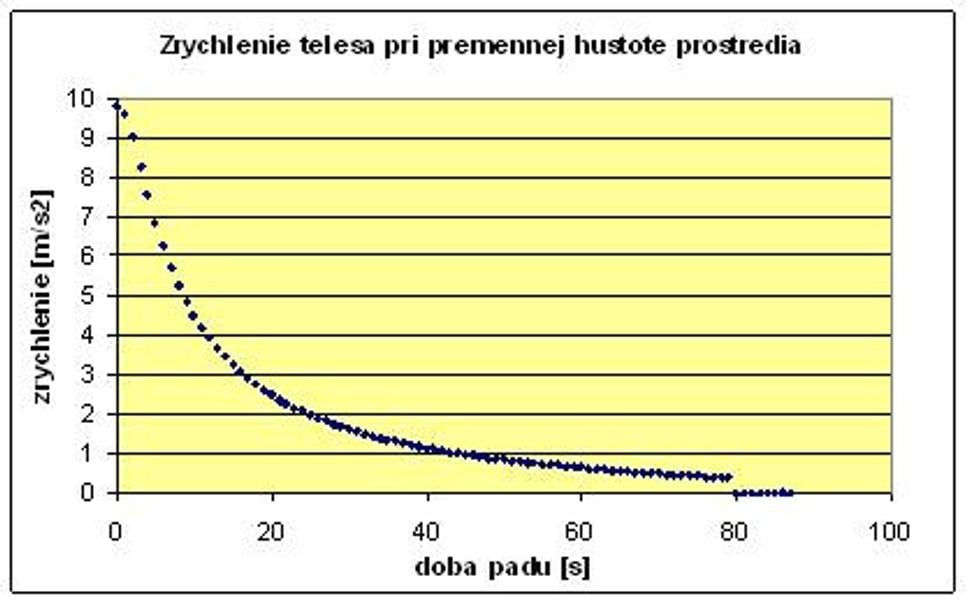
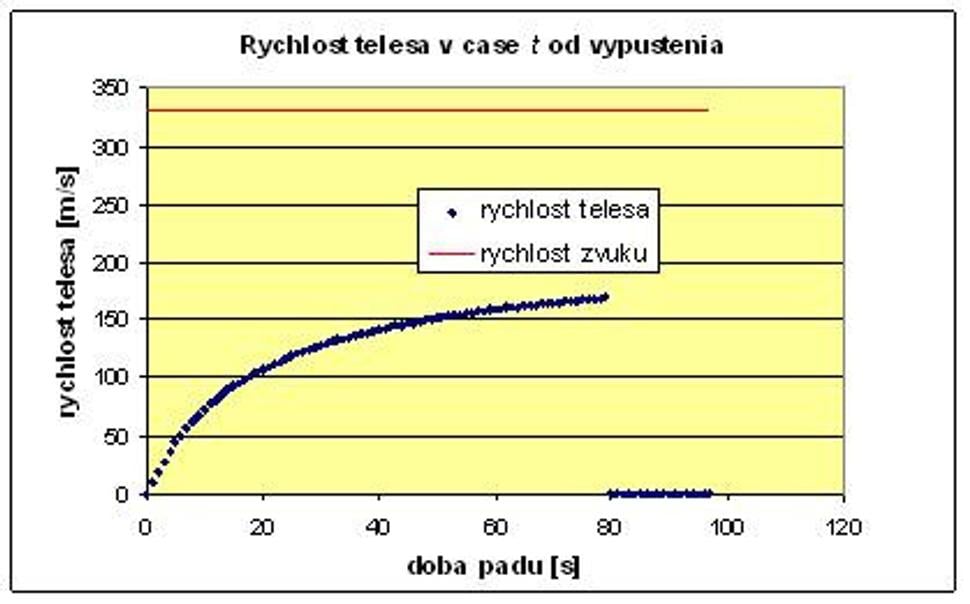
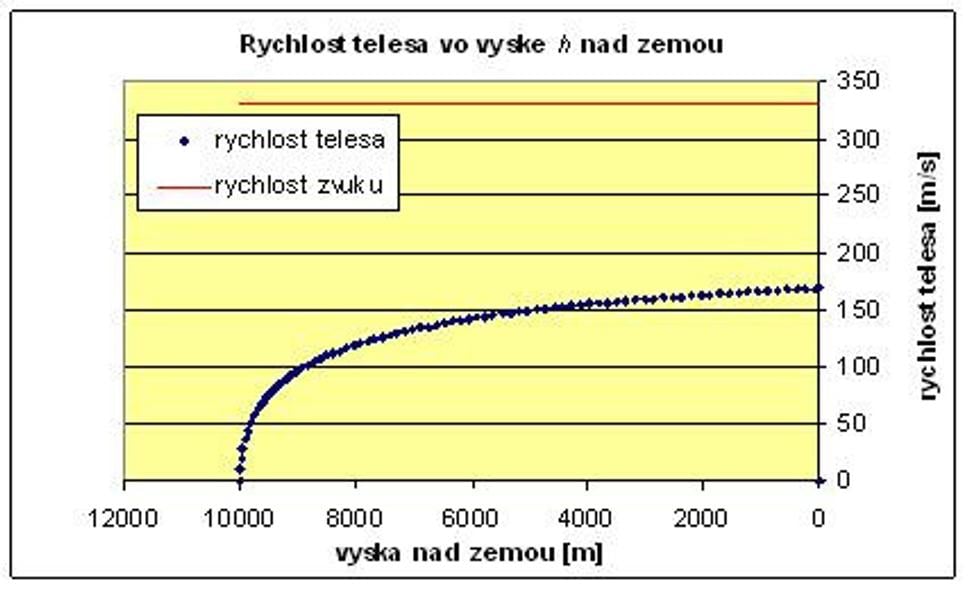
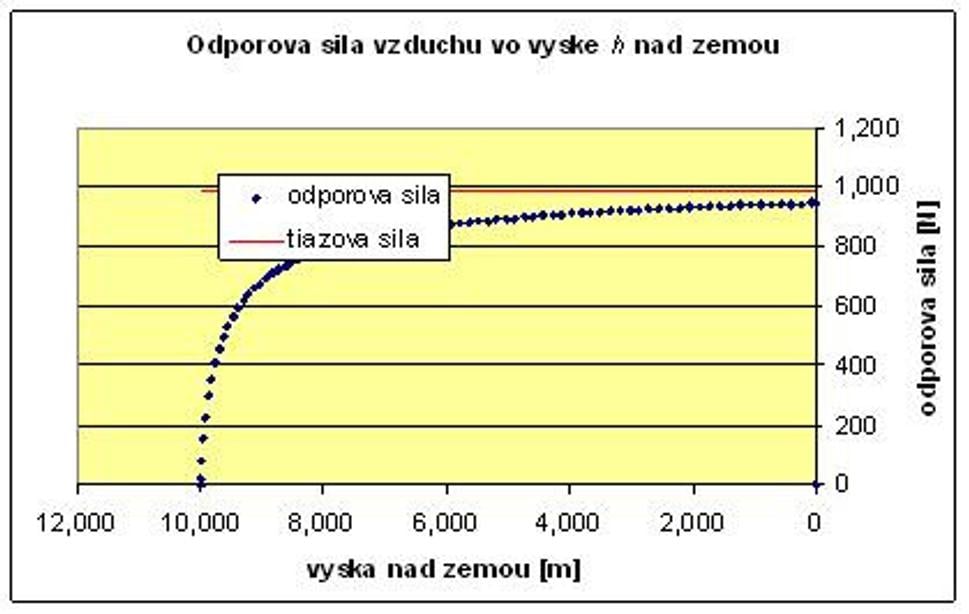
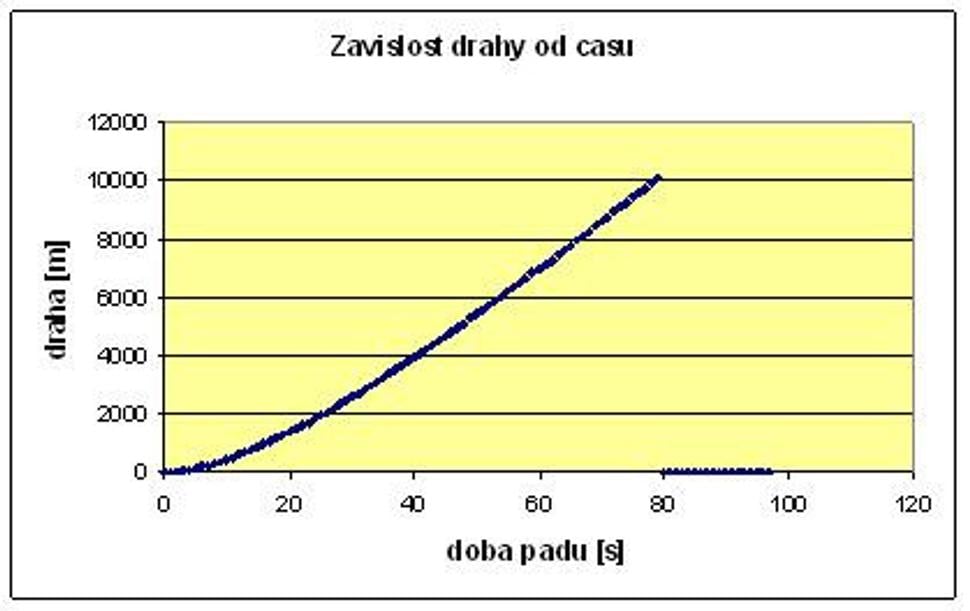
Z grafov vidíme, že teleso sa pohybuje trochudlhšie voľným pádom, pretože zrýchlenie telesa klesá pomalšie, ako v prvomprípade. Je to tým, že vo väčšej výške, kde je atmosféra redšia, sa odporvzduchu uplatňuje menej, a odporová sila narastá pomalšie.
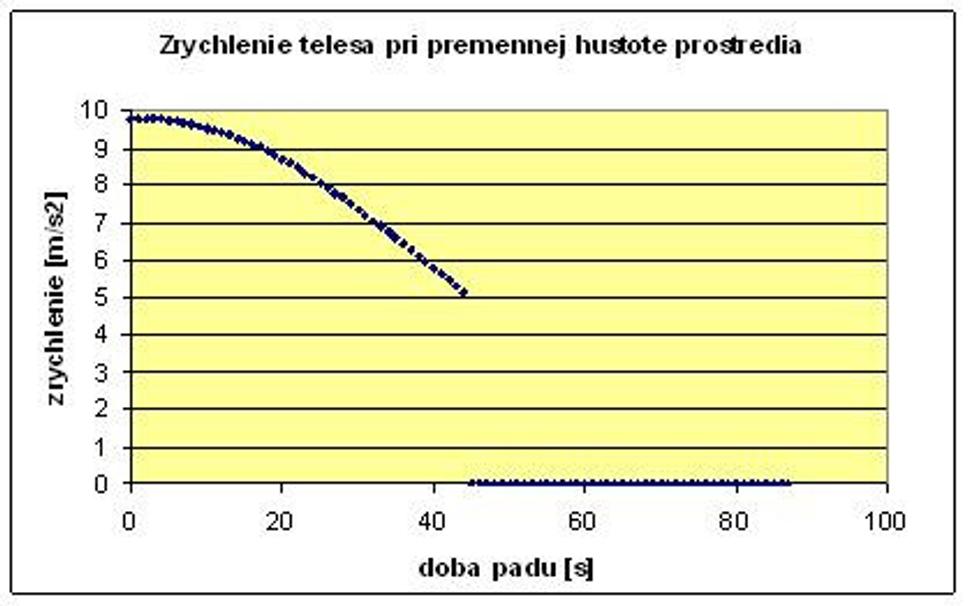
V modeli si môžete zvoliť napríklad guľu zozlata s priemerom 1m, ktorú keď zhodíme z výšky približne Mt. Everestu,tak na zem dopadne po 46 sekundách a pri dopade dosiahne rýchlosť približne 342m/s (1233 km/h), čo je rýchlosť zvuku prekonaná o 125 m/s (450 km/h).
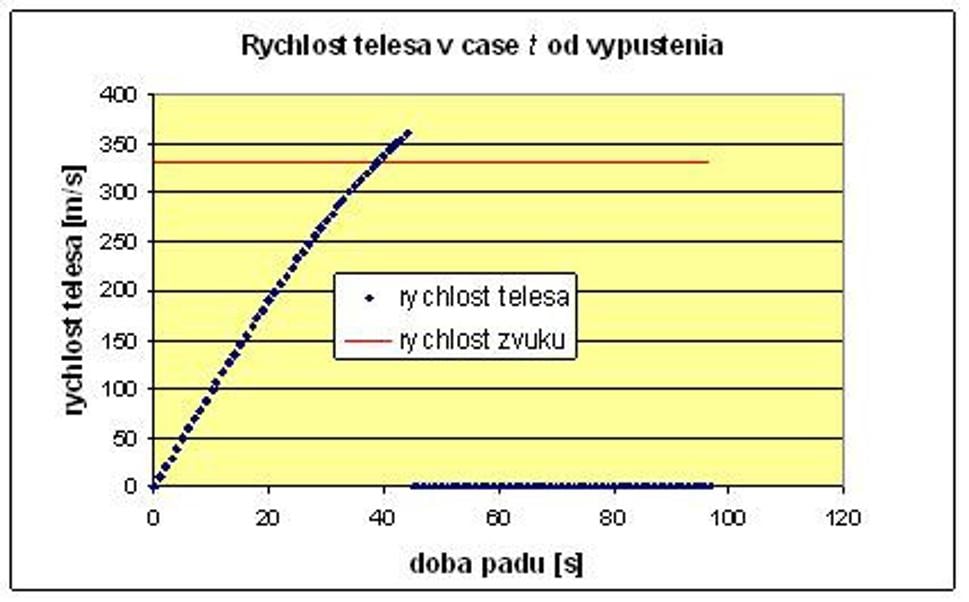
Odporová sila počas celej doby pádu nedosiahne anipolovicu tiažovej sily, teda zrýchlenie, s ktorým guľa padá, neklesne anio polovicu, ako vidno z nasledujúcich grafov.
A aký je záver? Rýchlosť zvuku sa v zemskej atmosféreaj pri odpore vzduchu prekonať dá. Akurát na to potrebujeme teleso, ktoré mádostatočne veľkú hmotnosť, vhodný tvar a musíme ho pustiť z dostatočneveľkej výšky.Nech sa páči, stiahnite si excelovský model a pohrajtesa:(Sorry za výzor tej stránky :-))
Nakoniec by som sa chcel poďakovať kolegom Števovi a Peťovi za inšpiratívny námet na rozmýšľanie a Dušankovi za diskusiu a pomoc pri problémoch s iteráciou.






