Galileo (1564-1642) sa narodil v talianskom meste Pisa, kde istý čas pôsobil aj na tamojšej univerzite. Napriek tomu, že začal študovať medicínu postupom času ho čoraz viac lákala matematika a mechanika. Veľa času strávil najmä nad prácami Euclida a Archimedesa a prostredníctvom knihy napísanej Gerolamom Cardanom sa dostal aj k problémom mechaniky, ktorým sa venoval Leonardo da Vinci. Svoje nazhromaždené poznatky o mechanike a pevnosti materiálov, ako aj výsledky svojich jednoduchých experimentov nakoniec zhrnul vo svojej knihe: Rozpravy a matematické dôkazy o dvoch nových odvetviach vedy, týkajúce sa mechaniky a miestnych pohybov.

Časť knihy, ktorá sa venuje problémom mechaniky a pevnosti materiálov sa považuje za prvú knihu z tejto oblasti. Rokom jej vydania (1638) sa zrodil odbor pružnosti a pevnosti, ktorý je jedným zo základných pilierov statiky.
V tejto knihe Galileo ako prvé zadefinoval tvz. maximálnu pevnosť materiálu stanovenú ťahovou skúškou podľa schémy č.1. Jednducho zvyšoval zaťaženie pokiaľ sa prút neroztrhol a údaje si zapisoval. Po odskúšaní viacerých prútov rôznych rozmerov dospel k prvým správnym záverom:
Odolnosť prierezu je priamo úmerná jeho prierezovej ploche (teda čím väčší prierez, tým viac unesie a to priamo úmerne svojej ploche). Túto silu nazval absolútna odolnosť proti zlomeniu (absolute resistance to fracture).
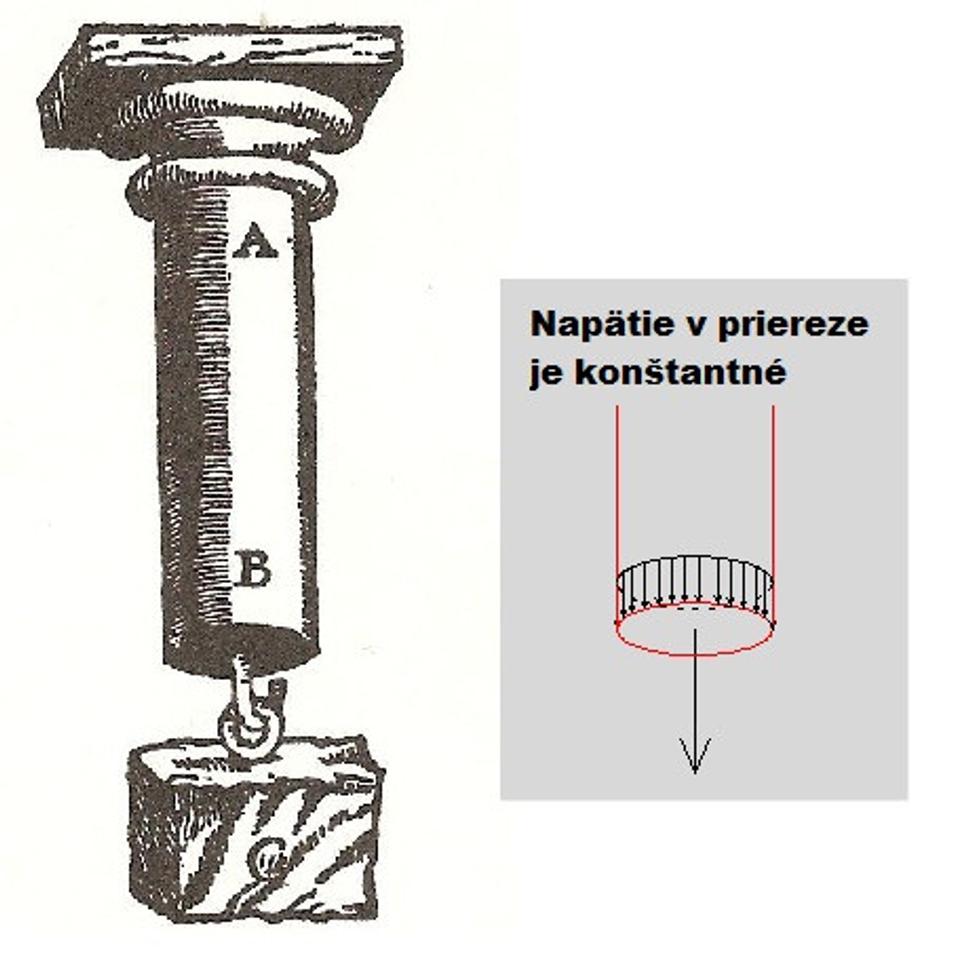
Túto hodnotu potom používal ako základ aj pri skúškach nosníkov na ohyb podľa schémy:
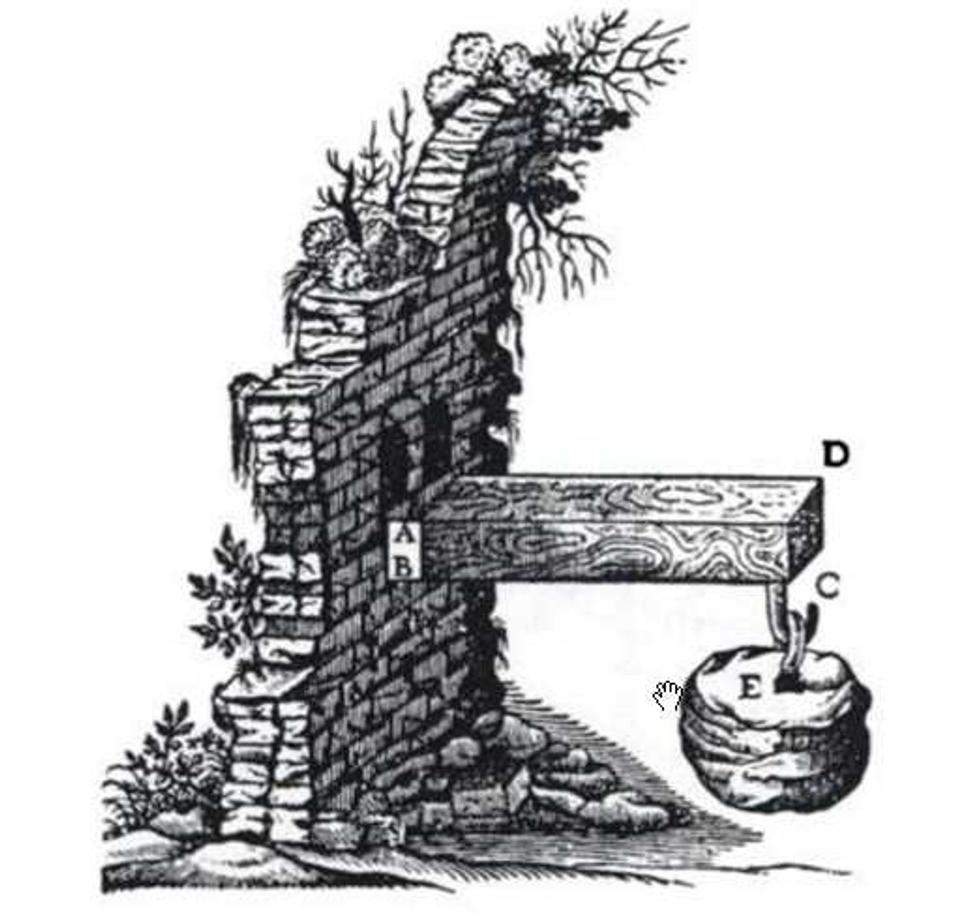
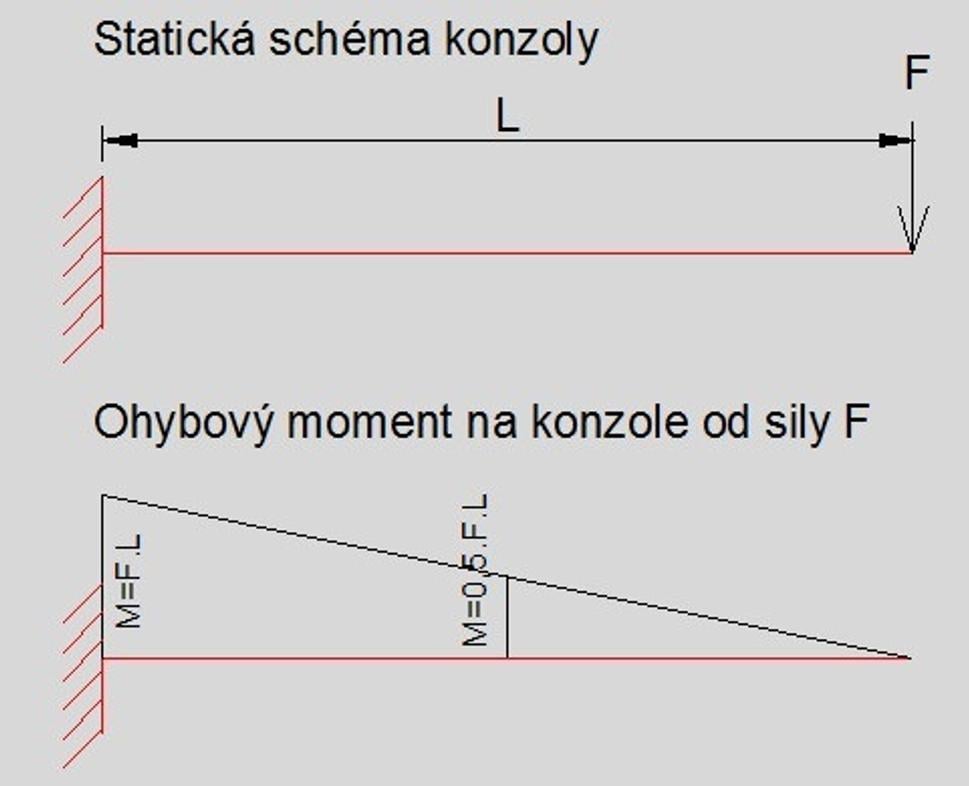
(V ďalšom texte sa pomerne často vyskytne termín: ohybový moment ... je to násobok sily na pôsobiacom ramene .... napr. na obrázku je ohybový moment od tiaže závažia v mieste ukotvenia konzoly v stene rovný: tiaž závažia x dĺžka BC .. ... teda vždy: moment = sila x rameno). V blogu sú tiež linky na odvodenie niektorých vzťahov, kto sa na to necíti môže ich kľudne ignorovať.
Vo svojej knihe píše: Je jasné že takto ohýbaný prvok sa zlomí v mieste ukotvenia do steny, kde prvok vzdoruje ohybovému momentu z ramena BC na ramene polovičnej dĺžky z AB (skrátená verzia).
Pri svojich výpočtoch odolnosti prierezu však Galileo spravil jednu chybu a to v úvahe, že tvz. napätie je po výške nosníka rovnomerné. Ak by sme teda aplikovali jeho vzorce na krehký materiál (napr. na sklo) skutočná únosnosť by bola len 1/3 z únosnosti vypočítanej Galileom. Keďže ale materiály ktoré pri svojich experimentoch používal dokážu prenášať silu aj po dosiahnutí max. napätia v krajnom vlákne (a prierez môže teda tvz. zplastizovať) jeho výpočet nebol ďaleko od pravdy. (vzorce1)
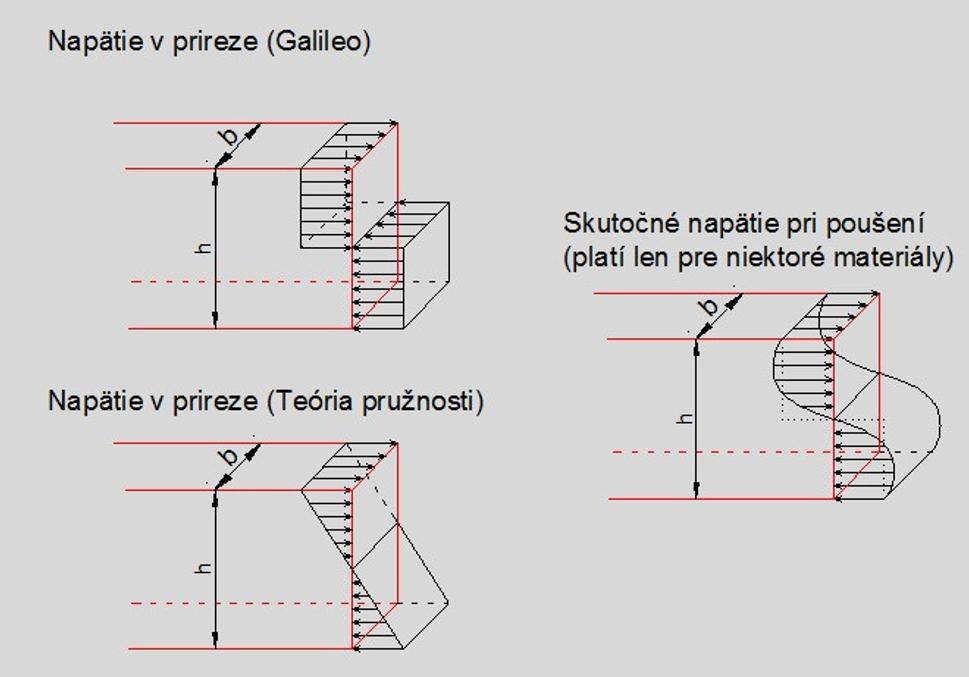
Správny vzorec z teórie pružnosti bol odvodený až v roku 1713 Antoinom Parentom.
Aj keď výpočet nebol úplne správny, na základe neho urobil potom niekoľko korektných a veľmi dôležitých záverov. Napr.: doska položená na výšku unesie väčšie zaťaženie ako doska položená na šírku a to presne v pomere strán h/b. Ak teda máme dosku 2 x vyšiu ako širšiu a postavíme ju na užšiu hranu unesie dvakrát väčšie zaťaženie ako keď ju položíte na ležato. (vzorce2)
Pre konzolu zase vyslovil správny záver o ohybovom momente od vlastnej tiaže: ohybový moment na konzole od vlastnej tiaže stúpa s druhou mocninou dĺžky. Platí to pre akékoľvek rovnomerné zaťaženie (napríklad ak na konzolu môžete rovnomerne naukladať jeden rad vriec, tak na konzolu polovičnej dĺžky rovnakých rozmerov môžete naukladať až 22 radov vriec (4-násobok oproti dlhej konzole). Konzola tretinovej dĺžky teda unesie analogicky 32 radov vriec (9-násobok dlhej konzoly). (vzorce3)
Ďalším veľmi zaujímavým zistením bol fakt, že ak zväčšujeme dĺžku a rozmery nosníka, jeho odolnosť voči ohybovému momentu narastá výrazne pomalšie ako ohybový moment od jeho vlastnej tiaže. Túto závislosť nakoniec spočítal a zistil, že ak chcete zabezpečiť únosnosť vlastnej tiaže nosníka, pri zväčšovaní jeho dĺžky, musíte jeho výšku zvačšovať s druhou mocninou zväčšovania jeho dĺžky (teda nie priamo úmerne). (vzorce4) Pr.: ak nosník výšky 30 cm sa od vlasnej tiaže zlomí pri dĺžke 5 metrov tak ak chceme aby uniesol svoju vlastnú váhu pri dĺžke 20 metrov, musíme jeho výšku zväčšiť na viac ako 480 cm (16 krát). Dokázal tým že sa nedá donekonečna zväčšovať rozpätia zvačšovaním rozmerov prierezu.
Podobná úvaha platí aj pre pomer momentov od vlastnej tiaže a zvyškovou momentovou odolnosťou prierezu. Analógiu na tento fakt našiel aj v prírode. Opísal to približne takto: malý pes unesie na chrbte možno až troch takých psov ako je on sám no kôň neunesie na chrbte ani čo i len jedného koňa (Pr.: ak je kôň 5 násobne väčší ako pes, museli by jeho kosti byť cca 25 násobne hrubšie ako u psa aby uniesol rovnaký násobok svojej váhy ... samozrejme existuje aj iná cesta a to buď voľbou pevnejšieho materiálu, iného tvaru prierezu, alebo konštrukčného systému).
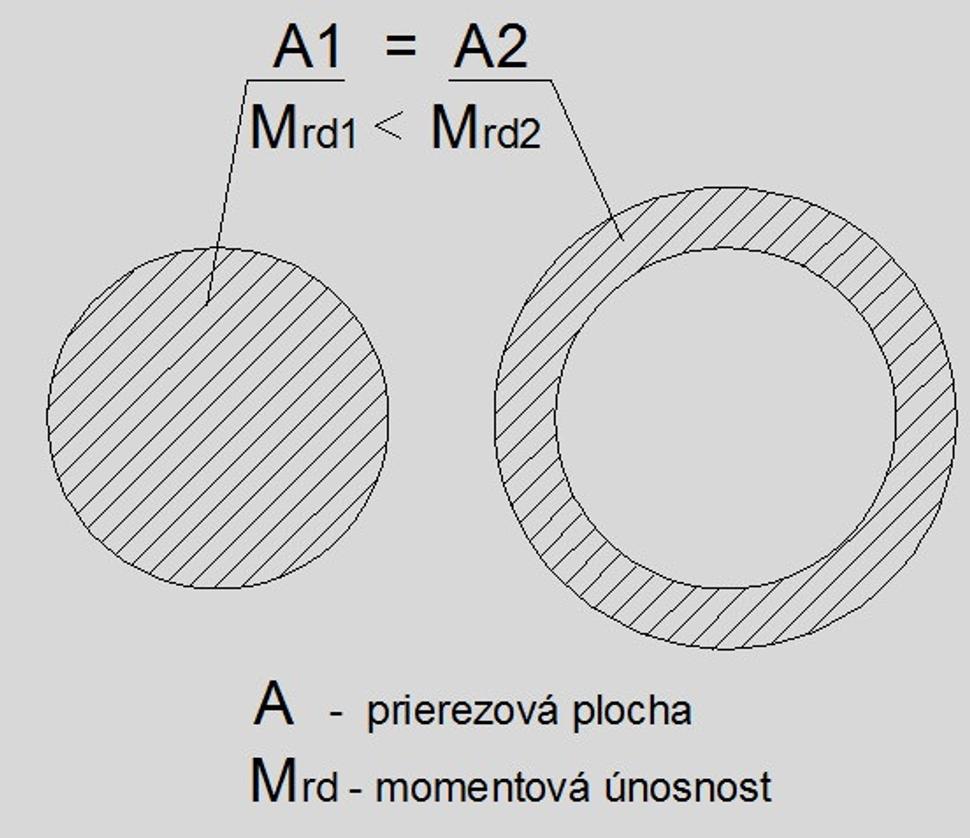
Neskôr sa vo svojej knihe venuje aj dutým prierezom, kde opisuje ich mnohé výhody. Tieto prierezy nachádza aj v prírode (napr. stonka rastlín). Ak máte dva prierezy s rovnakou prierezovou plochou ten dutý je v ohybovej odolnosti jednoznačne silnejší.
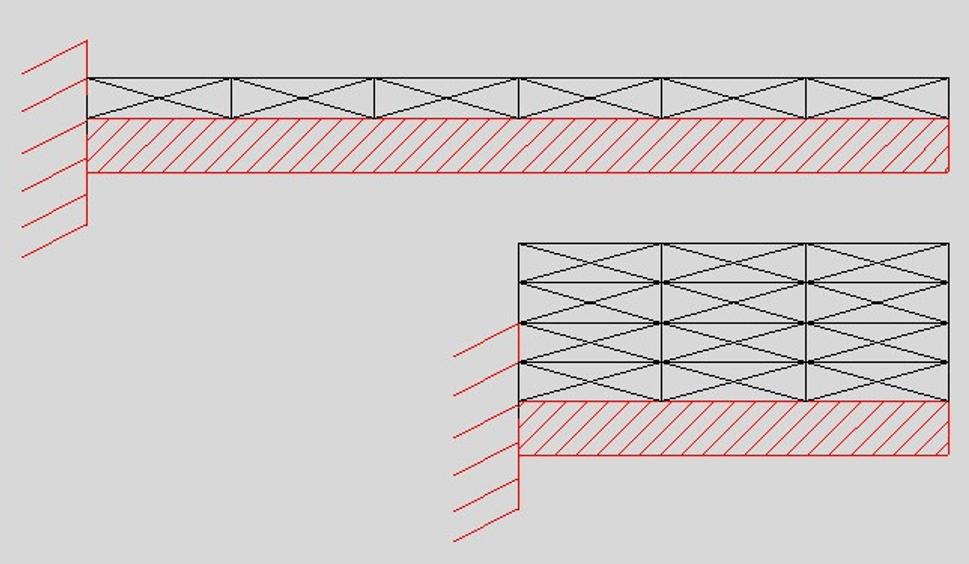
No a aby toho ešte nebolo dosť venoval sa aj tvz. optimalizácii prierezov po dĺžke nosníka.
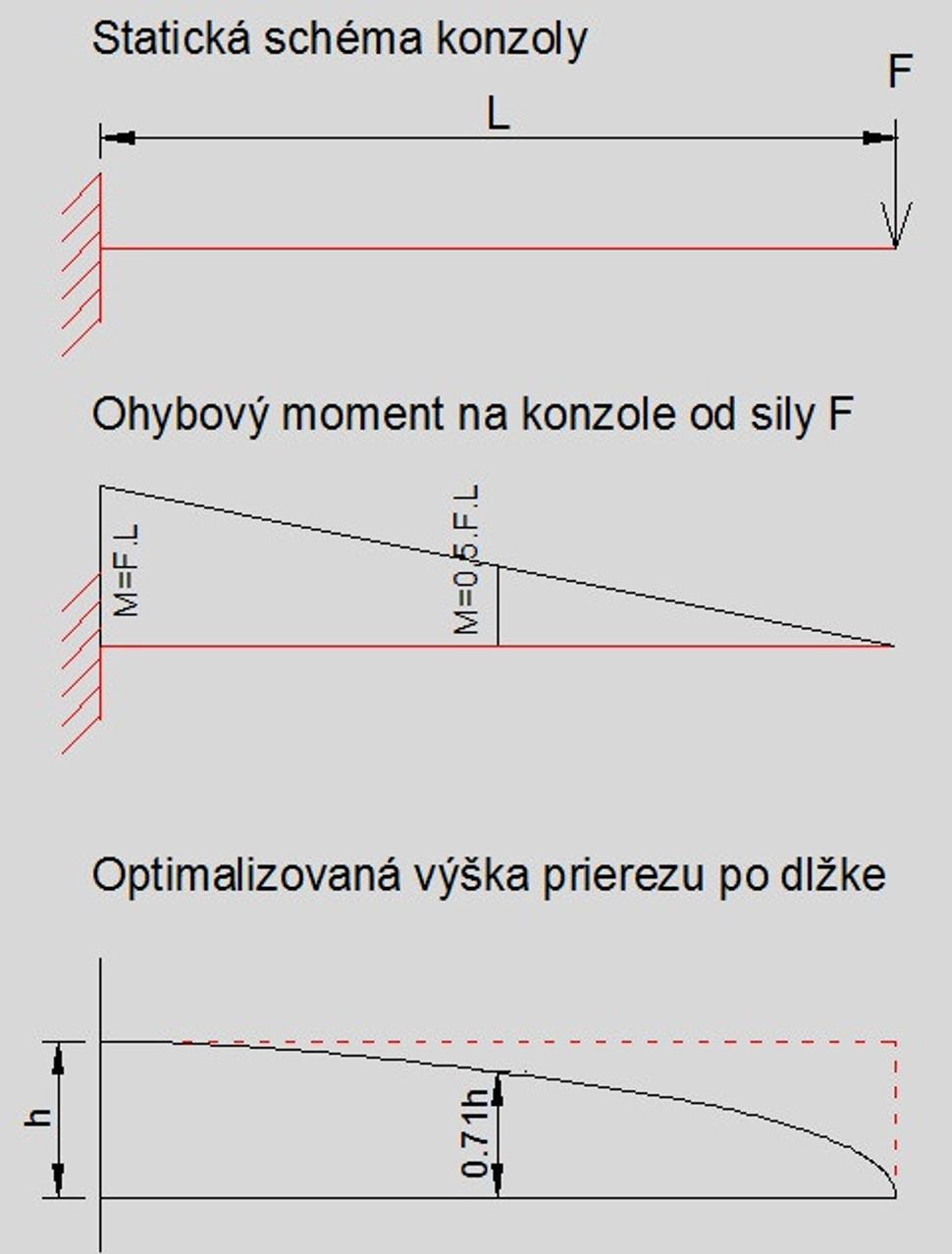
Ide o to že ak podľa Galileovej schémy navrhnete nejaký prierez na maximálny moment v mieste votknutia, už pár cm od tohto miesta nebude naplno využitý, pretože tam je už ohybový moment menší (sila pôsobí na menšom ramene). Optimalizovaný prierez je teda taký, ktorý je naplno využitý po celej dĺžke (postupne uberáte z jeho výšky).
Dokázal, že pre konzolu zaťaženú silou na konci nebude mať optimalizovaný prierez po dĺžke lineárny, ale parabolický priebeh (vyplýva to zo skutočnosti že 2-násobne vyšší prierez unesie až 4 násobne vyšší ohybový moment).
Galileo Galilei teda položil v 17.-tom storočí teoretické základy pevnosti materiálov a posunul tak aj stavbársku prax z obdobia navrhovania štýlom pokus-omyl do vyššej úrovne.
Blog bol pravdepodobne pre laika dosť zložitý, no väčšie zjednodušenia sa už spraviť nedali.






