Motivácia
Videli sme, že v elektrodynamike síce môžeme skonštruovať riešenie s helikálnou symetriou, ale toto riešenie je nefyzikálne, v prírode sa nerealizuje. Presunieme sa teraz do najzaujímavejšej teórie, ktorou je Einsteinova teória gravitácie, všeobecná teória relativity. Zatiaľčo v klasickej newtonovskej teórii helikálne symetrické riešenia existujú, vo všeobecnej relativite je situácia v zásade rovnaká ako v elektrodynamike. Prečo by sme sa teda mali zaujímať o takéto nefyzikálne riešenia? Súvisí to s problémom gravitačných vĺn.
Hoci je dnes všeobecná teória relativity (VTR) výborne preverená a otestovaná, existencia gravitačných vĺn, ktorú VTR predpovedá, doposiaľ nebola priamo overená. Je to preto, že gravitačné vlny sú extrémne slabé, o mnoho mnoho rádov slabšie než elektromagnetické vlny. Podobne ako nabitá častica vytvára pri pohybe po kružnici elektromagnetické vlny, aj Zem vytvára pri obiehaní okolo Slnka gravitačné vlny. Tie sú však tak slabé, že nemáme dnes najmenšiu šancu ich zmerať a potvrdiť. Zem sa pohybuje veľmi pomaly a je veľmi málo hmotná na to, aby produkovala merateľné gravitačné vlny.
Iná je situácia v prípade extrémne ťažkých a rýchlo sa pohybujúcich astrofyzikálnych objektov. Najsľubnejšími kandidátmi na intenzívny zdroj gravitačných vĺn sú binárne systémy pozostávajúce z čiernych dier alebo neutrónových hviezd, ktoré sme spomínali v úvode. Fyzici veria, že nasledujúca generácia detektorov gravitačných vĺn bude schopná zaznamenať gravitačné vlny budené takýmito objektmi.
Dobrá správa je, že týmto spôsobom boli už dávno gravitačné vlny potvrdené nepriamo. Pri pozorovaní objektov známych ako pulzary sa zistilo, že frekvencia ich obiehania sa s časom zvyšuje. To je spôsobené tým, že tieto objekty sa k sebe postupne približujú a polomer ich obiehania sa zmenšuje. Rýchlosť tohto približovania presne zodpovedá predpovediam Einsteinovej teórie, podľa ktorej postupné zbližovanie spôsobuje strata energie prostredníctvom vyžarovania gravitačných vĺn.
Takže nepriamo potvrdené gravitačné vlny sú: na ich existenciu poukazuje postupná strata energie pulzarov. Ale to je niečo iné, než zachytiť gravitačné vlny takého vzdialeného objektu priamo v pozemskom laboratóriu No dobre...nie nutne pozemskom...od roku 2015 by mala začať už raz odložená výstavba gravitačného detektora LISA umiestneného vo vesmíre. Rameno tohto detektora tvaru trojuholníka by malo mať 5 miliónov kilometrov...o čosi viac než je 27 kilometrov dlhý tunel urýchľovača LHC :)
Ale aj keď budeme mať detektory, ktoré budú schopné tu na Zemi (alebo blízkom okolí) detekovať gravitačné vlny, objavuje sa iný problém. Každý objekt vo vesmíre je zdrojom gravitačných vĺn a preto bude každé meranie zaťažené veľkým šumom, z ktorého bude ťažké identifikovať gravitačné vlny budené práve tým binárnym systémom, ktorý nás bude zaujímať. Preto musia experimentátory presne vedieť, ako majú gravitačné vlny budené binárnym systémom vyzerať. A preto sa teoretici snažia vyriešiť Einsteinove rovnice popisujúce binárny systém a zistiť čo najpresnejšie presnú formu gravitačných vĺn.
Numerická relativita
Einsteinove rovnice sú však po matematickej stránke nesmierne zložité a vyriešiť ich pre realistické problémy je nemožné. Musíme sa preto uchyľovať k numerickým metódam a približným výpočtom na počítačoch. Riešením Einsteinových rovníc na počítači sa zaoberá tzv. numerická relativita. I s použitím počítačov sa ale jedná o veľmi, veľmi ťažkú úlohu. Jednak na nejakú rozumnú simuláciu založenú na Einsteinových rovniciach treba veľmi výkonný počítač, dokonca tak výkonný, že aj dnes je to ešte problém.
Druhý problém spočíva v tom, že Einsteinove rovnice sú štvorrozmerné a popisujú geometriu priestoročasu. Ich elegancia je mimo iné v tom, že vyzerajú rovnako pre všetkých pozorovateľov a nerozlišujú medzi priestorovými a časovými súradnicami. To, čo potrebujeme, je však popis toho, ako sa systém vyvíja v čase a pre jedného konkrétneho pozorovateľa. Preto je potrebné Einsteinove rovnice neelegantne zase rozdeliť na priestorovú a časovú časť. Pretože priestor má 3 rozmery a čas 1, hovoríme o 3+1 rozklade Einsteinových rovníc. Hoci mám k dispozícii len laptop s euklidovskou obrazovkou, pokúsim sa znázorniť princíp 3+1 rozkladu neeuklidovskej geometrie na obrázkoch.
Začnime s plochým priestoročasom. Spomeňme si, že predchádzajúci článok sme zakončili obrázkom skrutkovice a popíšme trochu podrobnejšie, ako tento obrázok vznikol. Uvažujeme teraz nabitú časticu zanedbateľnej hmotnosti, takže môžeme zanedbať jej gravitačné pole, ktorá obieha po kružnici. Predstavme si, že celý priestor znázorníme jedinou rovinou, ako na tomto obrázku:
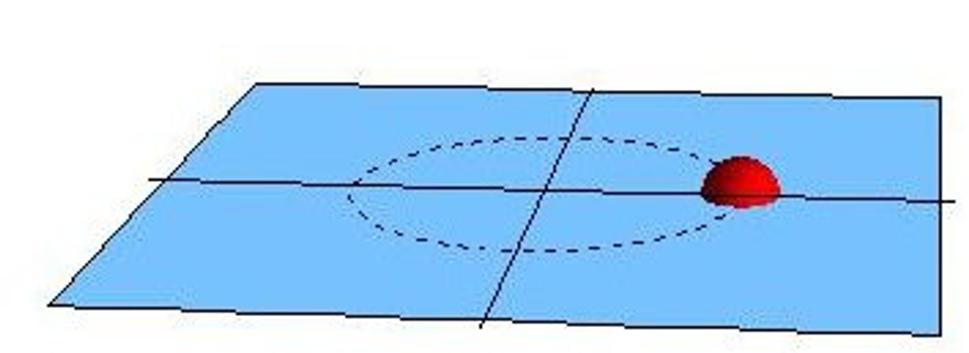
Máme teda trojrozmerný priestor (znázornený rovinou), v ktorom sa nachádza častica. Pretože rovina znázornená na obrázku je v skutočnosti trojrozmerná, budem ju naďalej označovať pojmom nadplocha alebo hyperplocha. Poloha častice sa s časom mení, takže v neskoršom čase bude tento obrázok vyzerať napríklad takto:
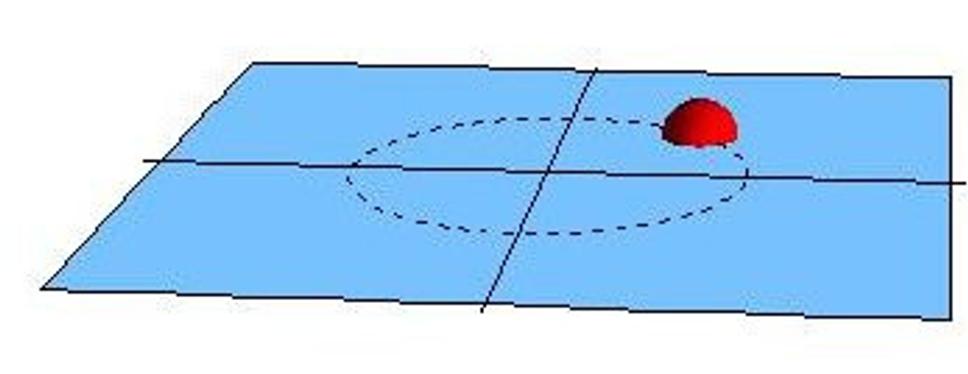
Myšlienka priestoročasu spočíva v tom, že pre každý čas t skonštruujeme príslušnú nadplochu, v ktorej bude mať častica svoju polohu v čase t. Získame tak nekonečne mnoho nadplôch, ktoré reprezentujú preistor vo všetkých možných časoch. Tieto nadplochy naukladáme nad seba v takom poradí, v akom nasledujú jednotlivé časy, takže získame nasledujúci obrázok:
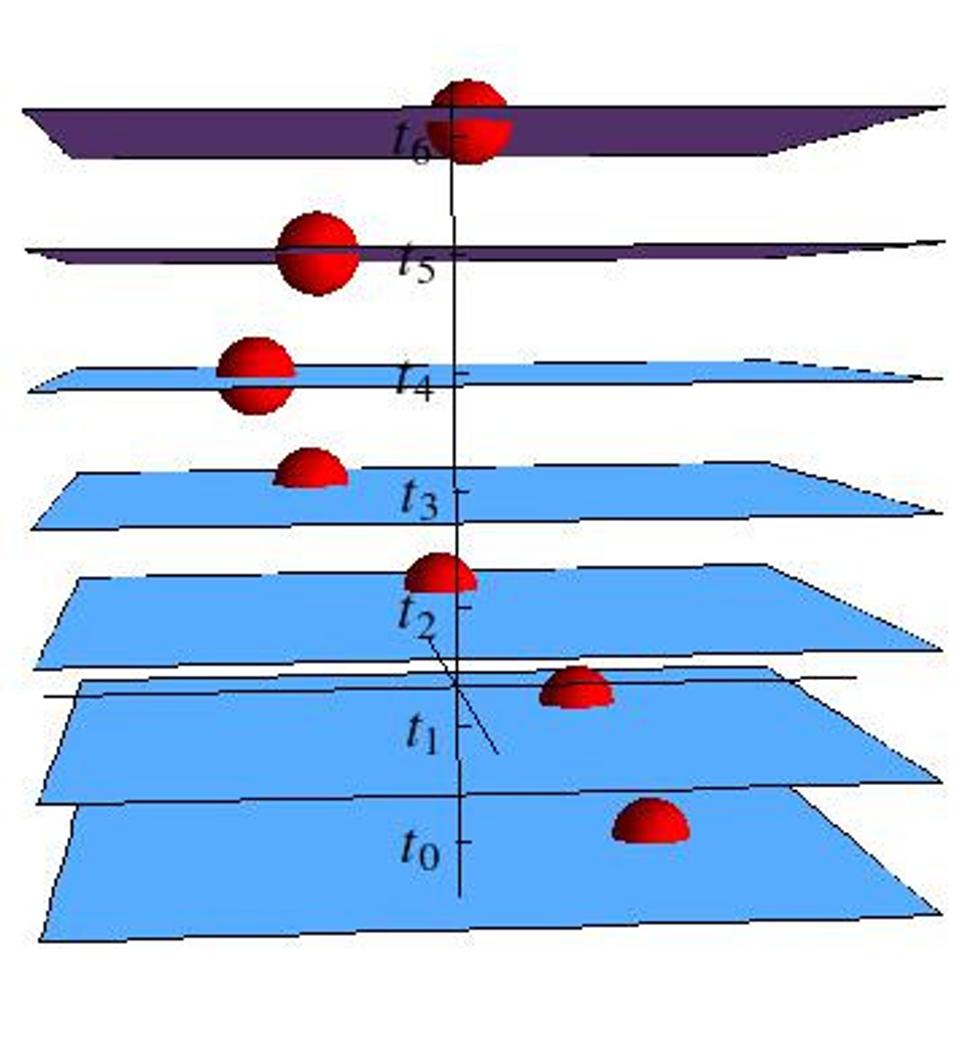
Na tomto obrázku čas plynie smerom nahor. Vidíme, že častica, ktorá sa v priestore pohybuje po kružnici, v priestoročase opisuje skrutkovicu:
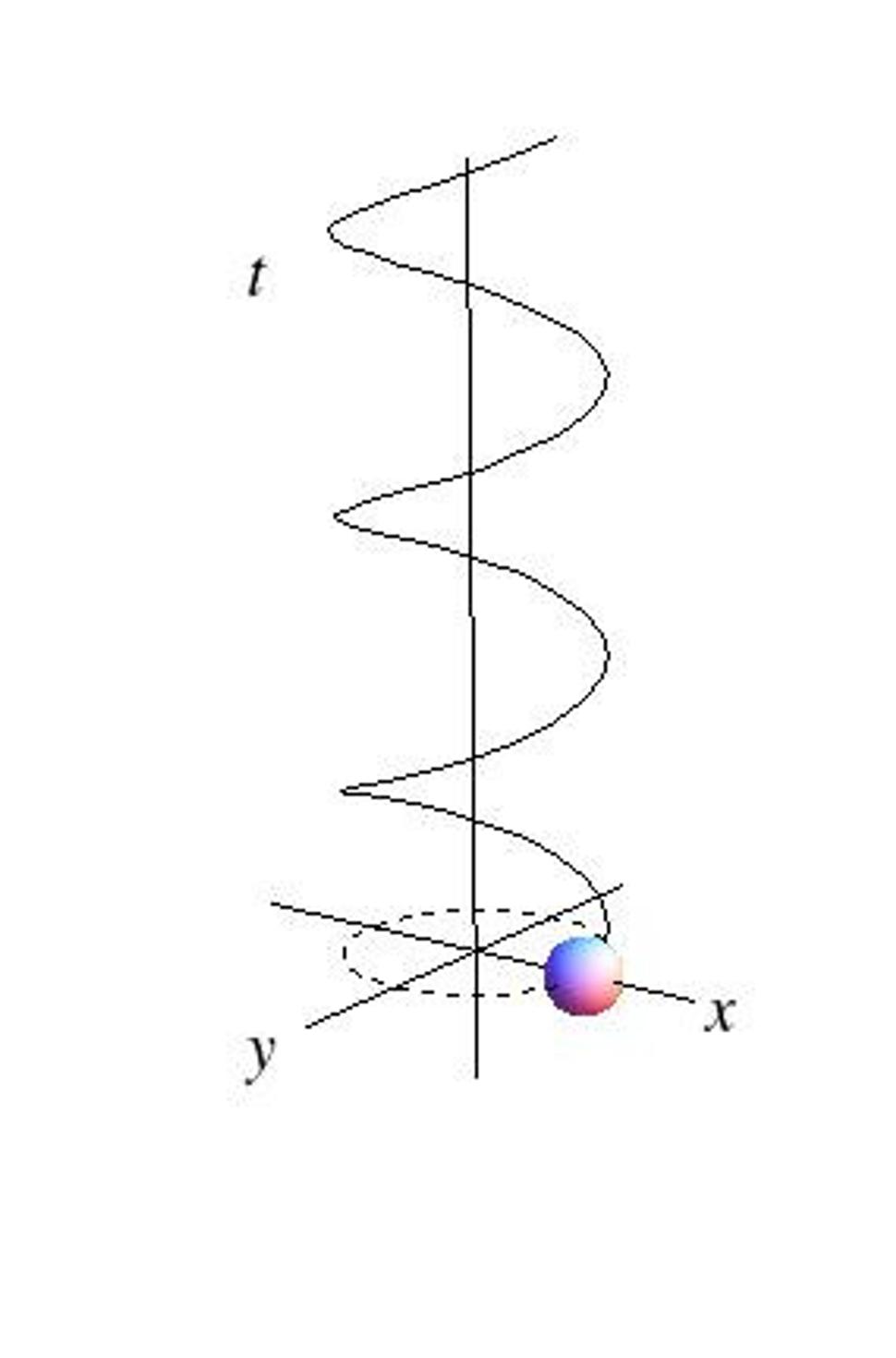
Trajektórii častice v priestoročase hovoríme svetočiara, aby sme ju odlíšili od skutočnej trajektórie v trojrozmernom priestore. Ak chceme z priestoročasového obrázka zistiť polohu častice v nejakom čase t, urobíme vodorovný rez priestoročasom rovinou kolmou k časovej ose, čím získame nadplochu reprezentujúcu priestor v tomto čase.
Takže ak máme časticu pohybujúcu sa po kružnici, jej svetočiara v priestoročase je skrutkovica. V minulom článku som uviedol, že od anglického prekladu slova skrutkovica (helix) sa odvíja pojem helikálnej symetrie. Zopakujem: systémy, v ktorých sa častice pohybujú po kružniciach, majú helikálnu symetriu. Otázka, ktorej sú tieto dva články venované, je nasledovná: môžu v relativite existovat helikálne symetrické systémy?
V uvedenom príklade sa jednalo o plochý priestoročas, zvaný aj Minkowského priestoročas, pretože sme neuvažovali gravitáciu. Einsteinova fascinujúca myšlienka je, že gravitácia je v skutočnosti prejav geometrie priestoročasu. Ak sa v priestore nachádzajú zdroje gravitačného poľa, zakrivujú geometriu priestoročasu a ten prestáva byť plochý. Priestor v nejako počiatočnom čase si teda možno názorne predstaviť ako zakrivenú plochu, nie ako rovinu. Ako som už naznačil, krása Einsteinových rovníc spočíva v tom, že popisujú priamo geometriu celého priestoročasu a nerozlišujú medzi časovými a priestorovými súradnicami. Výhodou je, že tento popis automaticky zahrnuje všetkých možných pozorovateľov. Rôznym pozorovateľom a ich časom zodpovedajú rôzne rezy priestoročasu.
Keď ale chceme riešiť Einsteinove rovnice na počítači, takýto elegantný prístup nikam nevedie. Počítač vždy potrebuje nejaké začiatočné dáta, ktoré sa potom vyvíjajú v čase. Počítač teda pracuje podobne, ako sme v predchádzajúcom príklade konštruovali skrutkovicu. Začali sme v čase nula, zostrojili sme príslušnú nadplochu, umiestnili do nej časticu, a potom sme skúmali, ako sa poloha častice mení s časom. A v každom čase sme zostrojili novú nadplochu, ktorá reprezentovala priestor v tomto čase.
V numerickej relativite sa postupuje podobne, ale s tým, že tentoraz sa nezaujímame priamo o polohy častíc, ale o geometriu priestoru. Na začiatku teda zvolíme nejakú nadplochu a predpíšeme jej geometriu podľa toho, aký problém práve skúmame. Potom rozložíme Einsteinove rovnice na dve časti: na trojrozmernú, ktorá popisuje geometriu priestoru, a na časť, ktorá popisuje, ako sa táto geometria bude vyvíjať v čase. Veľmi symbolicky si to môžeme predstaviť takto:
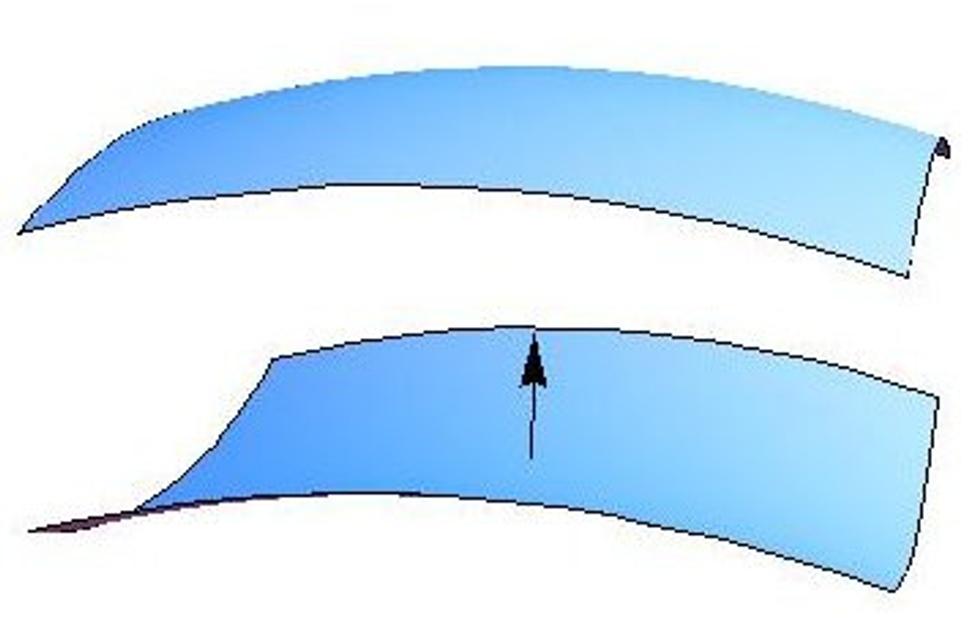
Spodná nadplocha (ktorá už nie je rovinou), predstavuje geometriu priestoru v čase 0, šípka znázorňuje smer času. V nejakom neskoršom čase potom dostaneme novú nadplochu (zvlnenú vo všeobecnosti inak), ktorá reprezentuje priestor v tomto neskoršom čase.
Technický, ale veľmi dôležitý problém je, že geometriu počiatočnej nadplochy nemožno zvoliť úplne ľubovoľne, ale tak, aby vyhovovala priestorovej časti Einsteinových rovníc, tzv. väzbám. Tieto väzby sú samé o sebe dosť komplikované, takže v numerickej relativite je ťažké už len sformulovať problém, ktorý vlastne chceme riešiť.
Ale je tu ešte jedna vec, a tá už sa úzko dotýka nášho problému s binárnymi systémami. V minulom článku sme zdôraznili, že v relativistických teóriách sa nič nemôže pohybovať rýchlejšie než svetlo. Ani gravitačné pole. To znamená, že ak dôjde k nejakej zmene gravitačného poľa ( = geometrie nadplochy), táto zmena sa len postupne, rýchlosťou svetla, šíri do okolia. Všimnime si nasledujúci priestoročasový obrázok:
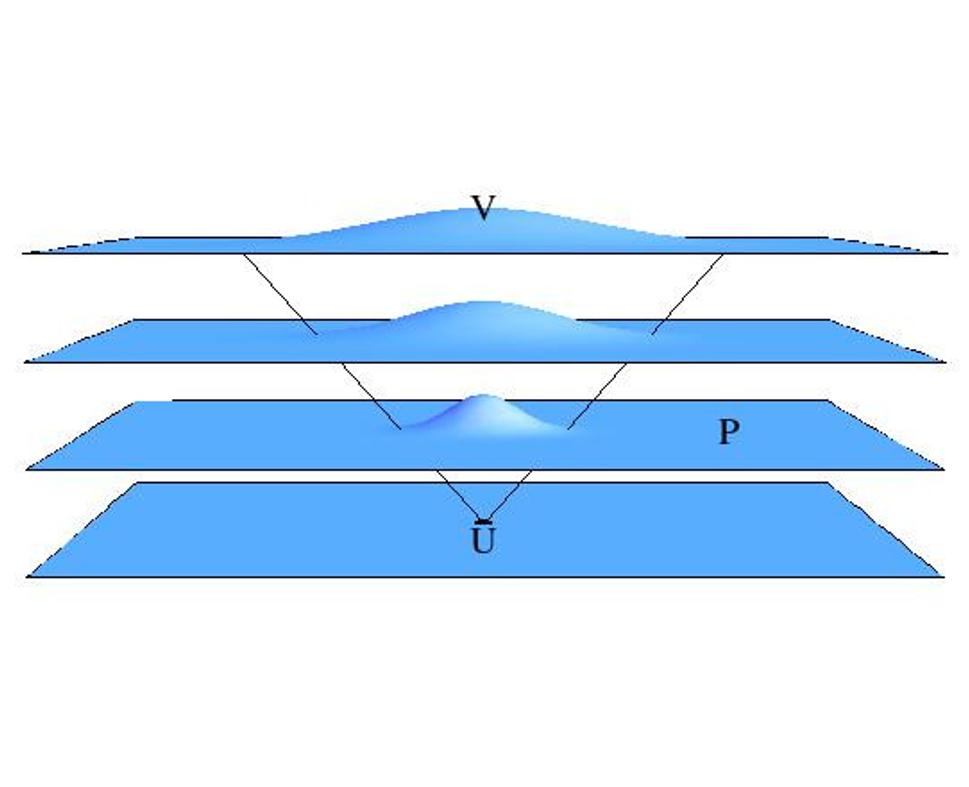
Úplna spodná nadplocha zodpovedá plochému priestoru v čase nula. Predpokladajme, že sa z nejakého dôvodu začne šíriť z tohoto bodu gravitačná vlna, ktorá spôsobuje deformácie priestoru. Vznik gravitačnej vlny v čase nula sme označili ako udalosť U. Ďalšie nadplochy znázorňujú, ako sa táto gravitačná vlna s časom šíri priestorom. Pretože gravitačná vlna sa šíri rýchlosťou svetla, je zrejmé, že v každom čase môže gravitačná vlna doraziť len do určitej vzdialenosti od zdroja. Čelo gravitačnej vlny a jeho pohyb v čase sú znázornené dvoma čiernymi priamkami, ktoré sa pretínajú v bode U - udalosti vzniku gravitačnej vlny. Tieto čierne priamky definujú tzv. budúci svetelný kužel a ich zmysel je nasledujúci: udalosť U môže ovplyvniť LEN udalosti, ktoré sa nachádzajú vo vnútri svetelného kužeľa. Napríklad udalosť P znázornená na druhej nadploche nemôže byť nijak ovplyvnená vznikom gravitačnej vlny v udalosti U.
Položme si naopak otázku, ktorými udalosťami v minulosti môže byť ovplyvnená udalosť V znázornená na štvrtej nadploche. Sú to všetky udalosti, z ktorých mohlo svetlo (gravitačná vlna) dospieť až do udalosti V. K tomu môžeme zostrojiť minulý svetelný kužeľ:
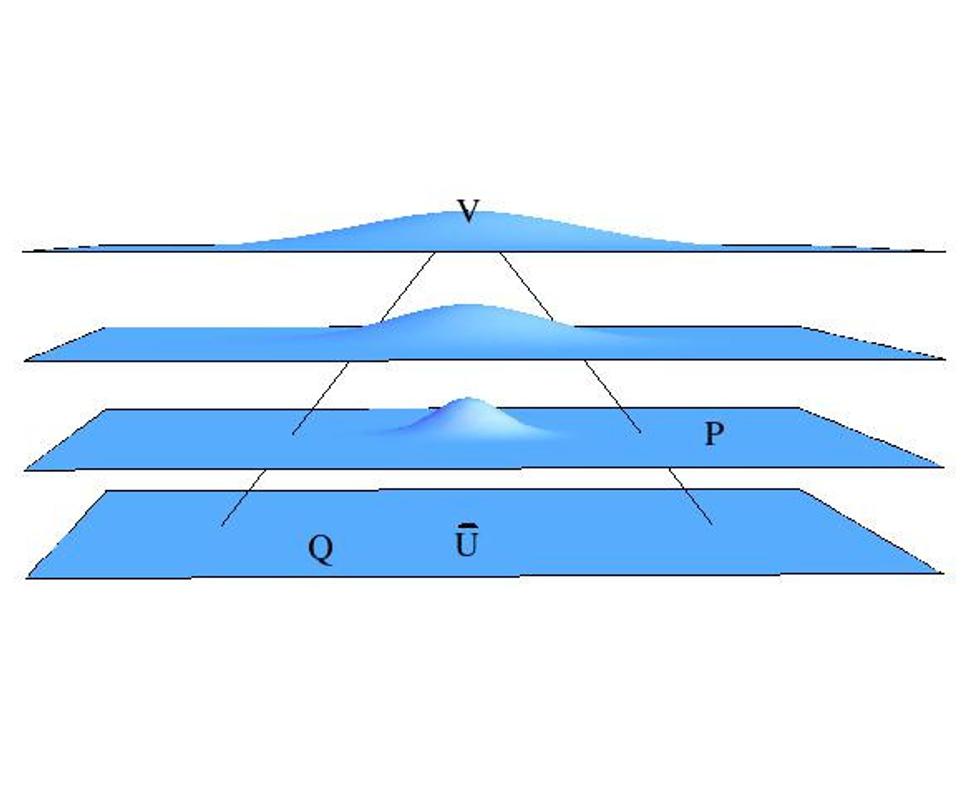
Na tomto obrázku vidíme, že udalosť V je ovplyvnená nie len udalosťou U, v ktorej gravitačná vlna vznikla, ale aj nejakým jej okolím. Ale svetelný kužeľ sa nezastavuje na nadploche, kde udalosť U leží. Naopak, rozprestiera sa až do nekonečne vzdialenej minulosti a všetky udalosti ležiace v minulom svetelnom kuželi majú potenciálne vplyv na udalosť V. Inými slovami, aj keď nás zaujíma len vývoj gravitačnej vlny vzniklej v bode U, na toto šírenie môžu mať v princípe vplyv všetky udalosti ležiace v minulom svetelnom kuželi.
A to je pre numerickú relativitu problém. Aby sme mohli modelovať budúcnosť, musíme do detailov poznať vlastne celú minulosť. To v praxi nie je možné a preto je treba minulý svetelný kužeľ niekde "utnúť" a predpísať vhodné okrajové podmienky. To, ako tieto podmienky zvoliť, je celá veda. Helikálna symetria je jeden zo spôsobov, ako numericky riešiťproblém binárnych systémov.
Kolabujúce binárne systémy
Toto je záverečná sekcia dvojice článkov na tému Binárne systémy. Preto ešte naposledy zrekapitulujem, o čo šlo.
Z newtonovskej teórie gravitácie vieme, že objekty (planéty, hviezdy, ...) môžu obiehať donekonečna po kružnici. Ale newtonovská teória nie je adekvátna pre popis astrofyzikálnych objektov, namiesto toho musíme použiť Einsteinovu všeobecnú teóriu relativity. Pretože tá je veľmi zložitá, vyjasnili sme si v minulom článku, ako to je v jednoduchšej špeciálnej teórii relativity (bez gravitácie) a ako príklad sme uvažovali nabité častice. Môžu nabité častice donekonečna obiehať po kružnici?
V minulom článku sme videli, že to nie je možné. Pohybujúce sa náboje budú vyžarovať elektromagnetické vlny, čím strácajú energiu a nutne padajú do stredu obiehania. Videli sme však tiež to, že matematickou fintou je možné docieliť, aby na časticu dopadalo vonkajšie žiarenie, ktoré by presne kompenzovalo stratu energie vyžarovaním. Ak takéto žiarenie zavedieme, dostaneme časticu obiehajúcu po kružnici, teda systém s helikálnou symetriou. Zároveň sme ale povedali, že takéto riešenie je nefyzikálne, pretože dopadajúce žiarenie musíme modelovať signálom, ktorý cestuje späť v čase.
Vo VTR (všeobecnej teórii relativity) je to veľmi podobné, ako som zahlásil hneď na úvod tohto článku. Dve neutrónové hviezdy alebo čierne diery nemôžu donekonečna obiehať po kružnici, pretože budú vyžarovať gravitačné vlny (teda vlny, ktoré sa prejavia "vlnením" priestoročasovej geometrie). A práve tieto vlny sú z fyzikálneho hľadiska zaujímavé: dúfame, že binárne systémy pozostávajúce z extrémne hmotných objektov nám umožnia zachytiť nimi produkované gravitačné vlny tu na Zemi.
Aby sme ale vedeli, aké vlny máme od takého systému očakávať, musíme pochopiť celý proces najprv teoreticky. Je beznádejné skúšať vyriešiť Einsteinove rovnice pre tento prípad presne, takže musíme použiť počítač. V minulej sekcii som naznačil, ako numerická relativita funguje a aké sú jej úskalia. Okrem technických problémov, ktorých je viac než dosť, sme v závere predchádzajúcej sekcie narazili na jeden vážnejší fyzikálny problém: aby sme mohli nasimulovať vývoj binárneho systému, musíme poznať celú jeho minulosť. To v praxi nie je možné.
Ale práve tu nám veľmi pomôže pojem helikálnej symetrie, o ktorom celý čas hovoríme a odvrhujeme ho ako nefyzikálny. Je fakt, že systémy s helikálnou symetriou nemôžu existovať. Ale je tiež fakt, že mnohé binárne systémy po dlhú dobu môžu byť približne helikálne symetrické. Ako príklad uveďme jeden z najznámejších pulzarov, PSR B1913+16. Pozostáva z dvoch neutrónových hviezd, z ktorých jedna je pulzarom, takže vysiela elektromagnetické vlny. Tieto vlny sú koncentrované do pomerne úzkeho zväzku, takže ho môžeme vidieť, len keď ukazuje presne smerom k Zemi. Preto namiesto súvislého žiarenia vidíme len krátke impulzy - preto pulzar. Perióda týchto impulzov by mala byť konštantná, ale v skutočnosti sa s časom periodicky mení. Tak sa prišlo na to, že tento pulzar musí byť súčasťou binárneho systému, takže blízko neho je iná neutrónová hviezda (nie pulzar) a obe neutrónové hviezdy spolu obiehajú okolo spoločného ťažiska.
V súlade s VTR sa obe neutrónové hviezdy k sebe postupne približujú, pretože vyžarujú gravitačné vlny a teda strácajú energiu. V skutočnosti sa teda obe hviezdy nepohybujú po kružniciach, ale po špirálach. Výpočty však ukazujú, že ku konečnej zrážke oboch hviezd dôjde až za 300 miliónov rokov! Je inak úžasné, že tak pomalý proces sa dá tak presne merať.
To ale znamená, že ak sledujeme túto dvojhviezdu pár rokov, zistíme, že sa obe hviezdy pohybujú skoro po kružnici. Ak chceme simulovať na počítači celý proces zbližovania dvojhviezd a ich pádu po špirále do stredu, môžeme na začiatku predpokladať, že hviezdy sa odjakživa pohybujú presne po kružniciach. To znamená, že na začiatku predpokladáme, že máme systém s helikálnou symetriou. Tým obídeme problém s okrajovými podmienkami, o ktorom sme hovorili. Spomeňme si, že na to, aby sme niečo nasimulovali, potrebujeme vedieť celú minulosť danej sústavy. No tak tu si ju predpíšeme: predpokladáme, že od času "mínus nekonečno" má dvojhviezda helikálnu symetriu. Samotná helikálna symetria je nefyzikálne riešenie, ale veľmi dobre poslúži ako štartovací bod. Je fyzikálne zrejmé, že ak nás zaujíma konečný osud dvojhviezdy, nebude príliš podstatné (alebo vôbec podstatné), ako presne dvojhviezda vznikla, koľko rokov obiehala, aký fúkal vietor, a tak podobne. Máme teda výborné počiatočné podmienky, ktoré veľmi dobre vystihujú skutočný stav vecí a navyše obchádzajú problém okrajových podmienok.
Skutočná numerická simulácia potom vyzerá takto. Predpokladá sa presná helikálna symetria binárneho systému, takže obe hviezdy obiehajuú presne po kružniciach:
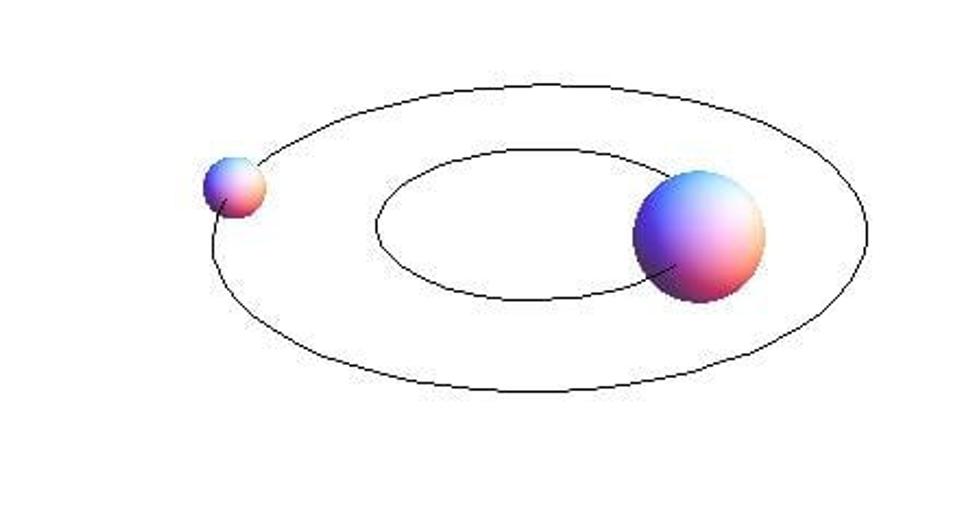
Simuláciu necháme nejaký čas bežať a potom umelo porušíme polomer obiehania, ale stále požadujeme helikálnu symetriu.
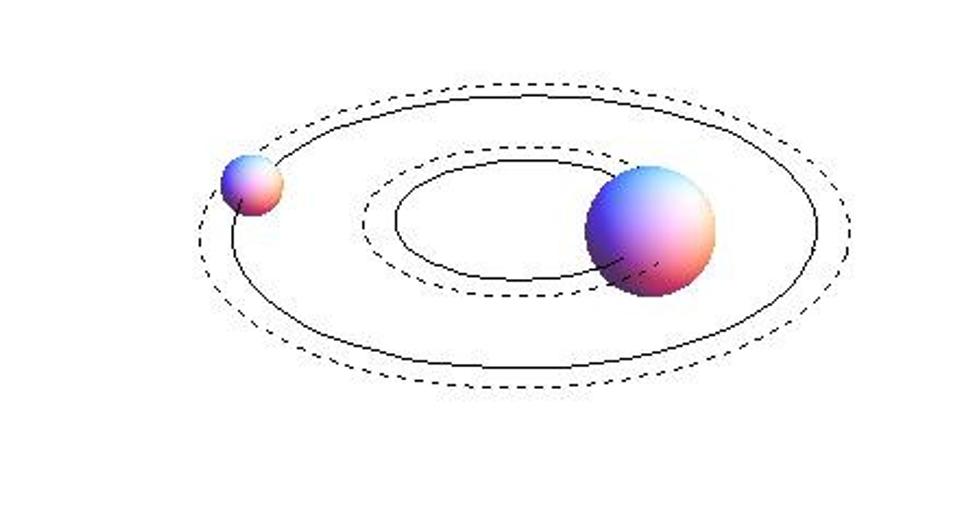
Celý proces sa niekoľko krát opakuje, takže dostaneme postupnosť rovnovážnych (helikálne symetrických) pohybov systému:
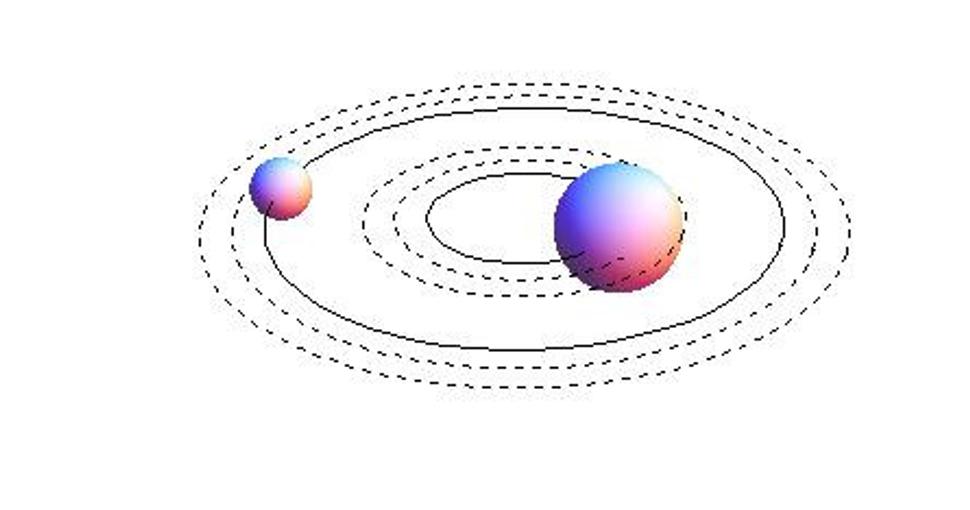
Týmto postupom sa vytvoria vhodné počiatočné podmienky pre simuláciu samotného procesu kolapsu. Keď hviezdy prekročia určitú hranicu známu ako ISCO (innermost stable circular orbit, najvnútornejšia stabilná kruhová dráha), helikálna symetria prestane byť vhodným priblížením a nasleduje veľmi rýchly kolaps po špirále. Tento proces už nie je možné aproximovať a musíme použiť úplné Einsteinove rovnice. Dôvod, prečo nie je možné použiť úplné Einsteinove rovnice hneď od začiatku, má dve príčiny. Jedna je principiálna: potrebujeme systém dostať do vhodného začiatočného stavu, ako sme o tom pojednali vyššie. Druhá vec je, že vzhľadom na komplikovanosť Einsteinových rovníc dokáže ich počítač dostatočne presne riešiť len pomerne krátky čas. Použitie helikálnej symetrie rieši oba problémy: naaranžujeme vhodné počiatočné a okrajové podmienky a zároveň dostaneme systém tak blízko kolapsu, ako je to len možné. Na Eisnteinových rovniciach potom už spočíva len ťarcha simulácie najzaujímavejšej časti procesu. V tejto záverečnej fáze sa produkuje ohromné množstvo gravitačných vĺn a veríme, že v dohľadnej dobe budeme mať detektory, ktorými ich zachytíme.
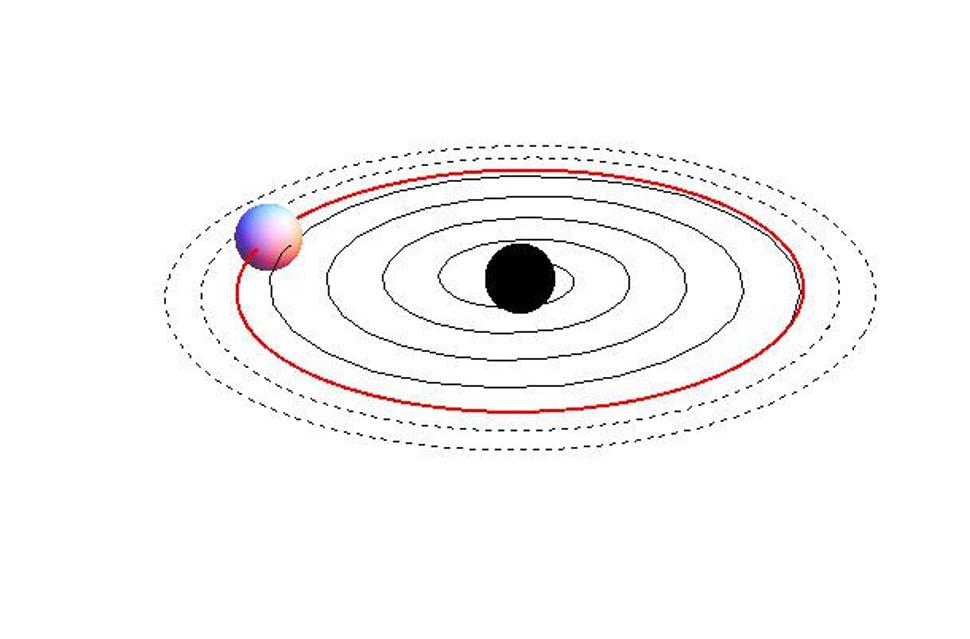
Na tomto obrázku je pre prehľadnosť znázornená len jedna zložka binárneho systému. Na konci kolapsu sa obidve hviezdy zrazia v ťažisku a vytvoria novú čiernu dieru. Prebytočná energia sa vyžiari v podobe gravitačných vĺn.
Tak a teraz si už môžete sami doma nasimulovať celý proces. S chuťou do toho! :)
Ďakujem za pozornosť.






