
Spor vznikol z reálneho pozorovania otca. Tvrdil, že keď bol naposledy v Bratislave a bola výnimočne dobrá viditeľnosť, videl vzadu na horizonte rakúske Alpy. Ja som ochotne prebral pozíciu oponenta tohto tvrdenia s tým, že také niečo kvôli zakriveniu Zeme nie je možné.
Vychádzal som však skôr z vlastnej skúsenosti, že z Bratislavy tieto hory nie sú vidieť ako z nejakého exaktného matematického výpočtu. Druhá indícia, ktorá mi nahrávala boli oblaky. Na bielo žiariace kumuly umiestnené na horizonte, počas jasného dňa s dobrou viditeľnosťou dokážu oklamať aj oko odborníka a vytvoriť dojem na horizonte trčiacich zasnežených skál. Niečo mi tu však nesedelo - u otca som málokedy pozoroval, žeby sa v takýchto otázkach mýlil (a dokázalo ma to aj patrične rozčúliť), hoci vždy vychádzal len zo zdravého sedliackeho rozumu. A tak aj keď som horlivo zastával názor, že sa nechal detinsky oklamať oblakmi, stále vo mne vŕtala pochybnosť (tú som samozrejme na sebe nemohol počas našich diskusií dať poznať). Preto som sa nakoniec rozhodol urobiť pár drobných výpočtov a tu je výsledok :
Vychádzame z ideálneho prípadu, Zem je guľa s polomerom 6372795,5m (stredná hodnota pre polomer Zeme), na ktorej sa nachádzajú len dve nerovnosti: ja ako pozorovateľ o istej výške nad povrchom a pozorovaný objekt, tiež so svojou výškou. V prvom kroku budeme pozorovaný objekt pokladať za tyč s nulovou dĺžkou a vypočítame tým vzdialenosť ideálneho horizontu:
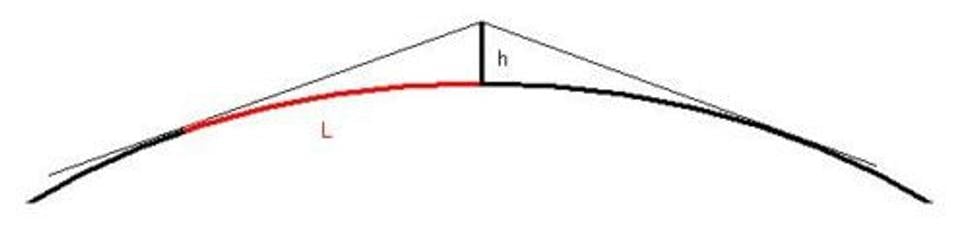
Pre človeka vysokého 2m je vzdialenosť horizontu na povrchu gule o polomere Zeme rovná asi 5,05km (jedná sa o dĺžku oblúka na povrchu gule, nie vzdušnú vzdialenosť, pozn. aut.). Čiže z centra Bratislavy toho veľa neuvidíme - maximálne tak po hranice s Rakúskom. Samozrejme, situácia sa dramaticky mení ak aj pozorovaný objekt má nejaké rozmery. Jednoduchou úvahou prídeme k výsledku, že dvaja 2-metroví ľudia na povrchu ideálnej Zeme na seba dovidia už vtedy, ak sa ich horizonty budú práve dotýkať (alebo budú stáť ešte bližšie) - čiže zo vzdialenosti 10,1 km:
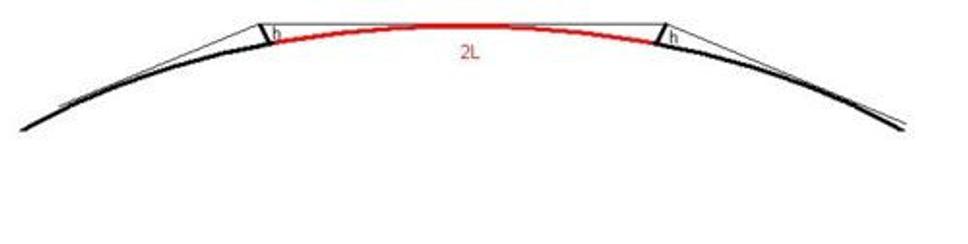
Možno by stálo zato to vyskúšať niekde na maďarskej puste. Napríklad s pomocou ďalekohľadu si to viem celkom reálne predstaviť a ďalekohľad nijako nemení geometrické usporiadanie pokusu.
No a prejdime teraz k spomínaným Alpám a Bratislave. Predhoria Álp začínajú už neďaleko Viedne. Tie nás však nezaujímajú, nakoľko tmavozelené listnaté alebo ihličnaté lesy z veľkej vzdialenosti dobre viditeľné nie sú. To, čo nás zaujíma sú zasnežené vrcholky hôr. Najvýchodnejšou dvojtisícovkou v Alpách je 2075 metrov vysoký Schneeberg:

Schneeberg, Rakúsko (http://lucenic.net/kammanohyzavedu/schneeberg.htm)
Vrch je od Bratislavy vzdialený asi 105 km (merané pozdĺž povrchu Zeme - vzdialenosť sa kvôli malému zakriveniu Zeme na takých krátkych vzdialnostiach príliš neodlišuje od vzdušnej čiary). Jeho nadmorskú výšku poznáme, už spomínaných 2075 metrov. Nadmorská výška pozorovateľa v Bratislave sa môže pohybovať od 126 m.n.m. pri Čunove po 514 m.n.m. na Devínskej Kobyle. Pre náš prípad môžeme počítať s približnou nadmorskou výškou 140 metrov. Využitím odvodeného vzťahu pre trojuholník a kružnicu dostávame vzdialenosť, pri ktorej dochádza k vzájomnej viditeľnosti oboch bodov (pozorovateľ v Bratislave, objekt v Alpách) takmer 205 km. Vyzerá to tak, že som v našom spore ťahal za kratší koniec. Nemôžeme však robiť ukvapené závery, pretože ak chceme daný vrch naozaj vidieť (predpokladajme, že geometrické podmienky georeliéfu medzi Bratislavou a Schneebergom nám to dovoľujú), nestačí vidieť len najvyšší bod, ale samozrejme aj istú časť kopca - pri pozmenení vstupných hodnôt tak, aby aspoň tretina zasneženého vrchu trčala nad obzorom, počítač vracia maximálnu vzdialenosť 155 km. Čím viac chceme vidieť, tým viac sa blížime k teoretickej hranici. A tým viac parametrov musíme brať do úvahy pri zvážení, kto v našom spore ťahal za kratší koniec.
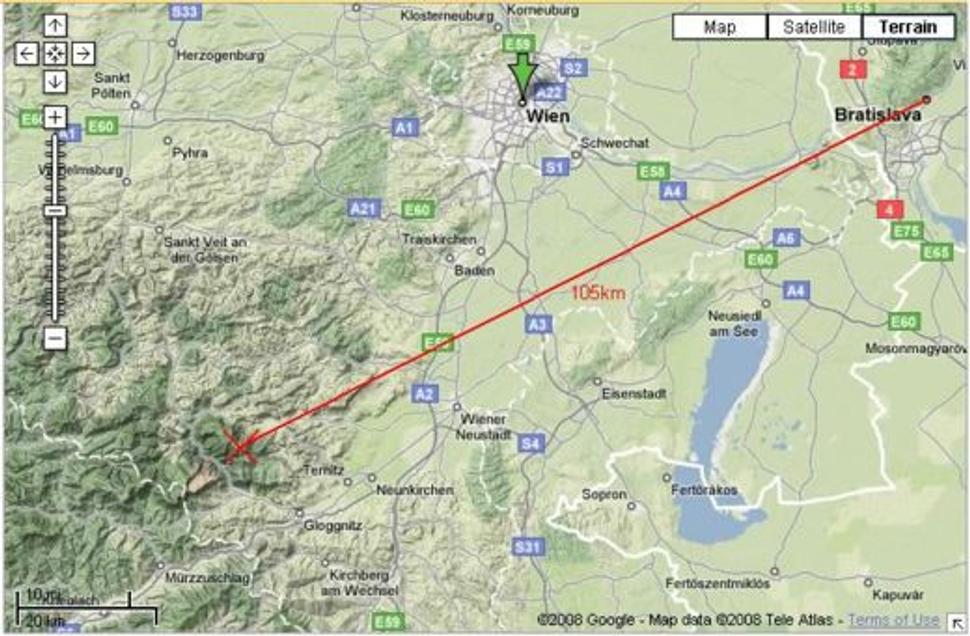
Krížikom je označená poloha Schneebergu, pohľadu z Bratislavy, zdá sa, nič nestojí v ceste.
Na jednej strane stoja nerovnosti telesa Zeme ako planéty, zmena stredného polomeru môže spôsobiť výchylky vo výsledkoch, ale odhadujem ich len na zlomky kilometra, najviac na pár kilometrov. Samozrejmosťou je aj nerovnosť už spomínaného georeliéfu lokálnej oblasti medzi Bratislavou a prvými horami Álp. Ako však vidíme z priloženej mapy, táto oblasť je "našťastie" preklenutá podunajskou nížinou. Žiadne vyššie prekážky by pohľadu nemali stáť v ceste. V prospech možnej viditeľnosti hovoria aj ďalšie dva fakty:
Za prvé sneh má mimoriadne vysoké albedo (odrazivosť svetla) a je preto vidieť doslova na míle - svieti ako maják oproti relatívne tmavému pozadiu modrej oblohy, či lesov v popredí.
Za druhé, vo svojich úvahách som doteraz neuvažoval efekt atmosférickej refrakcie, ktorý v astronómii spôsobuje "vyťahovanie" hviezd spod horizontu na oblohu. Efekt má na úrovni obzoru hodnotu čosi vyše pol stupňa, čo je zhodou okolností zdanlivý priemer Slnka a Mesiaca na oblohe. Preto keď vidíte Slnko alebo Mesiac, ako sa dotýkajú horizontu pri západe či východe, telesá už v skutočnosti zapadli a vidíte ich vďaka refrakcii - teda lomu svetla na rozhraní redších (chladnejších) a hustejších (teplejších) vrstiev atmosféry. Keďže v reálnej atmosfére samozrejme žiadne "rozhrania" spravidla nie sú, nejde ani tak o zalomenie lúčov svetla ako o ich ohnutie. Pri zvažovaní nášho prípadu viditeľnosti hôr aj takpovediac "do zákruty" sa však výsledok koriguje s tzv. terestrickou refrakciou, ktorej hodnoty sú menšie ako u astronomickej (lúč svetla neletí z kozmického priestoru a nezačne sa ohýbať už vo veľkých výškach ale omnoho nižšie - pri Schneebergu vo výške 2075 metrov). Vďaka tomuto javu, ktorého mechanizmus je inak sám o sebe mimoriadne zaujímavý, sa hory v Alpách môžu pre pozorovateľa v Bratislave zdanlivo predĺžiť a zviditeľniť.
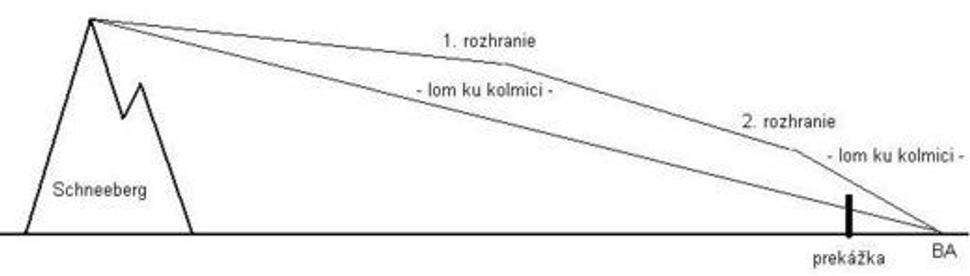
Vďaka refrakcii vidíme aj za prekážku v ceste priamemu lúču. Na obrázku je reálna refrakcia modelovaná lomom ku kolmici na dvoch tlakových rozhraniach. Tiež je značne preexponovaná, v skutočnosti ide o veľmi malé uhly. Povrch Zeme je vynesený ako rovná priamka, jeho zakrivenie simuluje prekážka.
Bez toho, aby som výpočty a úvahy ďalej komplikoval refrakciou môžeme zhrnúť, že prvé vrcholky Álp z Bratislavy musí byť vidno. Teoreticky bez diskusie, výpočet pre teleso tvaru gule je nespochybniteľný. A prakticky zrejme tiež áno - za veľmi dobrého počasia, pokrytí vrcholov hôr snehom a využitím efektu refrakcie. Týmto uznávam svoju prehru v našej rodinnej diskusii, otec naozaj mohol Alpy z Bratislavy vidieť, nech to znie akokoľvek neuveriteľne. Keďže je to teoreticky a, zdá sa, že aj prakticky možné, nemám dôvod o jeho pozorovaní ďalej pochybovať.
Už teraz sa teším, ako zasnežené Alpy z Bratislavy niekedy sám uvidím.
Pozn.: Rovnica pre vzdialenosť ideálneho horizontu je L = Rz*arccos(Rz/Rz+h) (pre uhol vyjadrený v radiánoch, Rz je polomer Zeme, h výška).






