Zázračné násobenie jedenástimi
Potrebujete vynásobiť dvojciferné číslo jedenástimi. Ako na to? Spočítajte cifry to násobeného čísla a výsledok umiestnite medzi číslice pôvodného čísla.
72x11
7+2=9 Výsledok 792
A čo ak je súčet väčší ako desať? Prevyšujúcu jednotku pridajte k prvému číslu a inak to ostáva.
87x11
8+7=15 výsledok 957
Umocnenie čísla končiaceho päťkou na druhú
Ďalší nádherný trik pre fajnšmekrov. Oddeľte od čísla poslednú číslicu. Takto získané predné číslo vynásobte číslom o jedno vyšším. Za tento súčin dopíšte 25.
452
4x(4+1)=4x5=20
Výsledok: 2025
alebo
7052
70x71=70x70+70=4900+70=4970
Výsledok: 497025
Násobenie veľkých čísiel
V roku 1980 sa v Imperial College v Londýne uskutočnil pokus. Indická žena menom Shakuntala Devi dostala náhodne vybrané dve trinásťciferné čísla - 7 686 369 774 870 a 2 465 099 745 799. Ich súčin (18 947 668 177 995 426 773 730) spočítala za 28 sekúnd. Samozrejme neprezradila presne, ako to spravila, ale s najväčšou pravdepodobnosťou použila trochu obmenenú "školskú" metódu. Bežný človek pri nej už zrejme potrebuje papier, aby si tie čísla aspoň napísal, písať však medzivýsledky je zbytočné, zvládnete to aj bez toho. Základ je napísať si dve čísla pod seba. Kedysi ma v škole pri násobení učili, že vedľa seba (zrejme kvôli šetreniu papiera), tu je to však vyslovene nevhodné.
2 684 513
x 9 245 416
Celkovo sa výpočet bude skladať z trinástich krokov tak, že spárujeme čísla podľa čiar a vynásobíme ich medzi sebou a tieto medzivýsledky sčítame. Čo ostane nad desiatku presunieme do ďalšieho kroku. 1. krok:
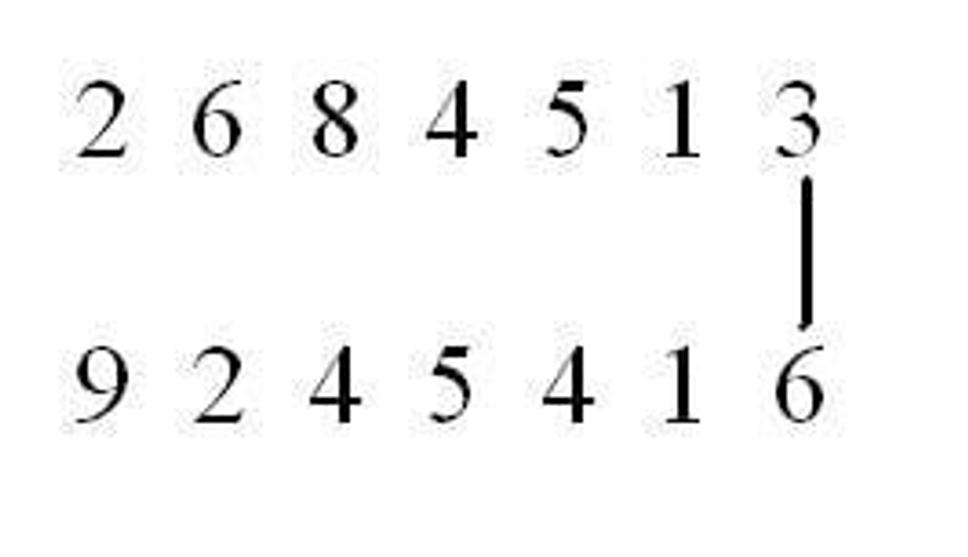
3x6 = 1 8
2. krok:
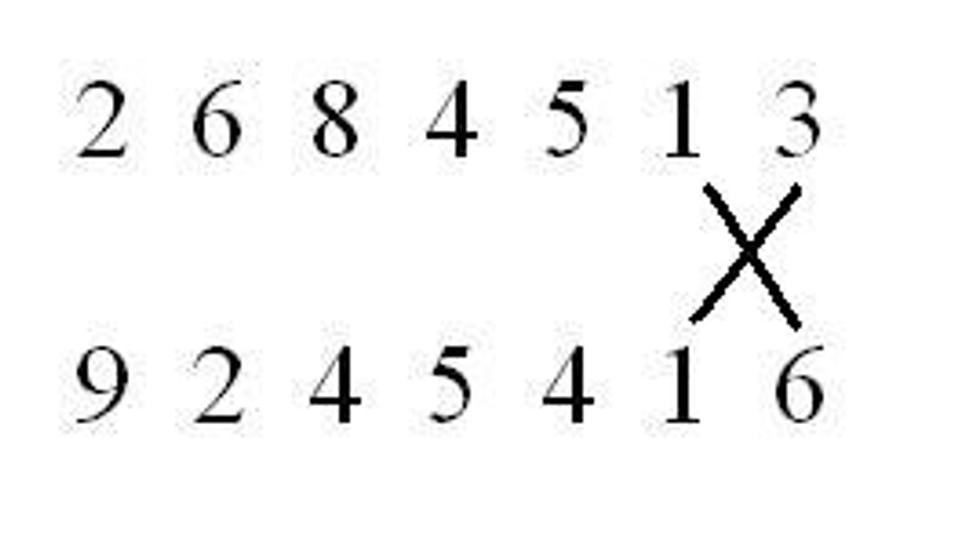
1+6x1+1x3=1+6+3=1
3.krok:
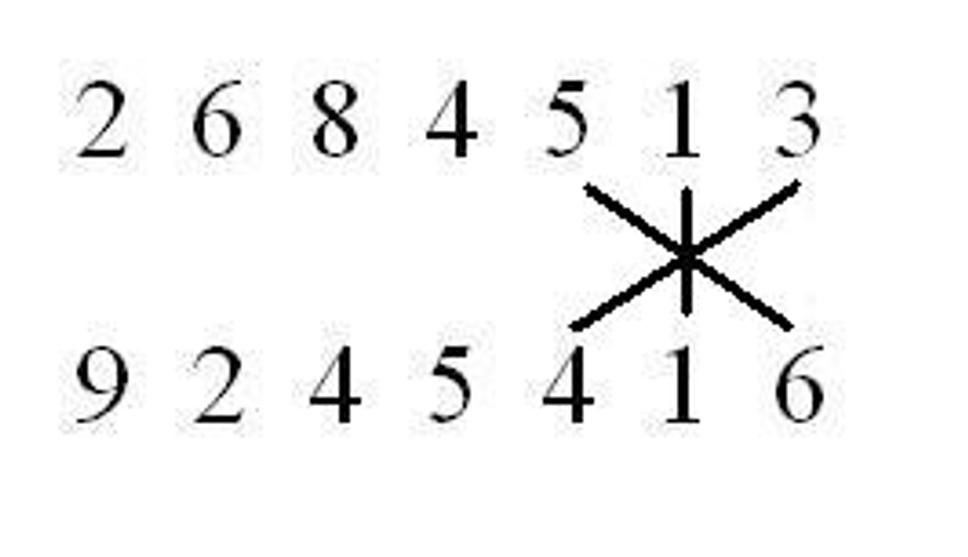
1+6x5+1x1+4x3=1+30+1+12=4 4
analogicky potom ďalšie kroky:
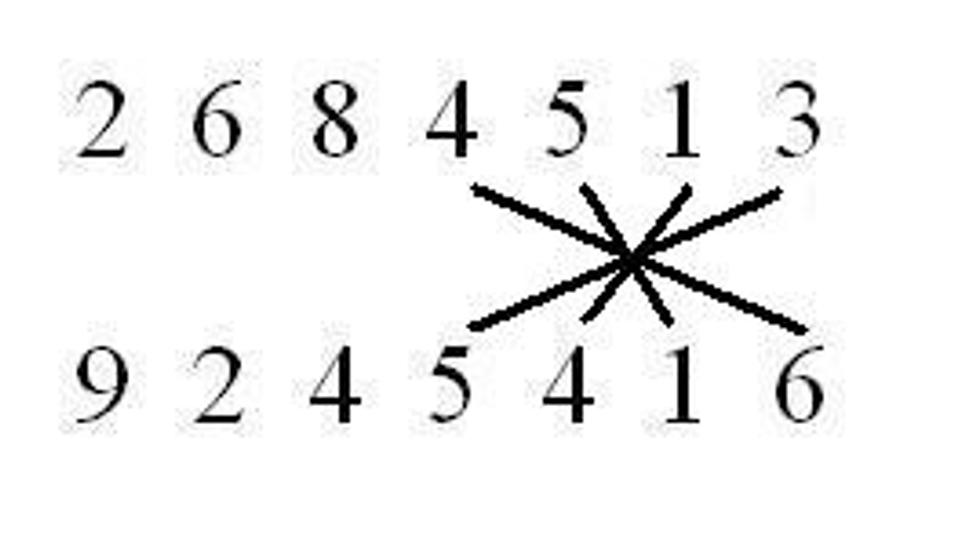
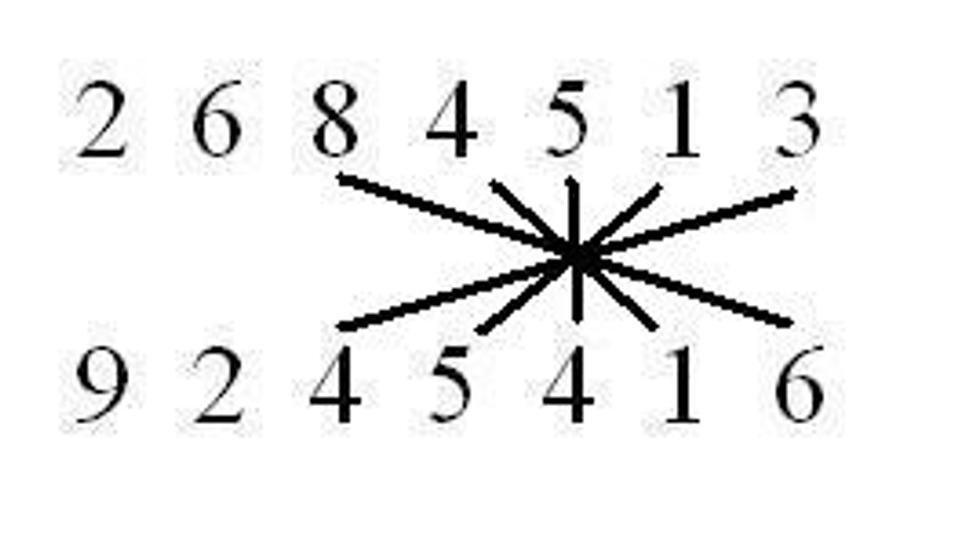
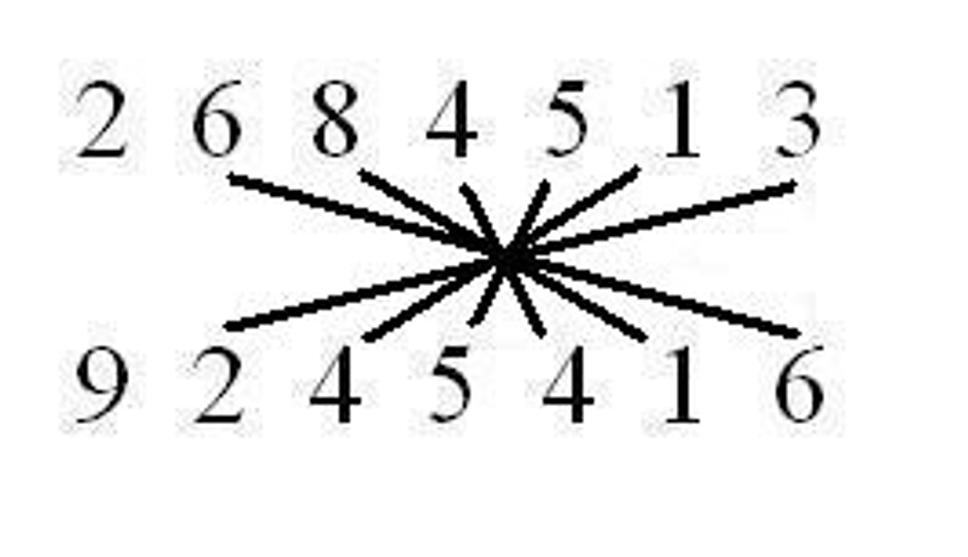
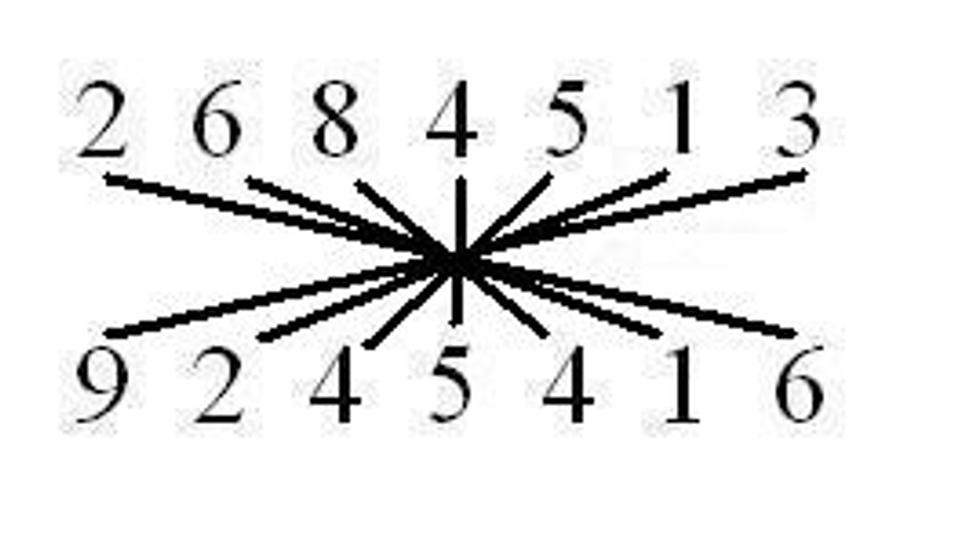
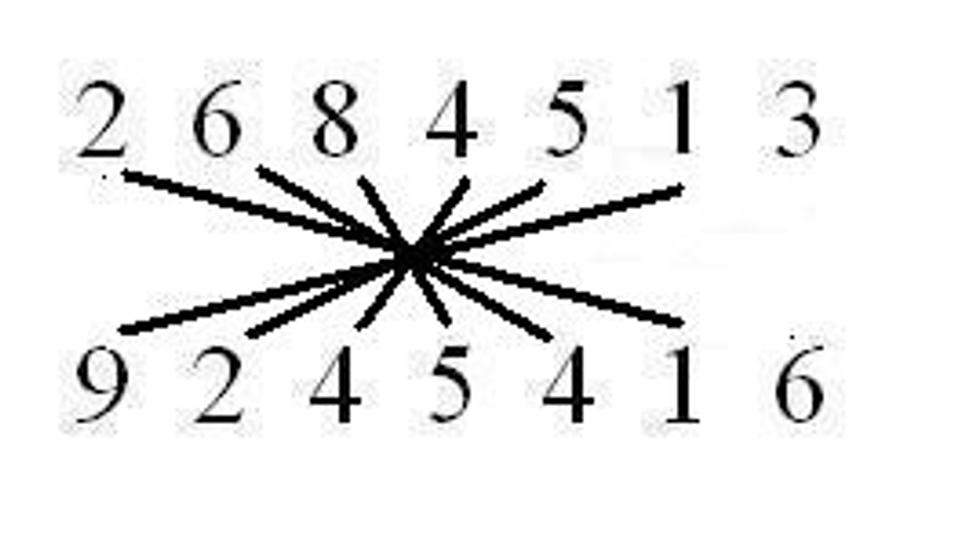
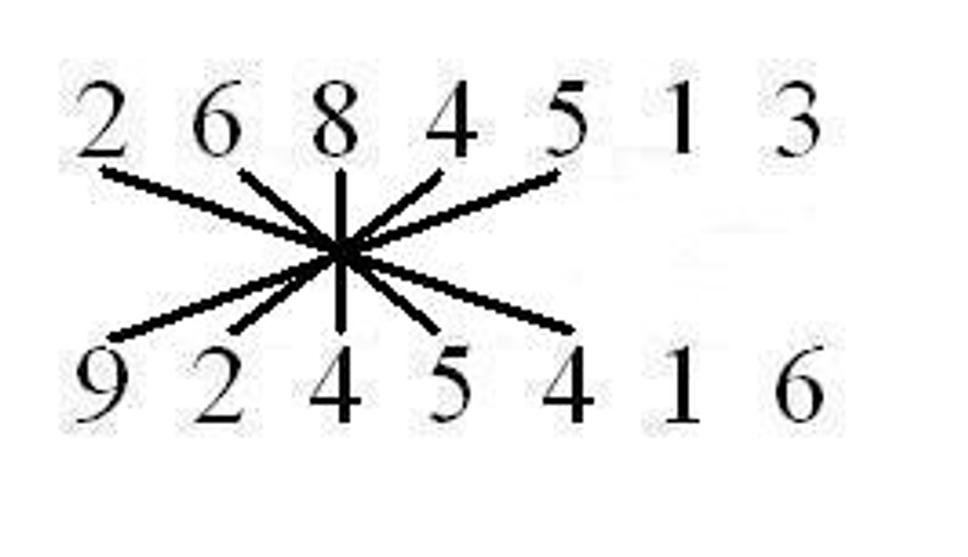
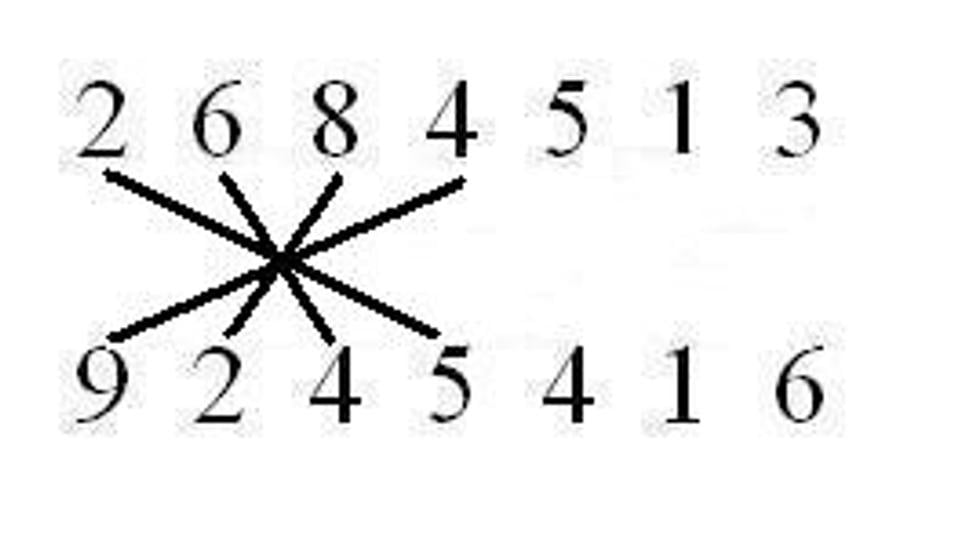

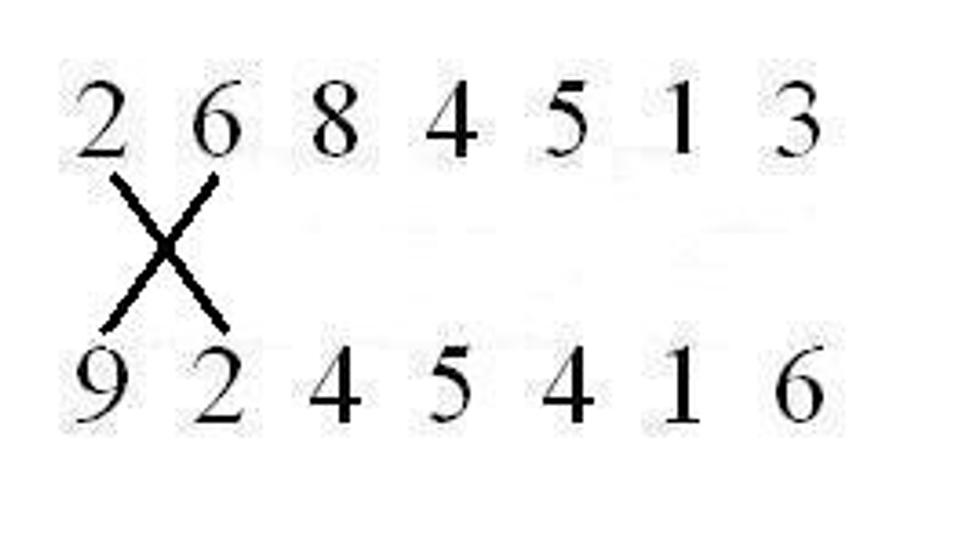
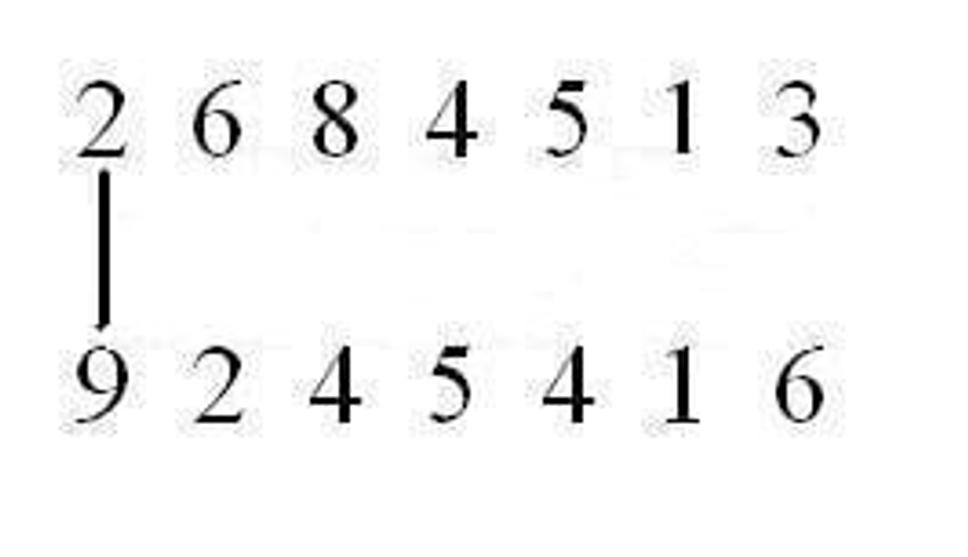
Keď by sme teraz mali papier, odzadu napíšeme výsledok 24 819 439 442 408. Teraz sa vrátime k tej indickej počtárke. Pri násobení dvoch trinásťciferných čísel musela vykonať 169 násobení a 167 sčítaní. To je 336 matematických operácií za 28 sekúnd, čiže viac ako 12 za sekundu alebo jednu za 8 stotín sekundy. A to sme ešte nezarátali čas potrebný na napísanie výsledku, čo bolo 26-ciferné číslo, ktorého zapísanie tiež niečo trvá. Že to nebola iba náhoda, ale schopnosti Indky, dokazuje aj to, že v roku 1977 zhlavy vypočítala dvadsiatutretiu odmocninu zo 101 ciferného čísla.
Tretia odmocnina za okamih
Toto nemá pre bežného človeka žiadne praktické využitie. Ale skúste to spraviť len tak, pomimo, ako budú všetci hľadieť. Vyzvite niekoho, nech si zvolí dvojciferné číslo, na kalkulačke ho umocní na tretiu a výsledok vám povie (napríklad 110592). A vy mu hneď poviete pôvodné číslo. Najskôr si ale pozrite nasledujúcu tabuľku:
13 = 1
23 = 8
33 = 27
43 = 64
53 = 125
63 = 216
73 = 343
83 = 512
93 = 729
103 = 1000
Akonáhle vám dotyčný povie výsledok, odmyslite si posledné tri čísla (ostalo nám 110) a zvyšok v hlave porovnajte s číslami v tabuľke. Dostanete prvú číslicu (v našom prípade 4, lebo 110 je medzi 64 a 125). Potom si pozrite poslednú číslicu výsledku - ak si všimnete, tak v tabuľke je každá posledná číslica iná. Podľa nej zistíte druhú číslicu hľadaného čísla (110592 končí na dvojku - rovnako ako 512, čo je osem na tretiu - takže hľadaný výsledok je 48). Čiže sa stačí naučiť tabuľku naspamäť a pôvodné číslo viete skôr, než stihnete na cudzej kalkulačke nájsť, ako tretiu odmocninu vôbec počíta.
Trik s dátumom narodenia
Vyzvite priateľa, nech napíše na papier mesiac svojho narodenia, ale nech vám to neukazuje. (Január - 1, február - 2 atd., pre náš príklad, narodil sa v novembri 1969 - napíše 11). Nech toto číslo zdvojnásobí (22), pridá päť (27) a následne vynásobí päťdesiatimi (1350). Teraz nech k takto získanému číslu pridá svoj vek (1350+39=1389). Teraz ho ešte vyzvite nech odpočíta 365 a výsledok vám povie (1024).
Vy teraz už iba rýchlo pripočítate 115 a dostanete 1139 - a keď si toto číslo rozdelíte v mysli na prvé dve číslice a druhé dve, hneď viete povedať, že sa narodil v jedenástom mesiaci a má 39 rokov.
Pri tomto triku si musíte dať pozor na jedno úskalie, totiž aby priateľ nebol starší ako 115 rokov, inak vám to bude vychádzať vždy.
Trik s chýbajúcou číslicou
Vyberte si dobrovoľníka a povedzte mu, nech si ľubovoľne zvolí také trojciferné číslo, aby najväčšiu číslicu mal prvú, strednú druhú a najmenšiu ako tretiu (napríklad 843). Potom mu povedzte, aby toto číslo obrátil a potom obrátené číslo od pôvodného odpočítal (843 - 348 = 495). Ďalej mu povedzte, aby aj tento výsledok obrátil, ale pre zmenu tieto dve čísla sčítal (495 + 594 = 1089). Teraz mu môžete po chvíľke predstieraného rozmýšľania povedať výsledok - 1089.
Než sa stihne obeť spamätať z vášho kúzla, vyzvite ju, nech ho prenásobí ľubovoľným trojciferným číslom a povie vám koľko cifier má výsledok (napríklad 1089 x 658 = 716562, povie vám, že šesť). Potom ju vyzvite, aby povedala v ľubovoľnom poradí číslice výsledku, ale jednu nech si nechá pre seba. (Povie vám trebárs 5,6,1,6,2). A vtedy sa zamyslíte mu poviete chýbajúcu číslicu (7).
Tajomstvo kúzla je vcelku jednoduché. Ak dodržíte podmienky, 1089 vám v prvej časti výjde vždy. Preto to na jednej osobe moc neopakujte, lebo jej to príde hneď podozrivé, že vychádza rovnaký výsledok. Číslo 1089 je deliteľné deviatimi, keď ho prenásobíte hociakým trojciferným číslom, výsledok ostane deliteľný deviatimi. Ako si možno spomeniete zo školy, tak číslo je deliteľné deviatimi, pokiaľ jeho ciferný súčet je deliteľný deviatimi. Takže ak si tie číslice, ktoré vám povie, sčítate, tak musíte pridať takú číslicu, aby súčet bol deliteľný deviatimi (v našom príklade máme 5+6+1+6+2=20, do najbližšieho násobku deviatky, ktorým je 27, nám chýba 7 - to je číslica, ktorú nám obeť nepovedala). Jeden háčik nastane, ak súčet cifier je práve deliteľný deviatimi. Vtedy totiž chýbajúcou číslicou môže byž aj 0 aj 9. Vtedy treba trochu zablafovať. Položte napríklad otázku: Nenechal si si nulu pre seba? A podľa jeho reakcie už zistíte, či bude prekvapený, alebo pokýve hlavou, že nie. Potom už iba sucho skonštatujete, že ani jednotku, dvojku ani trojku, ale presne deviatku zatajil.
Takže zázračným matematikom zdar! :)






