Trochu na precvičenie mozgu alebo ako využiť matematiku

Úloha 1:

Uvediem dva výroky a z nich zostavím záver. Otázka znie, či je záver logicky správny, či vyplýva z daných viet.

1: Bank of Northern Ireland nemá učet v Bank of England.
2: Finančná kríza nespôsobila Bank of Northern Ireland žiadnu stratu.
Záver: Existuje aspoň jedna banka, ktorá nemá účet v Bank of England a finančná kríza jej nespôsobila stratu.

Úloha 2:

1. Po meste jazdí 90 čiernych taxíkov a 10 tmavomodrých.
2. V noci za dažďa zrazil jeden taxík chodca a z miesta nehody ušiel.
3. Svedok tvrdil, ze to bol tmavomodrý taxík.
4.Policajti svedka za podobných poveternostných podmienok na rovnakommieste neskôr preskúšali a na dostatočne veľkom množstve pokusovzistili, že v štyroch prípadoch z piatich stanovil farbu taxíka správne.
Otázka: Čo je na základe viet 1-4 pravdepodobnejšie? Že chodca zrazil tmavomodrý alebo čierny taxík?

Úloha 3:

Aký je najmenší počet závaží, ktorými sa dá na dvojramenných váhach na jedno váženie navážiť ľubovoľné celočíselné množstvo kilogramov od 1 do 40?

Úloha 4:

Istý druh vodnej rastliny za jedeň deň zdvojnásobí svoj počet listov, pričom všetky listy majú rovnakú veľkosť. Ak do rybníka nasadím 1 list, za 30 dní bude celá hladina pokrytá listami. Za koľko dní bude hladina pokrytá listami, ak nasadím dva listy?

Úloha 5:

Vzájomný spor sa páni Anton, Boris a Cyril rozhodli vyriešiť pištolami. Strieľať sa bude dovtedy, kým zostane nažive len jeden. Anton je najhorší strelec, do terča sa trafí v jednom pokuse z troch. Boris je lepší, cieľ trafí z troch rán dvakrát. Cyril je ostrostrelec a trafí sa vždy. Aby bol ten súboj spravodlivejší, začne Anton, potom bude strieľať Boris (ak bude ešte žiť) a po ňom Cyril a tak to pôjde dokola, až kým neostane len jeden. Kam má zamieriť Anton svoju prvú ranu?

Úloha 6:

Na futbalovom ihrisku sa pohybujú hráči oboch tímov a rozhodca, dohromady 23 ľudí. Išli by ste do stávky 1:1 so mnou, ak by som vám tvrdil, že na ihrisku sa nachádzajú dvaja ľudia, ktorí oslavujú narodeniny v rovnaký deň? Úloha 1:

Záver je chybný. Oba výroky (1,2) sú pravdivé, napriek tomu ten záver z nich nevyplýva. Figeľ je v tom, že žiadna Bank of Northern Ireland neexistuje, ten názov som si vymyslel. Je síce možné, že výrok je pravdivý (že by ste banku spĺňajúcu podmienky záveru našli), ale nemá to žiadnu súvislosť s predchádzajúcimi dvoma vetami. Len som chcel poukázať na to, že akékoľvek "samozrejmé" uvažovanie, vôbec nemusí dávať správne výsledky.

Ak by ste dali túto úlohu Aristotelovi, ktorý rozpracoval základy logického uvažovania, odpovedal by na ňu, podľa záverov v jeho dielach chybne. Ľudstvu trvalo viac ako 2000 rokov, než prišlo na to, že sa mýlil.

Úloha 2:

Keď v štyroch z piatich určil správne a povedal, že to bol tmavomodrý, tak si zrejme drvivá väčšina z vás pomyslí, že je pravdepodobnejšie, že taxík bol tmavomodrý.
Teraz si to trochu rozmeňme na drobné. Ak by sme prebrali všetky možné prípady, tak z 90 čiernych áut by svedok klasifikoval 18 ako modré (90/5=18) a zvyšných 72 ako čierne. Z 10 modrých taxíkov by 8 správne označil za modré a 2 za čierne. Ak teda povedal, že videl modrý taxík, tak to bol buď jeden z tých 8 skutočne modrých alebo jeden z tých osemnástich zdanlivo modrých (čiže v skutočnosti čierny). Teraz je už zrejmé, že na základe známych údajov to bol skôr čierny taxík (na 69,2%) ako tmavomodrý.

Ak sa vám to riešenie aj tak zdá trochu čudné, pozrite sa na to z opačnej strany. Keby nebolo svedka, bola by pravdepodobnosť modrého taxíka 10% (10 zo sto). Výpoveďou svedka sa pravdepodobnosť modrého taxíka zvýšila na 30%. Bohužiaľ, svedectvo nebolo dostatočne preukazné, aby sa z neho dali robiť jednoznačné závery. Za zmienku stojí, že ak by svedok určil čierne taxi, tak by pravdepodobnosť čierneho taxi stúpla z 90% na 97,3% (Bol by to jeden zo 72 skutočne čiernych, alebo dvoch zle označených modrých).

Toto je záludný príklad na rozoznanie tzv. pravdepodobností a priori a a posteriori. A priori je pravdepodobnosť udalosti tak, ako je daná ešte predtým, než sa dozvieme súvisiacu informáciu. Práve tento fakt podstatnou mierou znížil výpovednú hodnotu svedka. Riešenie takéhoto typu problémov priniesol Thomas Bayes v druhej polovici osemnásteho storočia.

Úloha 3:

Tu by asi málokto neprišiel na možnosť mať závažia 1,2,4,8,16 a 32 kilové. Keď sa ale spomínajú dvojramenné váhy, nič nám nebráni pokladať závažia na obe strany, teda aj k váženému tovaru. To potom umožňuje vynechať dvojkilové a dať rovno trojkilogramové - veď dva kilogramy navážime tak, že na jednu misku dáme tri kilá a na druhú kilo plus dve kilá tovaru. Potom si vystačíme so štyrmi závažiami: 1,3,9 a 27, čo sa dá ľahko dokázať , keď si to na papieri vyskúšate (1=1;2=3-1;3=3;4=3+1;5=9-3-1;6=9-3;7=9+1-3;8=9-1;9=9;10=9+1;11=9+3-1 atd.)

Túto úlohu publikoval Claude Gaspar Bachet de Mézirac začiatkom sedemnásteho storočia v knihe Problèmes plaisants et délectables qui se font par les nombres.

Úloha 4:

Pokiaľ za jeden deň z jedného listu narastú dva o rovnakej veľkosti ako pôvodný, tak pokiaľ nasadíme dva listy hneď prvý deň, bude to rovnaká situácia ako na druhý deň potom, čo sme nasadili jeden. Čiže ušetríme jeden deň, takže celý rybník sa zaplní rastlinou za 30 - 1 = 29 dní.

Neviem, kto vymyslel túto úlohu, ale raz som ju dostal asi ako šiestak na nejakej matematickej súťaži a ja somár som napísal, že za 15 dní. Podstatné je si uvedomiť, že tu sa nejedná o štruktúru priamej úmernosti, ktorá je v bežnom živote nesmierne rozšírená, ale o štruktúru geometrickej postupnosti, ktorá sa správa inak.

Úloha 5:

Pozrime sa, aké má Anton možnosti. Môže zamieriť na Borisa. Pokiaľ trafí, na rade bude Cyril, ktorý určite trafí, čiže Anton je dopredu mrtvý.
Teraz trochu pozor, čo sa stane, keď netrafí. Na rade bude Boris. Nepochybne bude mieriť na nebezpečnejšieho súpera - Cyrila (Ak by mieril na Adama a trafil, tak ho Cyril ďašou ranou odstrelí). Pokiaľ ho trafí na rade bude Anton a jeho súperom už iba Boris. Ak Boris Cyrila netrafí, bude Cyril určite cieliť naspäť na Borisa, lebo je nebezpečnejší a skolí ho. Na rade bude Anton a za súpera bude mať Cyrila. Či už Boris Cyrila zabije alebo nie, v konečnom dôsledku bude mať Anton ďalšiu ranu a už iba jedného súpera.
Ďalšou možnosťou je mieriť na Cyrila. Ak ho trafí, na rade bude Boris a za súpera bude mať iba Antona. Ten sa bude musieť spoliehať, že ho Boris netrafí a on jeho ďalšou ranou áno.
Pokiaľ Anton Cyrila netrafí, bude rovnaká situácia, akoby mieril na Borisa a netrafil a to je už popísané vyššie.
Teraz už každý vidí, že pre Antona je najvýhodnejšou možnosťou, keď netrafí. Horšie je, keď trafí Cyrila. Pokiaľ ale prvou ranou skolí Borisa, je naisto vo večných loviskách. Preto bude najlepšie, keď Anton namieri - do vzduchu. Boris s Cyrilom budú strieľať po sebe a jemu ostane jeden rival a jedna rana, ktorou na 33% prežije.

Úloha 6:

Pre zjednodušenie vynechajme 29.2., t.j. deň, ktorý má nižšiu pravdepodobnosť výskytu ako ostatné.
Zdalo by sa, že keď ľudí je len 23 a dní v roku 365, tak by som bol asi blázon, keď by som sa chcel staviť. Zase si to ale rozmeňme na drobné.
Každý človek sa môže narodiť v jednom z 365 dní, takže celkový počet rôznych možností narodenia tých ľudí je 365.365.365...365. 365 s tým, že tých činiteľov je tam 23, t.j. 365²³.
A teraz si úlohu obráťme na to, koľko je možností, že sa v ten istý deň nenarodili. Prvý sa môže narodiť v jednom z 365 dní, druhý už iba v jednom z 364 dní (jeden deň je už obsadený), ďalší v 363 atd. až posledný v 365-22=343. Čiže kombinácií rôznych dátumov narodenia je 365.364.363....344.343.
Teraz už len stačí zistiť, akú veľkú časť zo všetkých možností tvoria kombinácie, že sa v rovnakom dni nenarodili.

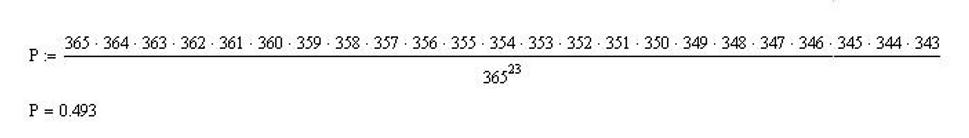
Čiže pravdepodobnosť, že sa narodili v rôzne dni je 49,3%, takže ak tvrdím, že nájdem dvoch, ktorí sa v rovnaký deň narodili na 50,7% vyhrám. Ak by som takúto stávku robil dlhodobo, určite by som bol v pluse.
Otázkou je, prečo sa nám to zdá ťažko uveriteľné, veď tých ľudí tam na trávniku nie je tak veľa. Zdôvodnenie by bolo zrejme v tom, že by sme sa nemali pozerať na to, koľko je tam ľudí, ale koľko rôznych dvojíc možno z tých ľudí zostaviť. Ak je ich tam 23, môžeme skombinovať 253 rozličných párov, ktoré môžu mať rovnaký deň narodenia. Ak by ste sa stavili na vianočnom večierku s tridsiatimi ľuďmi, párov by bolo 435 a vaša šanca na výhru by prekračovala 70%.

A teraz čo som tým šaškárením chcel povedať. Isto mi na základe riešení dáte za pravdu, že každú z týchto úloh možno vypočítať matematickým aparátom, ktorý sám osebe nie je veľmi zložitý. Problémom je, že hoci teóriu by sme všetci zvládli, chýba nám správna myšlienka, ako si z kvanta vedomostí získaných v našom školskom systéme, vybrať tie, ktoré použiť a akým spôsobom ich spojiť, aby sme dostali želaný výsledok. Presne to, čo sa neustále na našom školstve kritizuje a neustále sa s tým nič nerobí.
Napríklad úlohu 6, by naše učebnice riešili pravdepodobne tak, že by uviedli vzorec:

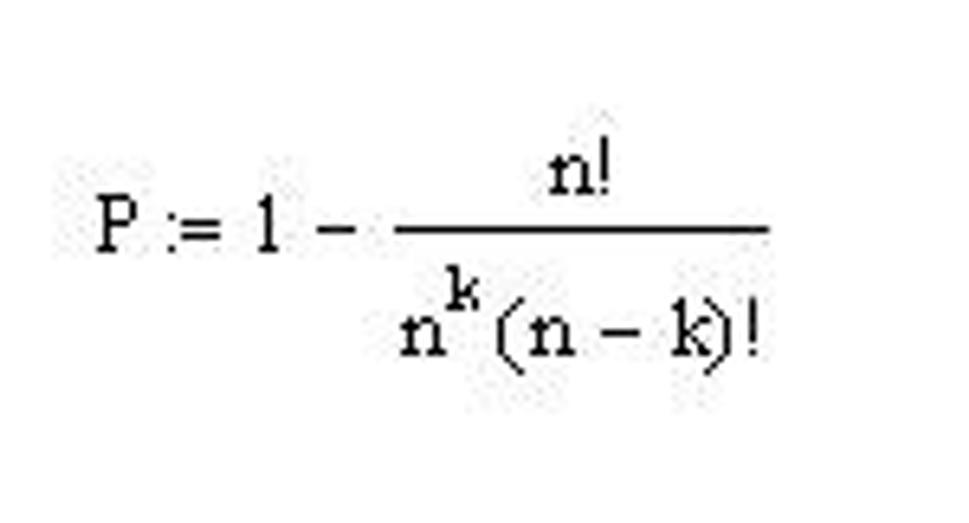
a nech si žiak dosadí za k číslo 23 a za n číslo 365. (Teraz odhliadnem od faktora, že bežná kalkulačka by mu to nevypočítala) Nič viac a učebnica, odvodená od slova učiť, by pokračovala ďalším príkladom.

Nespochybňujem, že pre vysokú matematiku je nutné používať symbolické zápisy, bežný človek ale takú matematiku vo svojom živote nepotrebuje. Na to, aby pochopil situáciu príkladu 5 si ho nemusí prekladať do reči matematiky, čo by znelo približne nasledovne: Máme bezkoaličnú hru 3 hráčov v normálnom tvare. Pre každého hráča i ε {1,2,3} je daná množina stratégií S_i a reálna funkcia V_i definovaná na karteziánskom súčine S₁xS₂xS₃ nazývaná výplatnou funkciou atd. V momente by sme boli všetci nahraní a netušili by sme, že ide o akčnú strielačku a nevyriešili by sme absolútne nič.

Zo všetkých predmetov má práve matematika najväčší potenciál rozvíjať samostatné myslenie, keď sa však zmení na biflovanie vzorcov typu
sin(2x) = 2. sin (x). cos (x)
a nekonečné upravovanie výrazov s nejakými ixami, ypsilonmi a podobne, tak mi neostáva povedať nič iné, iba že sa tento potenciál preflákava. Ako by to išlo inač a praktickejšie, sa snažil ukázať tento článok.

Ak ste aspoň jednu úlohu vyriešili sami, gratulujem, ste lepší ako ja. Doplnené 31.12.2008

Iné riešenie úlohy 6 (bez veľkých čísiel):

najskôr oslovíme prvého človeka. Pravdepodobnosť, že sa nenarodil v rovnaký deň ako niekto iný je zatiaľ 1,0 (100%), lebo ho nemáme s kým porovnávať. Potom oslovíme druhého. Tento sa už mohol narodiť iba v jednom zo 364 dní, lebo jeden dátum už je obsadený prvým človekom. Pravdepodobnosť, že sa narodil v iný deň ako predchádzajúci človek je 364/365 = 0,9973. Potom preskúmame tretieho. Jeho pravdepodobnosť, že sa narodil v iný deň ako tí pred ním je 363/365. Postupne napíšeme tabuľku, kde v druhom stĺpci bude pravdepodobnosť, že sa nenarodil v rovnaký dátum ako tí pred ním.

Nás ale nezaujíma prípad každého konkrétneho futbalistu, nás trápi, aká je pravdepodobnosť, že sa v rovnaký deň ako ostatní, narodil každý. Za jeden jav chápeme, že sa niekto narodil v taký dátum ako nikto pred ním. Dátum narodenia každého jedného sú nezávislé javy, preto výslednú pravdepodobnosť dostaneme ako súčin pravdepodobností jednotlivých javov - musí byť splnené, aby sa druhý nenarodil rovnako ako prvý, tretí, ako prví dvaja atd. Výsledok je potom súčin čísiel z druhého stĺpca a to je 0,4927 t.j. 49,27%. Pravdepodobnosť, že stávku vyhrám je teda približne 50,3%.

Literatúra:

Keith Devlin, The Language of Mathematics: Making the Invisible Visible, ISBN 0805072543
Simon Singh, Fermat´s Last Theorem, ISBN 9781841157917
Tibor Šalát a kol., Malá encyklopédia matematiky, Obzor, 1978