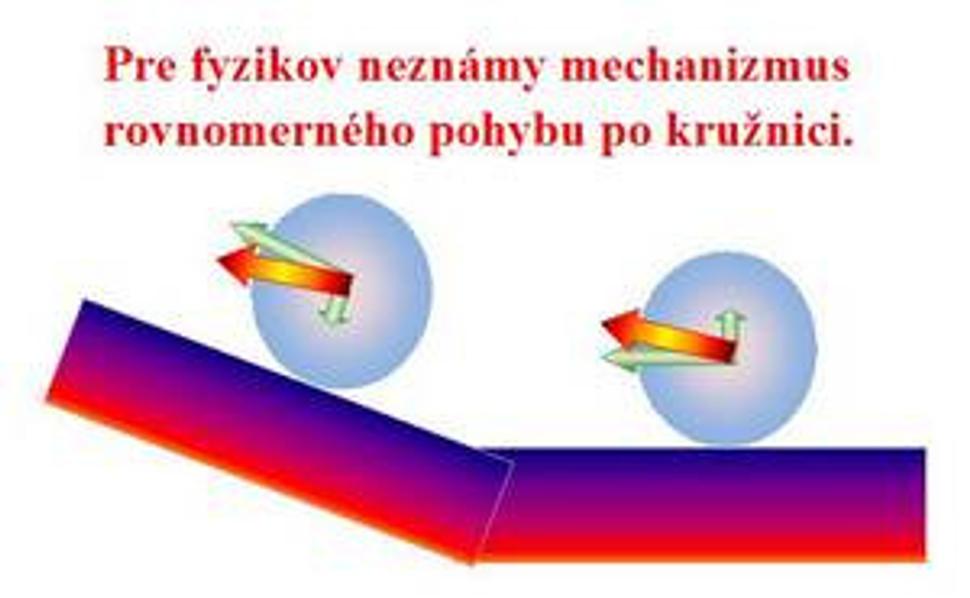
Reálny a preto absolútne pravdivý fyzikálny mechanizmus zmeny smeru vektora rýchlosti pri rovnomernom pohybe telesa po kružnici.
Podľa súčasnej, relativistickej fyziky, existuje v prírode taká (Newtonom zadefinovaná) silová interakcia, ktorá nemení veľkosť vektora rýchlosti, ale mení iba jeho smer.
Konkrétnym príkladom toho má byť rovnomerný pohyb telesa po kružnici , pri ktorom sa veľkosť vektora rýchlosti nemení , (teleso má stálu, konštantnú rýchlosť) ale zato sa vraj neustále mení smer predmetného vektora rovnomerného pohybu.
Tento fyzikálny paradox (ľudovo povedané táto fyzikálna hovädina ) sa dá opísať výlučne diferenciálnou matematikou , ktorá je tiež stelesnením matematického paradoxu (ľudovo povedané matematickou hovädinou ) konštatujúceho jednotu nula rozmernej dimenzie s jednorozmernou dimenziou, pomocou zjednocujúceho, super hovädinového matematického aparátu zvaného limita postupnosti (samozrejme iba matematických, teda abstraktných, myšliemkových, s materiálnou prírodou neharmonizujúcich) čísel .
Aby sranda bola dokonlá, je potrebné uviesť aj to, že pojem limity postupnosti a s ňou spojený diferenciálny počet nevymyslel nikto iný, ako Izák Newton autor uvedenej fyzikálnej hovädin y.
Takže relativistická fyzika , spolu s diferenciálnou matematikou dospeli k nasledovnému paradxnému záveru, že na teleso pohybujúce sa rovnomernou rýchlosťou po kružnici, pôsobí na dráhe dx , presnejšie na nulovej dráhe, za čas dt , presnejšie za nulový čas , nenulové dostredivé zrýchlenie o veľkosti a = v2 /R. a = (dx2 /dt2 )/R
To, že tento opis rovnomerného pohybu po kružnici je výplod matematicko - fyzikálnych dementov, alebo ľudí s malou kapacitou reálneho myslenia, dokazuje nasledovný JÁRAYov opis reálneho fyzikálneho mechanizmu zmeny smeru vektora rýchlosti pri rovnomernom pohybe telesa po kružnici.
Obraz č. 1.
Teleso ktorého veľkosť zotrvačného pohybu v sústave prezentuje iba jeden výsledný vektor , pri náraze do pevnej, nepoddajnej prekážky, rozdelí sa na jeho dva sprievodné vektory a to na vektor normálový (kolmý na nepoddajnú prekážku) a na vektor tangenciálny , (teda rovnobežný z plochou prekážky)
Obraz č. 2.
Experimentálne teleso po dotyku s pevnou a nepoddajnou prekážkou, začne sa pružne deformovať vo smere normálového vektora , teda v smere kolmom na prekážku, pričom sa normálový vektor rýchlosti zmenšuje, následkom jeho prerodu z kinetickej hodnoty na hodnotu potenciálnu.
( Táto pružná deformácia prebieha následkom tzv. zotrvačnej odstredivej sily. )
Tým pádom aj veľkosť výsledného vektora rýchlosti pohybu telesa sa zmenšuje , ale súčasne aj rotuje smerom k jeho tangenciálnej vektorovej zložky.
Veľkosť výsledného vektora pohybu telesa sa počas jeho deformácie neustále zmenšuje a súčasne aj rotuje !!!
Ako je to znázornené na obraze č. 2.
Obraz č. 3.
Pružná deformácia experimentálneho telesa sa ukončí v momente, keď sa celá kinetická energia normálového vektora, premení na potenciálnu energiu , čiže, keď normálový kinetický vektor zanikne .
Následkom zániku normálového vektora rýchlosti telesa, jeho pôvodne výsledný vektor rýchlosti dorotuje do polohy tangenciálneho vektora, ktorého tým pádom nahradí.
V tomto momente deformácie telesa, teleso má už iba jedinú rýchlosť a to najmenšiu, čiže iba rýchlosť tangenciálnu.
Táto realita je znázornená na obraze č. 3.
Obraz č. 4.
Po skončení fáze pružnej normálovej deformácie telesa, nastanú v telese štrukturálne zmeny (s ktorými sa nemienim tu zaoberať) následkom čoho sa potenciálny, normálový vektor začne premieňať na vektor kinetický , na vektor zrýchľujúci , ktorý ale začne pôsobiť v opačnom smere , teda dostredivo.
Tak v materiálnej prírode vzniká dostredivé zrýchlenie , ktoré s hodnotou:
a = v2 /R. a = (dx2 /dt2 )/R
a s diferenciálnou matematikou, nemá nič spoločného .
Veľkosť takto vznikajúceho normálového vektora dostredivého zrýchlenia , mení nielen veľkosť výsledného vektora rýchlosti telesa, ale aj jeho smer, čiže prispieva k jeho ďalšej rotácii.
Táto realita je znázornená na obraze č. 4.
Obraz č. 5.
Keď sa celá potenciálna energia normálového vektora premení na kinetickú energiu dostredivého normálového vektora rýchlosti , ukonči sa aj pružná deformácia experimentálneho telesa a tým sa ukončí aj rotácia jeho výsledného vektora zotrvačného pohybu , s tým, že výsledný vektor pohybu nadobudne svoj pôvodný rozmer , ale už bode smerovať do celkom iného smeru, než smeroval pred vstupom do procesu pružnej deformácie telesa s nepoddajnou prekážkou.
Táto realita je znázornená na obraze č. 5.
Obraz č. 6.
Tu opísaný fyzikálny mechanizmus zmeny smeru vektora rýchlosti pri zdanlivom rovnomernom pohybe telesa po kružnici, je pretransformovaný na zdanlivo rovnomerný pohyb telesa po kružnici na obraze č. 6.
aaaaaaaaaaaa
Záverečné konštatovanie:
Teleso pohybujúce sa po kružnici nikdy nekoná rovnomerný pohyb , to preto, že jeho vektor rýchlosti sa neustále mení a pri tom aj rotuje.
K zmene smeru vektora pohybu telesa, k jeho rotácii , nemôže dochádzať bez zmeny veľkosti jeho rýchlosti.
Bez zmeny jeho rýchlosti.
Bez zmeny jeho rýchlosti.
Bez zmeny jeho rýchlosti.
K zmene smeru vektora telesa, pohybujúceho rovnomerne po kružnici, nie je potrebná dostredivá sila ani diferenciálna matematika.
To všetko preto, že žiadne teleso nie je schopné konať žiadný druh pohybu po kružnici.
Preto ani rovnomerný pohyb po kružnici.
( Geniálne geniálna JÁRAYova veta .)
To preto, lebo matematicky poňatá kružnica v materiálnom časopriestore neexistuje , to je iba matematikmi vymyslená, metafyzická, abstraktná konštrukcia.
Teleso pohybujúce sa zdanlivo po kružnici, podlieha naraz dvom úplne rôznym silovým interakciám, ktoré Newton zhrnul do jedinej silovej interakcii, čiže do ekvivalentnej silovej interakcii a to v jeho tretiom zákone Akcii a reakcii.
1. Vo vzťahu k nepoddajnej prekážke teleso podlieha zákonu akcie a reakcie .
Prekážka v každom momente odoláva normálovej, kolmej sile (ktorá vyvoláva pružnú deformáciu telesa), rovnako veľkou, ale opačne orientovanou silou.
Ide o nekauzálnu silovú interakciu .
2. Teleso vo vzťahu k jeho vnútornej štruktúre, podlieha úplne inéj, teda kauzálnej silovvej interakcii , v ktorej normálova zotrvačná hmotnosť telesa je väčšia, ako pružný, potenciálny odpor, prezentujúci pevnosť telesa.
Dokonalú pružnosť vykazuje každý atóm chemického prvku, z ktorých sa skladajú vešetky materiálne telesa, pohybujúce sa po domnelej kružnici, domnelým rovnomerným pohybom.
(Preto musí existovať aj fyzika pružných atómov, na ktorú neplatia zákony neatómovej fyziky (napríklad zákony elmag. polí).
No a túto podvojnú silovú interakciu pružných atómov chemických prvkov, mozog relatívne vzdelaných fyzikov, nie je schopný pochopiť a tak oni aj naďalej hlásajú totálne bludy o existencii nezrýchľujúcej dostredivej sily , pri rovnomernom pohybe telesa po kružnici, ktorá by mala mať veľkosť:
a = v2 /R,
ale ktorá ju nemá !!
Všetko je úplne inakšie.
Diskusia je možná na nasledovnej adrese:






