Začnem jednou anekdotou. Na otázku rodičov, čo sa naučil na prvej hodine náboženstva, odpovedal žiačik takto: "Na počiatku nebolo nič. Potom Boh stvoril svetlo. Naďalej nebolo nič, ale bolo to lepšie vidieť...". Nuž a môj blog si v duchu odpovede žiačika posvieti na to "nič", pretože sa bude venovať štúdiu geometrie tzv. prázdnych vesmírov, tj. takých, v ktorých sa nenachádza žiadna hmota. Dôvod študovať tieto prázdne vesmíry pritom nie je čisto akademický. Ak totiž v tom pravdivom našom vesmíre nie je tej hmoty priveľa, bude sa jeho geometria ponášať na geometriu toho "prázdneho nič".
Zdôrazním, že pod pojmom vesmír nechápu fyzici nejaký objekt, ktorý sa vyvíja v čase, ale chápu vesmír ako množinu všetkých udalostí, ktoré pánbožko stvoril, jedná sa pritom o udalosti presne priestorovo a časovo vymedzené v intuitívnom zmysle týchto slov, napr. udalosťou je, keď sa lopta odrazí od spojnice brvna a žrde a pod. Plynutie času je súčasťou popisu vesmíru a mimo vesmíru čas jednoducho neexistuje. Einstein zistil, že na vesmíre ako množine udalostí existuje istá geometria, tj. môžeme napríklad určovať vzdialenosť dvoch blízkych udalostí, zoskupovať udalosti do čiar i obrazcov, merať uhly medzi pretínajúcimi sa čiarami a pod. Dotyčnej geometrii sa hovorí gravitačné pole. Nie každá matematicky predstaviteľná geometria je fyzikálne realizovateľná, tie realizovateľné sa vyznačujú tým, že riešia tzv. Einsteinove rovnice. Keď sa vo vesmíre pohybuje kus hmoty, tak ovplyvňuje tvar Einsteinových rovníc a teda i fyzikálne realizovateľné geometrie. Zaujímavý fakt je ten, že Einsteinove rovnice umožňujú riešenia vo forme netriviálnych fyzikálne realizovateľných geometrií, aj keď je vesmír prázdny a žiadny kus hmoty sa v ňom nenachádza. Mnohé takéto "prázdne" riešenia sa napr. interpretujú ako tzv. gravitačné vlny. Ak pridáme požiadavku, aby riešenie Einsteinových rovníc vyzeralo čo najsymetrickejšie, tak síce eliminujeme gravitačné vlny, ale i tak dostaneme tri netriviálne alternatívy so značne odlišnou geometriou, ktorým sa hovorí de Sitterov, anti de Sitterov a Minkowského vesmír. Špeciálne tieto tri geometrie sa líšia správaním v nekonečne, kde štvorrozmerný de Sitter vyzerá ako trojrozmerný priestor bez času, štvorrozmerný anti de Sitter tam vyzerá ako trojrozmerný obyčajný priestoročas a štvorrozmerný Minkowski tam vyzerá ešte čudesnejšie tj. ako trojrozmerný svetelne degenerovaný priestoročas. Experimentálne dáta naznačujú, že vesmír, v ktorom žijeme, sa najviac ponáša na ten de Sitterov, ale budeme podrobne študovať všetky tri alternatívy, keďže Minkowského vesmír zodpovedá Einsteinovej špeciálnej teórii relativity a geometria nekonečna anti de Sitterovho vesmíru ja zasa kľúčová pre štúdium tzv. holografie.
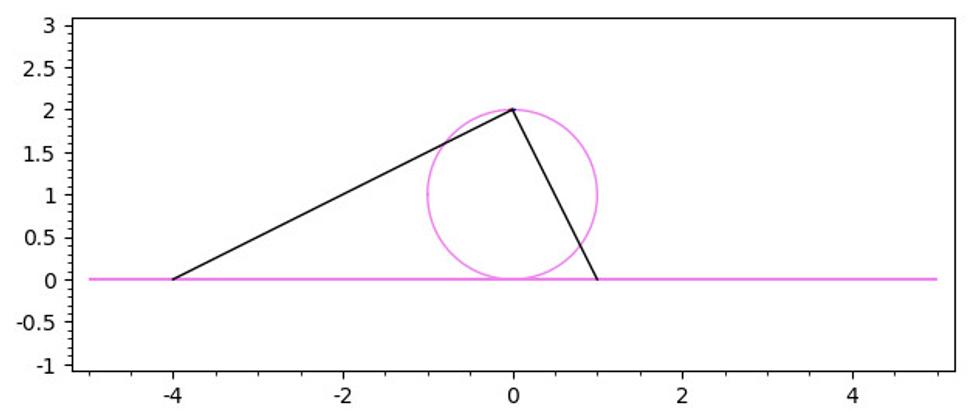
Podobne ako skokani na lyžiach robia prvé kroky-skoky na malých mostíkoch, my začneme výklad na vesmíroch malých rozmerov. Napr. obyčajná priamka je jednorozmerný vesmír, pretože na určenie polohy bodu na priamke postačuje určenie jediného čísla, tzv. súradnice bodu. Máme tu dve možnosti, buď tento vesmír znázorňuje čistý priestor, kde čas vôbec neplynie ako v rozprávke o Šípkovej Ruženke, alebo naopak znázorňuje čistý čas, keď jednorozmerný vesmír obsahuje jediné tikajúce hodiny (tj. udalosti sú tiky týchto hodín). Predstavme si teraz, že sa chceme dozvedieť, ako tento vesmír vyzerá v nekonečne. Za týmto účelom ho zavinieme do kružnice, alebo, použijúc, odborný jazyk, do projektívnej kvadriky typu (1,2). Urobíme to ako na Obr.1. a zistíme, že ak utekáme po priamke do nekonečna či už smerom doprava alebo doľava, z pohľadu zavinutého vesmíru sa v obidvoch prípadoch približujeme najvyššiemu bodu kružnice, ktorému preto hovoríme bod v nekonečne. Tomuto bodu v nekonečne, ktorý už do pôvodného vesmíru nepatrí, sa často hovorí konformná hranica vesmíru.
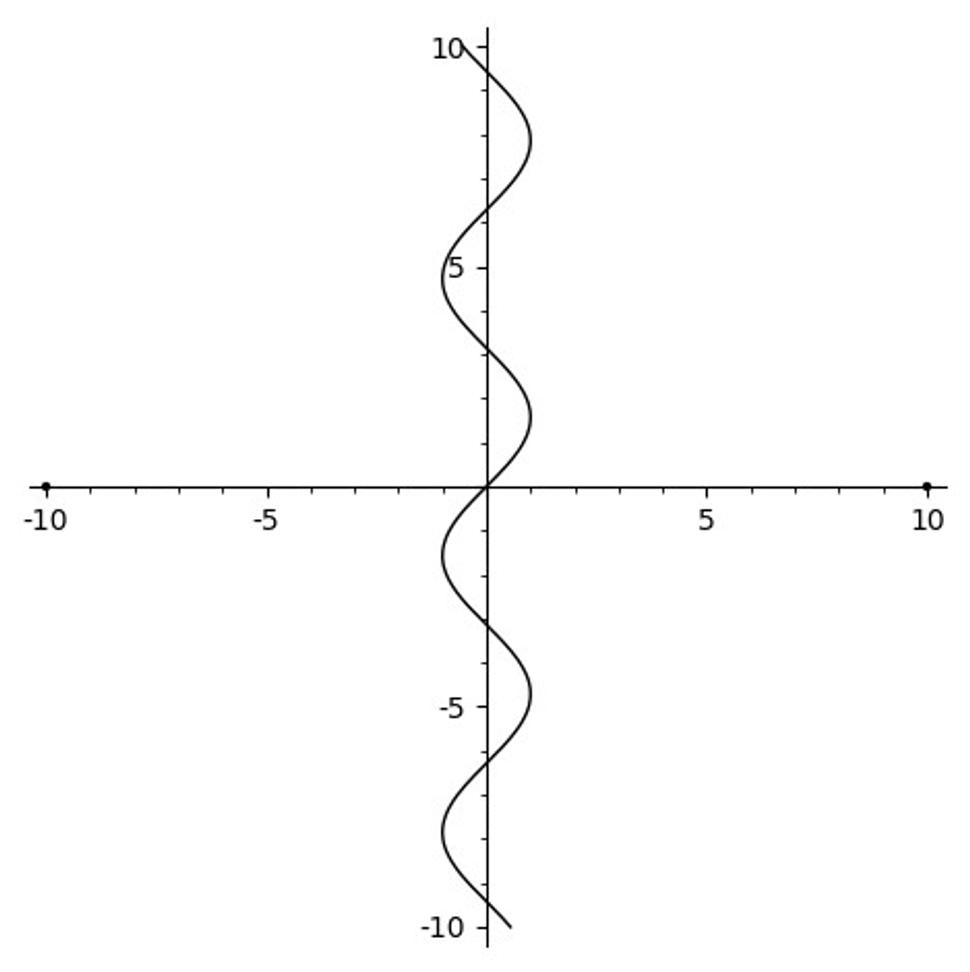
Prejdime teraz do dvoch rozmeroch, z ktorých jeden bude priestorový a druhý časový. Začnime od dvojrozmerného tzv. Minkowského vesmíru, ktorý je z geometrického hľadiska obyčajnou rovinou. V tejto rovine môžeme zakresľovať krivky vystihujúce rôzne deje odohrávajúce sa vo vesmíre, napr. môžeme popísať priebeh partie preťahovania lanom. Na obrázku 2 je vyobrazená takáto partia preťahovania, kde súťažiace družstvá sú približne rovnako silné a raz jedno a raz druhé získava malú výhodu. Poloha stredu lana na priamke v danom čase je bod vesmíru a kľukatá čiara popisuje priebeh partie.
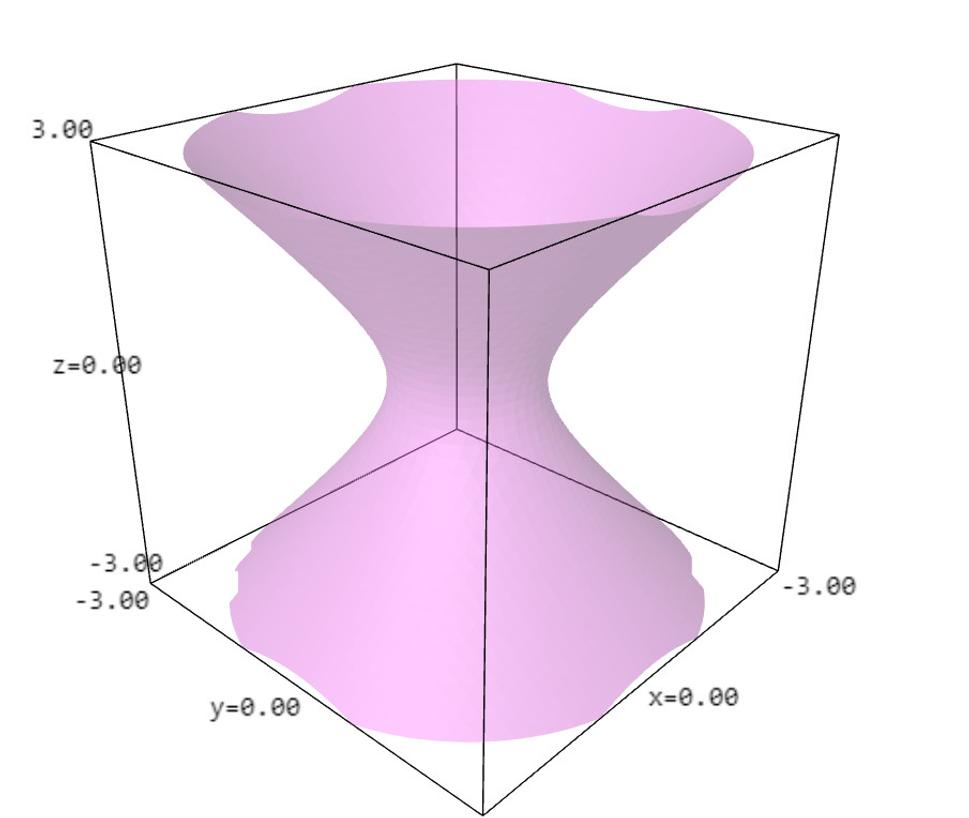
De Sitterov a anti de Sitterov vesmír v dvoch dimenziách naopak nie sú roviny, ale dajú sa znázorniť ako povrchy rotačných jednodielnych hyperboloidov v trojrozmernom priestore, viď obrázok 3.
Minkowského, de Sitterov a anti de Sitterov vesmír majú veľmi rozdielne fyzikálne vlastnosti. Kým napr. v Minkowského vesmíre si môžem posvietiť na jeho ľubovoľného iného obyvateľa, v de Sitterovom môžu existovať obyvatelia, ktorých lúč svetla z mojej baterky nikdy nedostihne. Podobne v Minkowského vesmíre "nevstúpime dvakrát do tej istej rieky", kým v anti de Sitterovom čas plynie dookola a môže sa nám to podariť (hovorí sa tomu odborne, že v anti de Sitterovom vesmíre existujú uzavreté časupodobné krivky). Naším cieľom bude nájsť, ako vyzerajú body v nekonečne toho ktorého vesmíru, alebo, inými slovami, ako vyzerá jeho konformná hranica. Asi neprekvapí, že všetky tieto tri rôzne sa správajúce nekonečné vesmíry budú mať rôzne správanie sa v nekonečne, ale čo môže prekvapiť je fakt, že keď ku každému z nich pridáme jeho konformnú hranicu dostaneme rovnaký výsledok! Inými slovami všetky tieto tri rôzne vesmíry sa dajú KONFORMNE zavinúť do toho istého konečného vesmíru! Dôraz je tu kladený na slovo konformne, ktoré označuje, že zavinutie môže meniť vzdialenosti, ale nemôže meniť uhly. Tým konečným zavinutým vesmírom je projektívna kvadrika typu (2,2), ktorá nie je ničím iným než povrchom pneumatiky ako na obrázkoch 4, 5 a 6. Na obr. 4 je naznačené, ako vyzerá priestor na konečnom zavinutom vesmíre; t.j. červenomodrý pásik označuje množinu udalostí odohrávajúcich sa v tom istom čase. Na obr. 5 je ilustrované, ako plynie na zavinutom vesmíre čas; t.j. červenomodrý pásik označuje tikanie istých konkrétnych hodín. Nakoniec na obr. 6 je ukázané, ako sa šíri na zavinutom vesmíre svetlo. Červenomodrý pásik znázorňuje pohyb fotónu v jednom smere a purpurovotyrkysový v protismere.
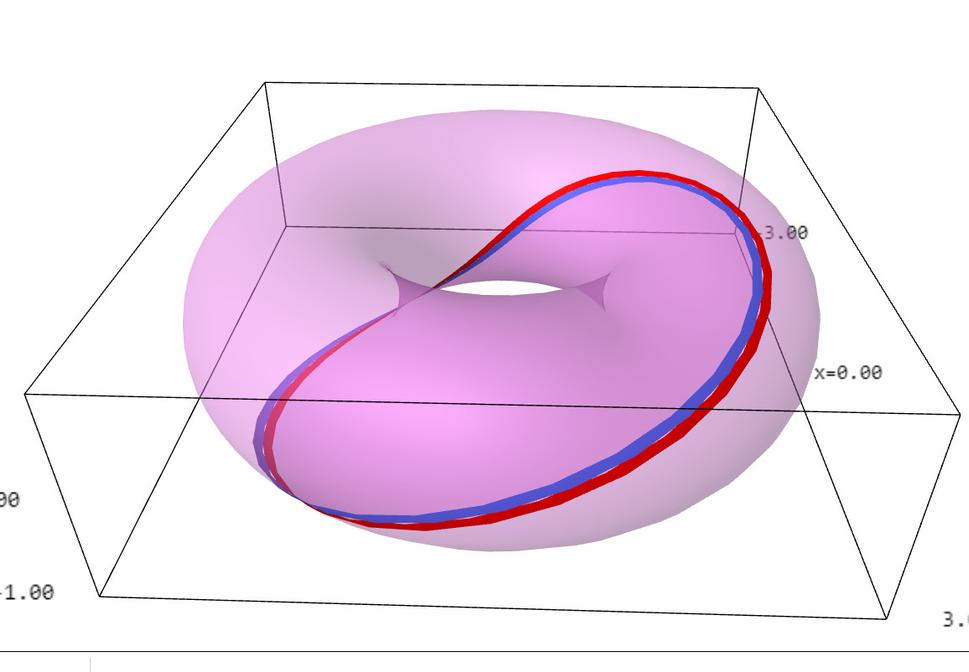
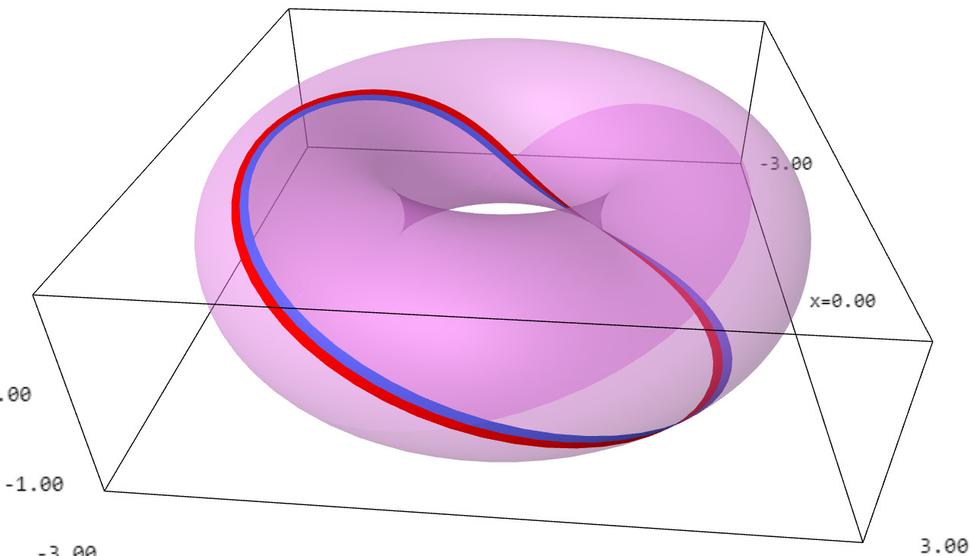
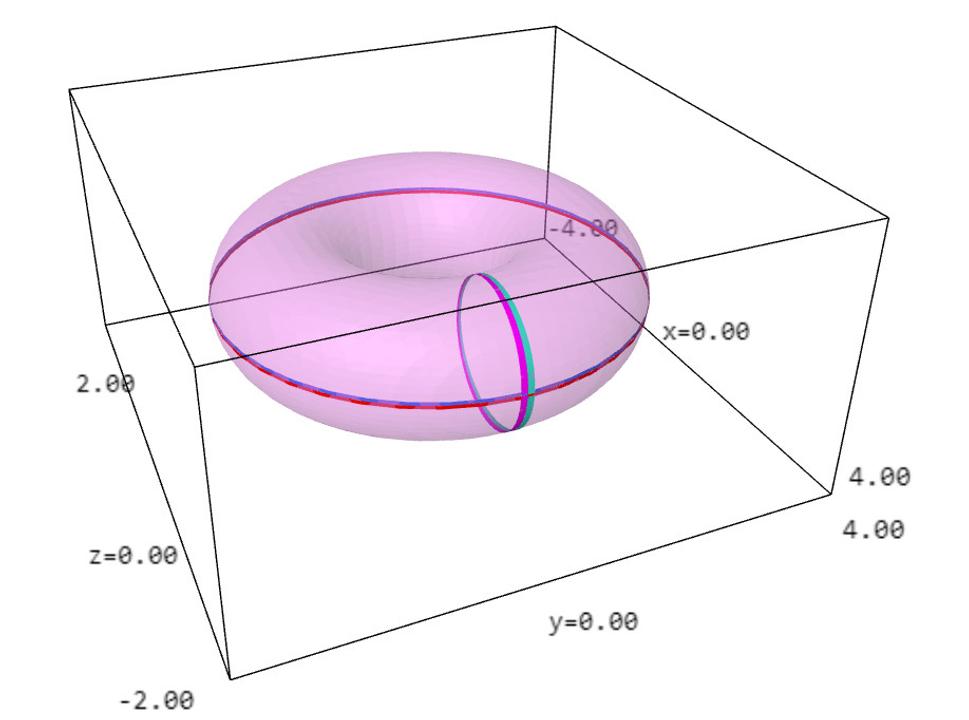
No a teraz sa ukazuje pozoruhodná vec. Ak z pneumatiky na obr. 4 vyhodíme červenomodrý pásik, dostaneme zavinutý dvojrozmerný de Sitterov vesmír (inými slovami, vyhodený pásik zodpovedá bodom, ktoré sú z hľadiska de Sitterho vesmíru v nekonečne). Ak z pneumatiky na obr. 5 vyhodíme červenomodrý pásik, dostaneme zavinutý anti de Sitterov vesmír a nakoniec ak z pneumatiky na obr. 6 vyhodíme červenomodrý i purpurovotyrkysový pásik, dostaneme zavinutý Minkowského vesmír.
Fyzici veľmi často postupujú tak, že informáciu obsiahnutú na obrázkoch 4,5 a 6 znázorňujú dvojrozmerne tým, že prerežú pneumatiku pomedzi dvoma farbami dvojfarebných pásikov a výsledok rozvinú do roviny. Takto sa získajú obrázky 7,8 a 9.
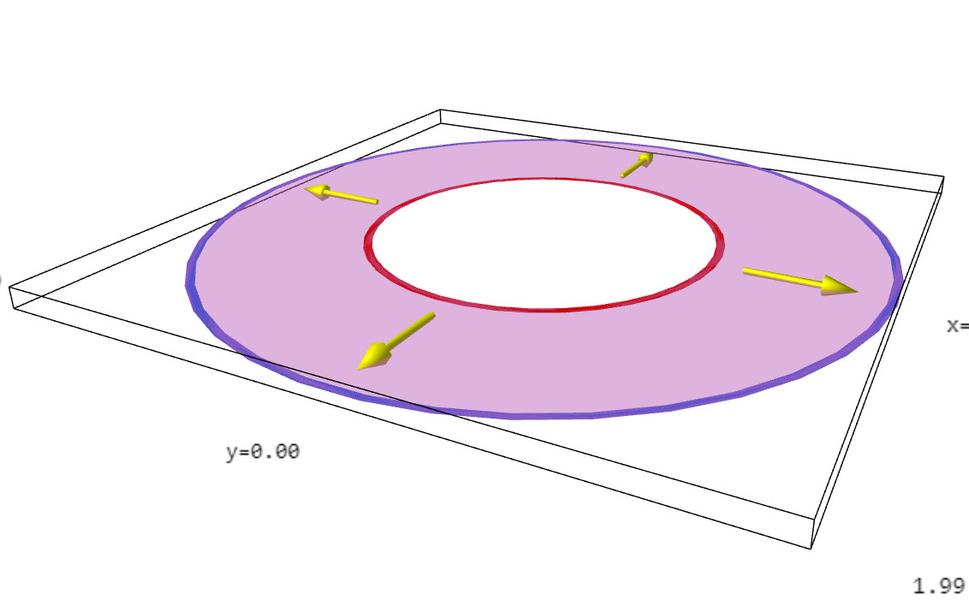
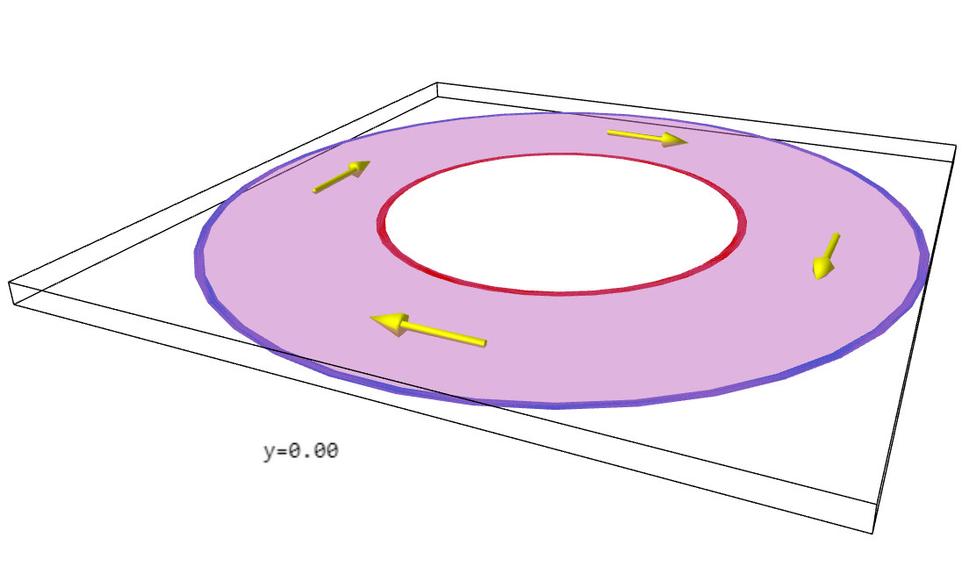
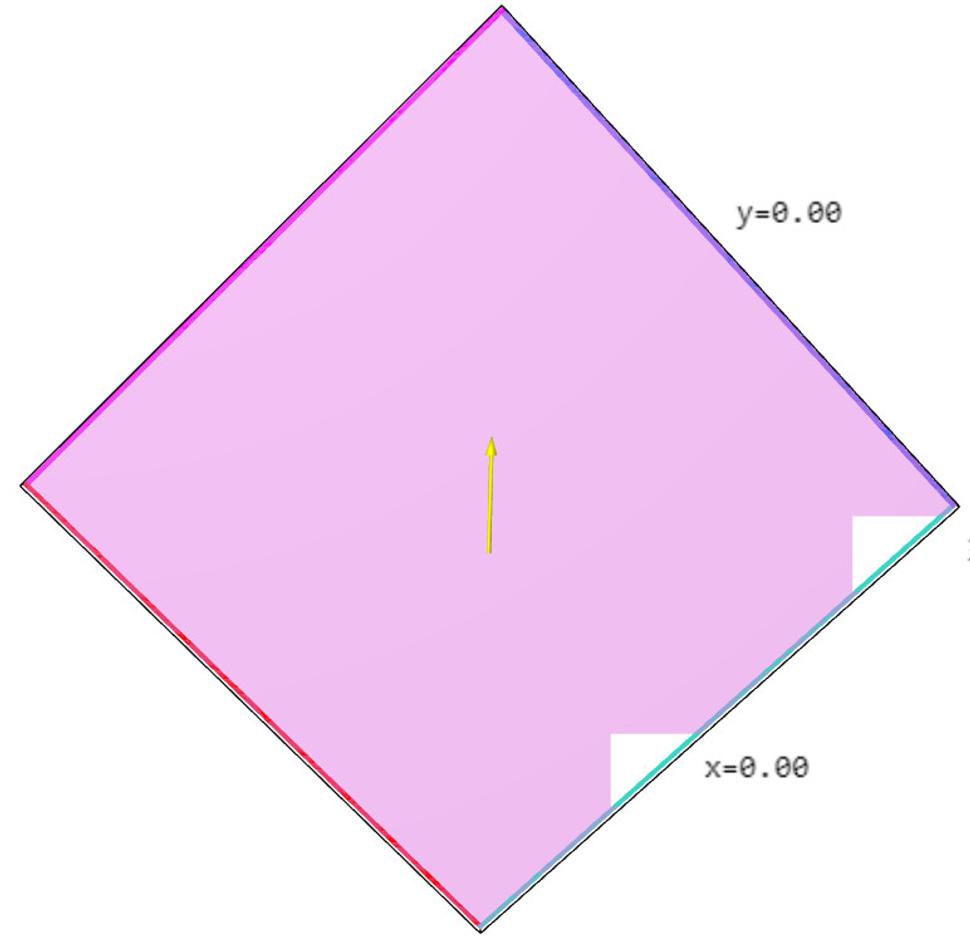
Skúmajme teraz de Sittera, anti de Sittera a Minkowského v troch rozmeroch, tj. v dvoch priestorových a jednom časovom. V Minkowského prípade máme do činenia s obyčajným trojrozmerným priestorom, v ktorom žijeme, ale de Sitter či anti de Sitter si predstaviť v globále nedokážeme. Jazyk matematiky nám síce povie, že aj de Sitter aj anti de Sitter sa dajú znázorňovať ako isté podmnožiny štvorrozmerného priestoru, ale v štyroch rozmeroch nevieme kresliť a tak nevieme namaľovať zovšeobecnenie obrázku 3 o jeden rozmer vyššie. Pokiaľ ide o štúdium konformných hraníc (tj. bodov v nekonečne), jazyk matematických rovníc nám síce prezradí, ako konformne zavinúť trojrozmerný de Sitter, anti de Sitter i Minkowski do toho istého konečného vesmíru, prezradí nám tiež, že tento konečný vesmír je projektívna kvadrika typu (3,2), prezradí nám ako vyzerá priestor i čas na tejto kvadrike, ako sa tam pohybuje svetlo atď. problém je len v tom, že si to všetko nedokážeme nakresliť! Ani obrázky typu 4,5 a 6 teda nevieme nakresliť o rozmer vyššie. Nevieme teda nakresliť nič? Našťastie vieme. Vieme nakresliť zovšeobecnenia obrázkov 7,8 a 9 o rozmer vyššie. Podobne ako sme v dvojrozmernom prípade rozrezali konečný zavinutý vesmír pozdĺž pásika a rozvinuli ho do dvojrozmernej roviny, o rozmer vyššie postupujeme podobne, tj. rozrežeme trojrozmerný konečný zavinutý vesmír pozdĺž istej dvojrozmernej dvojfarebnej plochy a rozvinieme výsledok do trojrozmerného priestoru. Dostaneme tak obrázky 10 až 16.
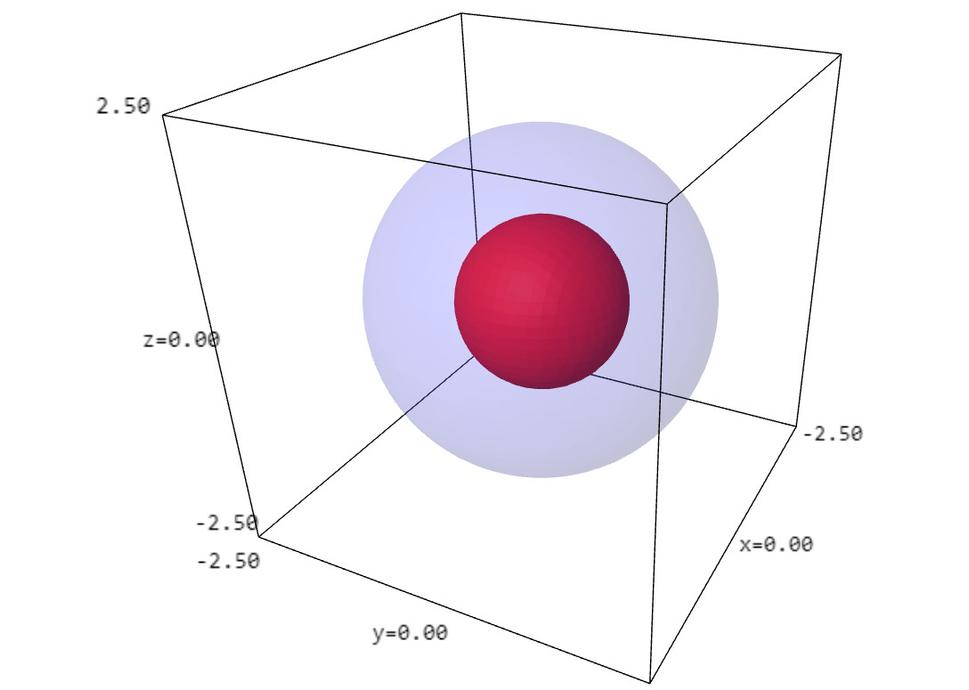
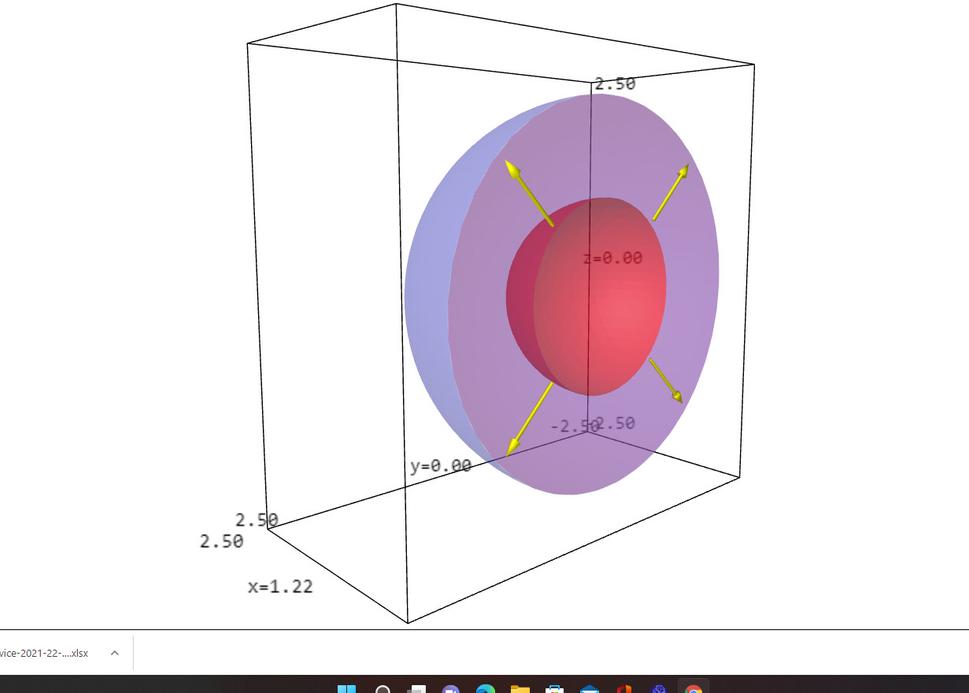
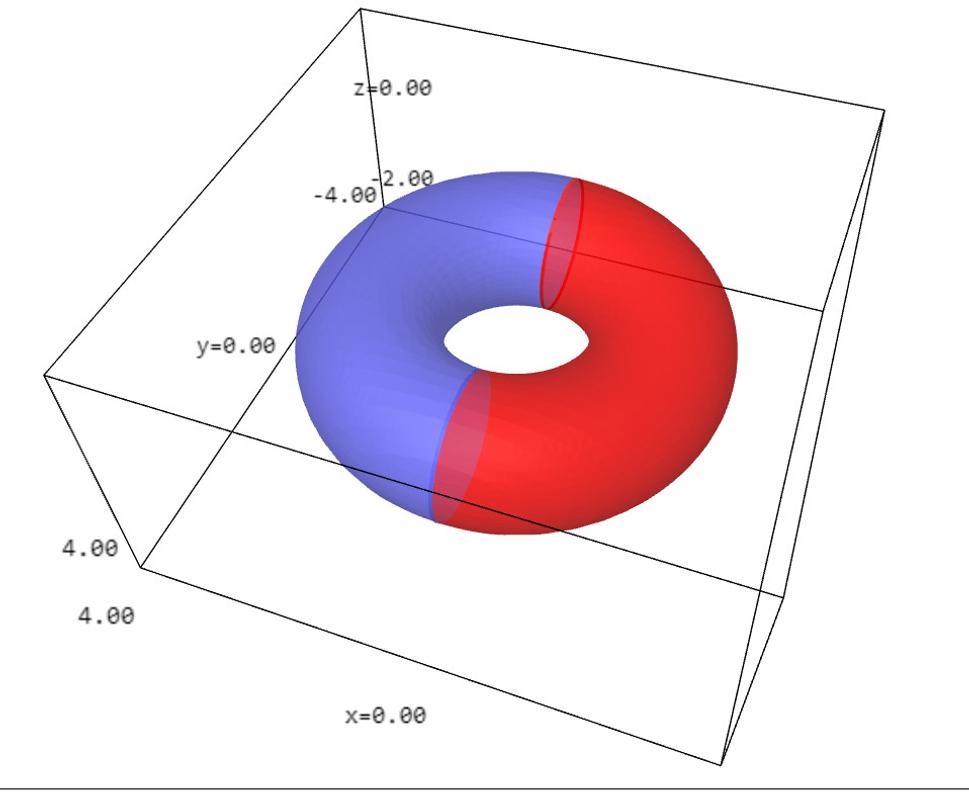
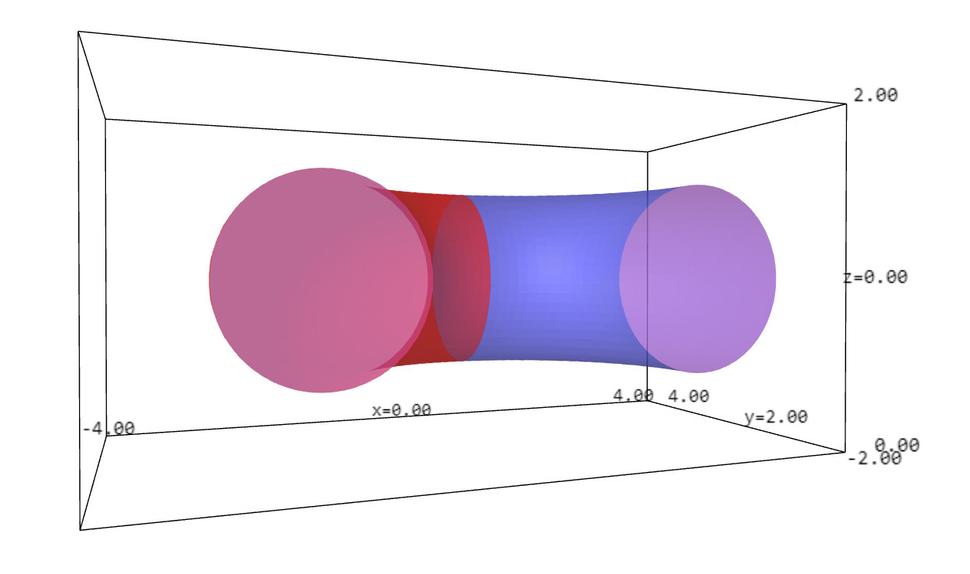
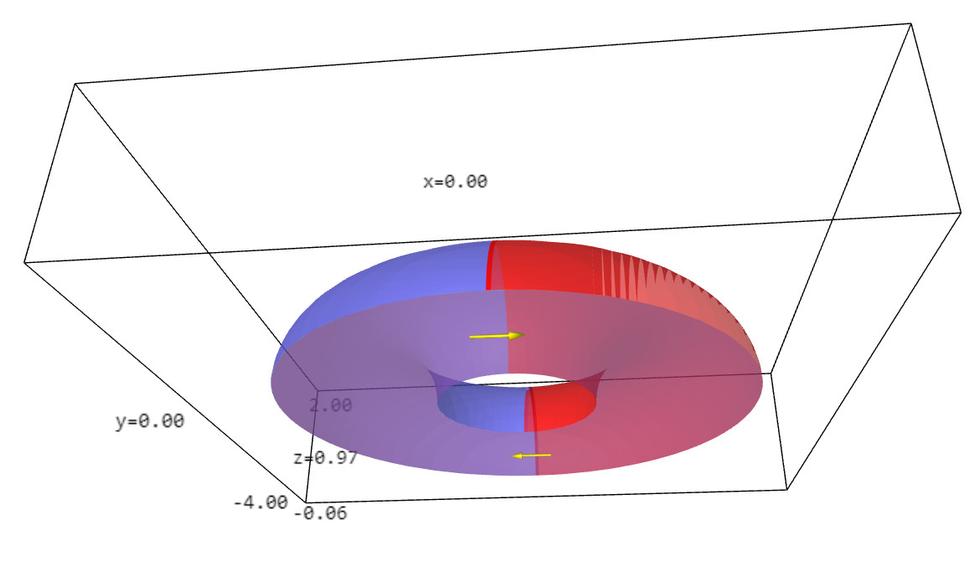
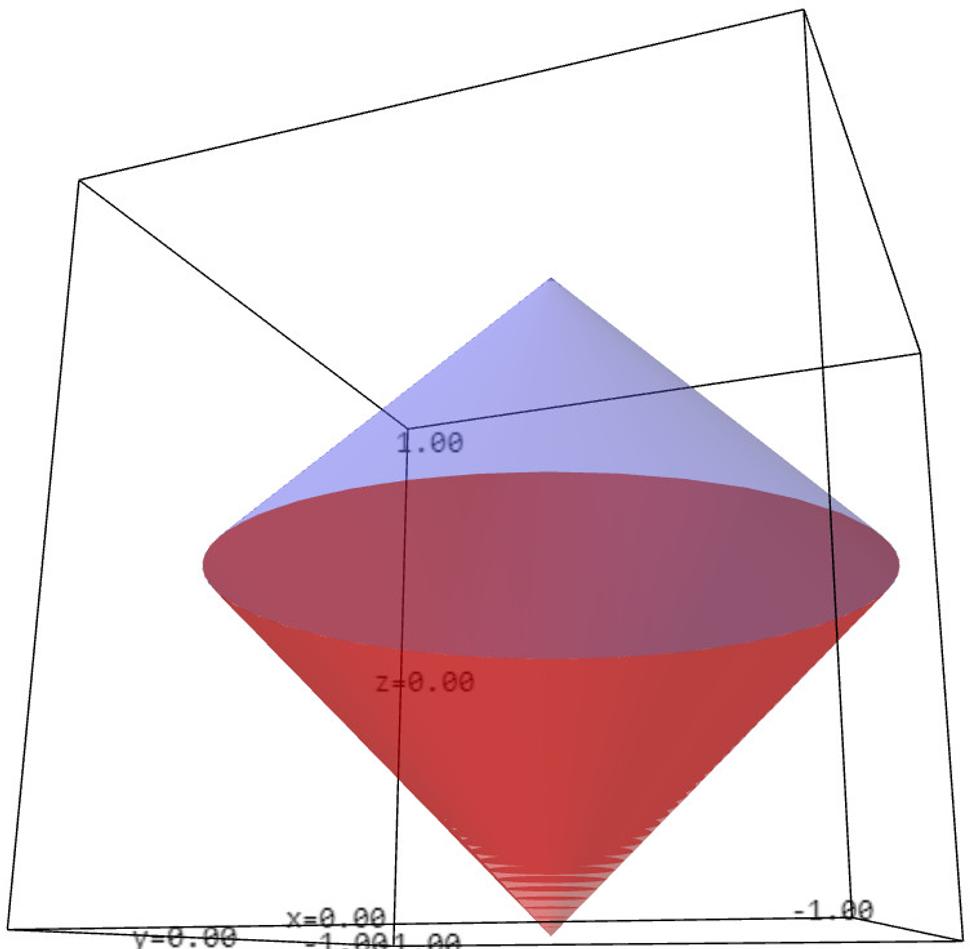
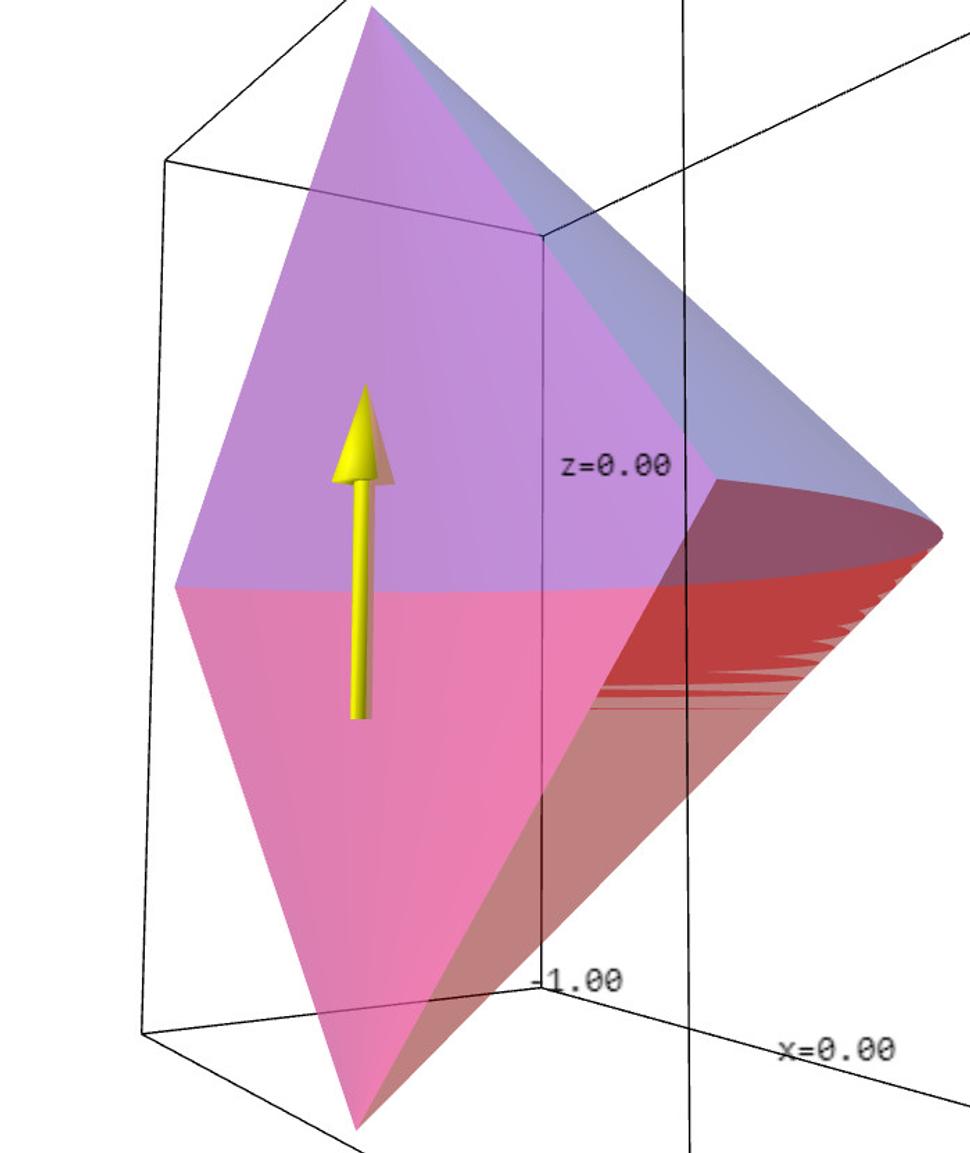
Poďme teraz nakoniec do toho nášho štvorrozmerného vesmíru, kde sú tri priestorové súradnice a jedna časová. Nuž a tu mám zlú správu v tom zmysle, že už nedokážeme nakresliť vôbec nič. Kto chce pochopiť, ako vyzerá náš vesmír v nekonečne, musí sa naučiť matematiku. Mohol by začať s projektívnou geometriou, pretože náš štvorrozmerný zavinutý vesmír pravdepodobne vyzerá ako projektívna kvadrika typu (4,2).



























